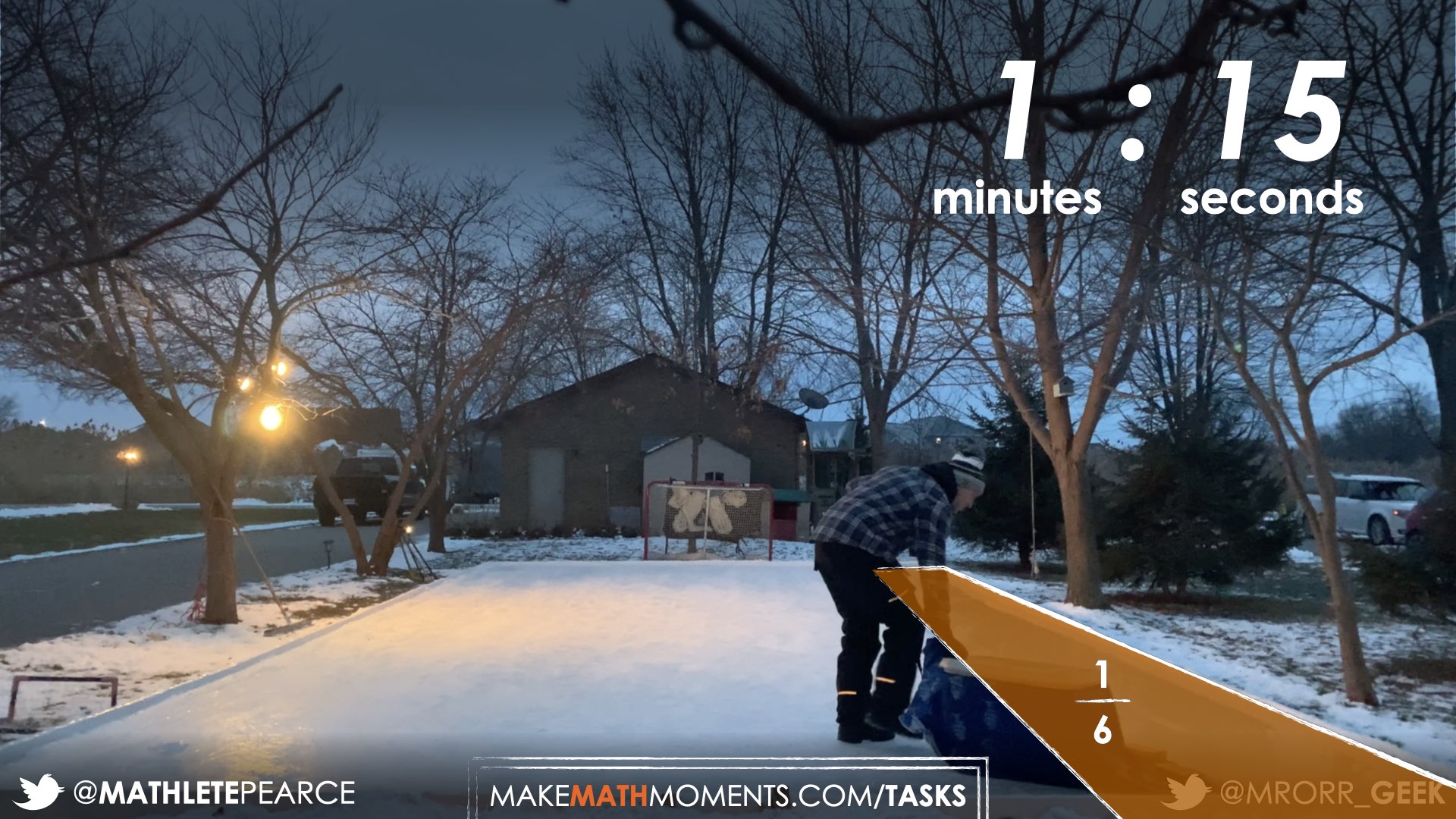Students will determine the fraction of the rink surface flooded. They will also determine the length of time required to flood that fraction of the ice by scaling a ratio in tandem (surface of the rink : time).

In this task, students observe a backyard rink being flooded. Similar to the context in day one, animations will reveal how he went about flooding the ice, in three distinct sections. Today’s task will add a second variable, time. We will investigate the relationship between the surface of the ice flooded, and the time it takes to complete that section. This ratio will allow students to determine the length of time needed to surface different fractional amounts of the rink surface by scaling the ratio in tandem.

Today’s lesson serves to reinforce some of the following big ideas:

• Multiplication can be interpreted as “groups of” or “parts of”, where the first factor is the number of groups, and the second factor is the quota;
• Multiplication can be represented using an array or area model;
• A part of a whole unit can be expressed as a fraction;
• A fraction described the number of parts relative to a whole;
• The fractional unit (the denominator) communicates how the whole is partitioned (number of parts);
• Equivalent values can be represented by different fractional notation (for example, \(\frac{1}{4}\) is equal to \(\frac{3}{12}\));
• The product when multiplying fractions is relative to the whole unit;
• Ratio reasoning is when the units represented by a ratio are scaled in tandem

Show students the following video:

Then, ask students:

What do you notice?

What do you wonder?

Give students 60 seconds (or more) to do a rapid write on a piece of paper.

Replaying the video and/or leaving a screenshot from the video up can be helpful here.

Then, ask students to share with their neighbours for another 60 seconds.

Finally, allow students to share with the entire group. Be sure to write down these noticings and wonderings on the blackboard/whiteboard, chart paper, or some other means to ensure students know that their voice is acknowledged and appreciated.

Some of the noticing and wondering that may come up might include:

• It looks like he’s pulling a cooler.
• Why are we watching this?
• It doesn’t look like the same house as we saw on day 1 when they were shovelling snow.
• I see an ice rink.
• It doesn’t look like the guy who was shovelling snow the other day.
• Is he draining water on the ice?
• It’s like a home-made Zamboni (ice resurfacing machine).
• And many more…

At this point, you can answer any wonders that you can cross off the list right away. For example:

• You’re right – this is not the same man who was shovelling the driveway on Day 1 of this unit, but he is also a teacher; a high school physics teacher.
• This is a different house, but located in the same town only a few kilometres away from the first house.
• It absolutely is a homemade Zamboni. What he does is he fills up the cooler with warm water from in the house, opens the drain out the back and drags a towel with a couple of bricks on it to melt down the top layer of the ice and leave it fresh and smooth.

After we have heard students and demonstrated that we value their voice, we can land on the first questions we will challenge them with:

How much of the skating rink did he flood?

How long do you think it took to flood that section of the ice rink?

Make an estimate.

We can now ask students to make an estimate (not a guess) as we want them to be as strategic as they can possibly be. This will force them to determine a fraction of the skating rink that would be reasonable before determining a more precise answer. Consider asking students to think about an estimate that would be “too low” and an estimate that would be “too high” before asking for their best estimate in order to help them come up with a more reasonable estimate. Encourage students to share their estimates, however avoid sharing their justification just yet. We do not want to rob other students of their thinking.

Facilitator Note:

The prompt intentionally omitted the word “fraction”. Although based on the lesson from Day 1, it is likely that many students will describe the area of the surface using fractional language.

Show the following video clip revealing that one-sixth of the skating rink has been flooded, and therefore he still has five-sixths of the rink that has not been flooded yet. You’ll also notice that it took approximately 1 minute and 15 seconds to flood the one-sixth section of the ice.

Celebrate student estimates that were very close to actual using a routine of your choice as we head into the sense making portion of this lesson.

Share the following video that shows the second section of the rink being flooded; this time, in horizontal strips.

Prompt students by stating:

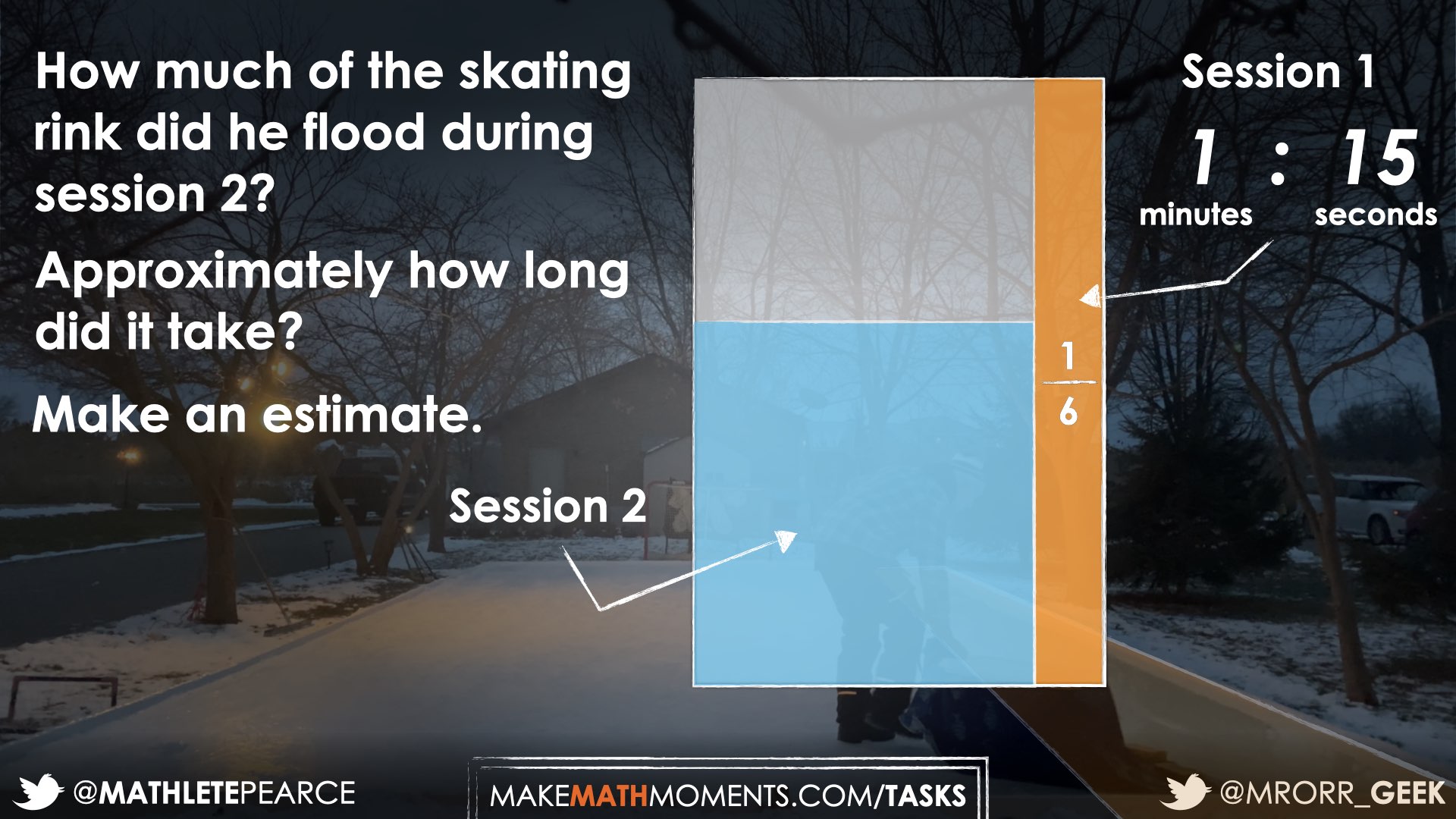
What fraction of the whole rink was flooded during the second session of the process?

How long should it take to flood this section?

Estimate.

Be sure to elaborate to students that we want them to estimate what fraction of the whole rink Session 2 (shaded in blue) represents not how much of the remaining 5 sixths of the ice that had not been flooded during Session 1.

You might consider jotting these estimates on a number line and attaching student names to their estimates and ask them to share their reasoning.

Then, you can reveal to students that:

Approximately 3 fifths of the 5 sixths section of the rink that was not flooded during the first session was flooded during the second session.

Approximately what fraction of the whole rink was flooded during the second session?

About how long should it take to flood this section?

Facilitator Note:

Clarify, if needed, that you want students to determine the amount flooded in the second video only relative to the whole ice rink (not the cumulative amount from both the first and second video).

Be sure to remind students that they are not to use a calculator and that they are to convince their mathematics community using mathematical models.

If students are struggling with the language, you might consider sharing this animated gif to highlight what “3 fifths of 5 sixths of the remaining unflooded section of ice” really means.

Login/Join to access the entire Teacher Guide, downloadable slide decks and printable handouts for this lesson and all problem based units.

Login/Join to access the entire Teacher Guide, downloadable slide decks and printable handouts for this lesson and all problem based units.

Login/Join to access the entire Teacher Guide, downloadable slide decks and printable handouts for this lesson and all problem based units.

Login/Join to access the entire Teacher Guide, downloadable slide decks and printable handouts for this lesson and all problem based units.

Login/Join to access the entire Teacher Guide, downloadable slide decks and printable handouts for this lesson and all problem based units.

After consolidating this lesson using student generated solution approaches and you’ve made connections across those strategies and models, share the following reveal video.

Here’s the final frame from the silent solution reveal video.

Students will complete the following task and reflection independently. 

Consolidation Prompt #1:

Login/Join to access the entire Teacher Guide, downloadable slide decks and printable handouts for this lesson and all problem based units.

We suggest collecting this reflection as an additional opportunity to engage in the formative assessment process to inform next steps for individual students as well as how the whole class will proceed.

Download Editable/Printable Handout

Become a member to access purposeful practice to display via your projector/TV, download the PDF to upload to your LMS and/or print for students to have a physical copy

JOIN TO DOWNLOAD