SHOT PUT [DAY 6]
EQUIVALENCE AND ALGEBRAIC SUBSTITUTION
Student will explore solving equations using the idea of equivalence and substitution.
Intentionality
Math Talk
Spark Curiosity
During Moves
Student Approaches
Next Moves
Consolidation
Reflect and Consolidation Prompts
Resources & Downloads
Educator Discussion Area
Intentionality & Unit Overview
Length of Unit: 6 Days
Access each lesson from this unit using the navigation links below
Students will explore solving equations using the idea of equivalence and substitution.
Intentionality…
Today, students will have an opportunity to reason through an investigation extending the shot put context. Again, the tasks involve measuring different shot put throws with two different length measuring sticks. However, in this scenario, the total length of each throw and length of each measuring stick is known, but the number of measuring sticks is unknown allows students to solve a two-variable system of linear equations using mathematical models such as the number line and/or double number line.
This scenario builds off of our day 2 understanding of quotative division meaning the length of each stick (i.e.: rate or quota) is known and the number of sticks (i.e.: parts) is unknown. Recall from yesterday that we were trying to determine the length of each measuring stick, whereas today we will be trying to find the number of sticks instead. Again, although we are not necessarily using quotative division, the big ideas are still prevalent.
They will also explore big ideas including the following:
- There are two types of division; partitive and quotative.
- Each side of an equation can be thought of as a single unit, where both sides are equivalent.
- Quantities can be reassociated to create new units that can be substituted for equivalent quantities.
- A multiple of one quantity can be equivalent to a multiple of another quantity which can be used to substitute.
- The algebraic strategy of substitution can assist in solving for unknown quantities in an equation.
Math Talk
Related String Of Problems
First Shot Put Throw: Problem #1
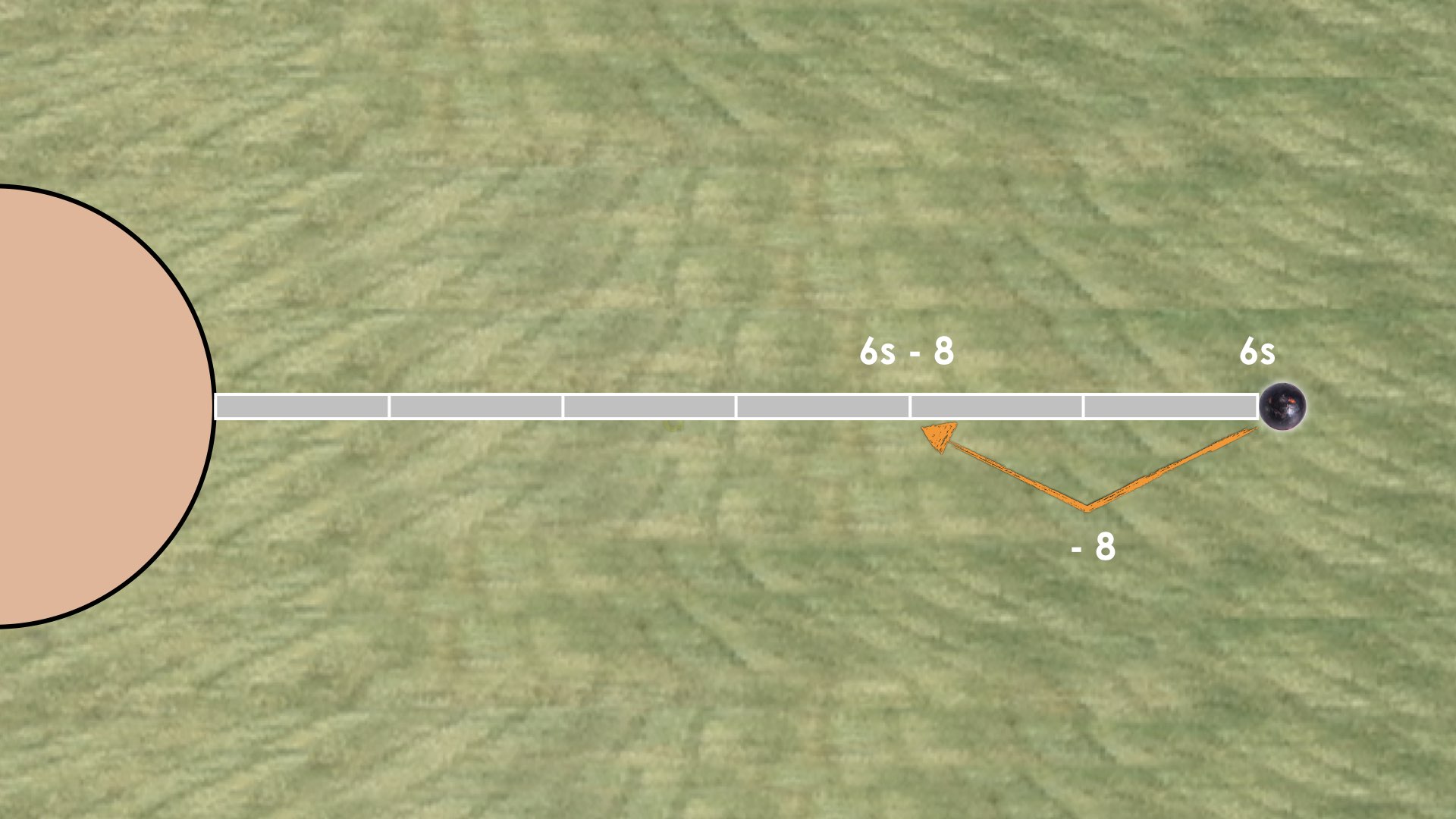
The officials say that 6 measuring sticks were used to measure a throw. Represent this scenario on a number line.
First Shot Put Throw: Problem #2
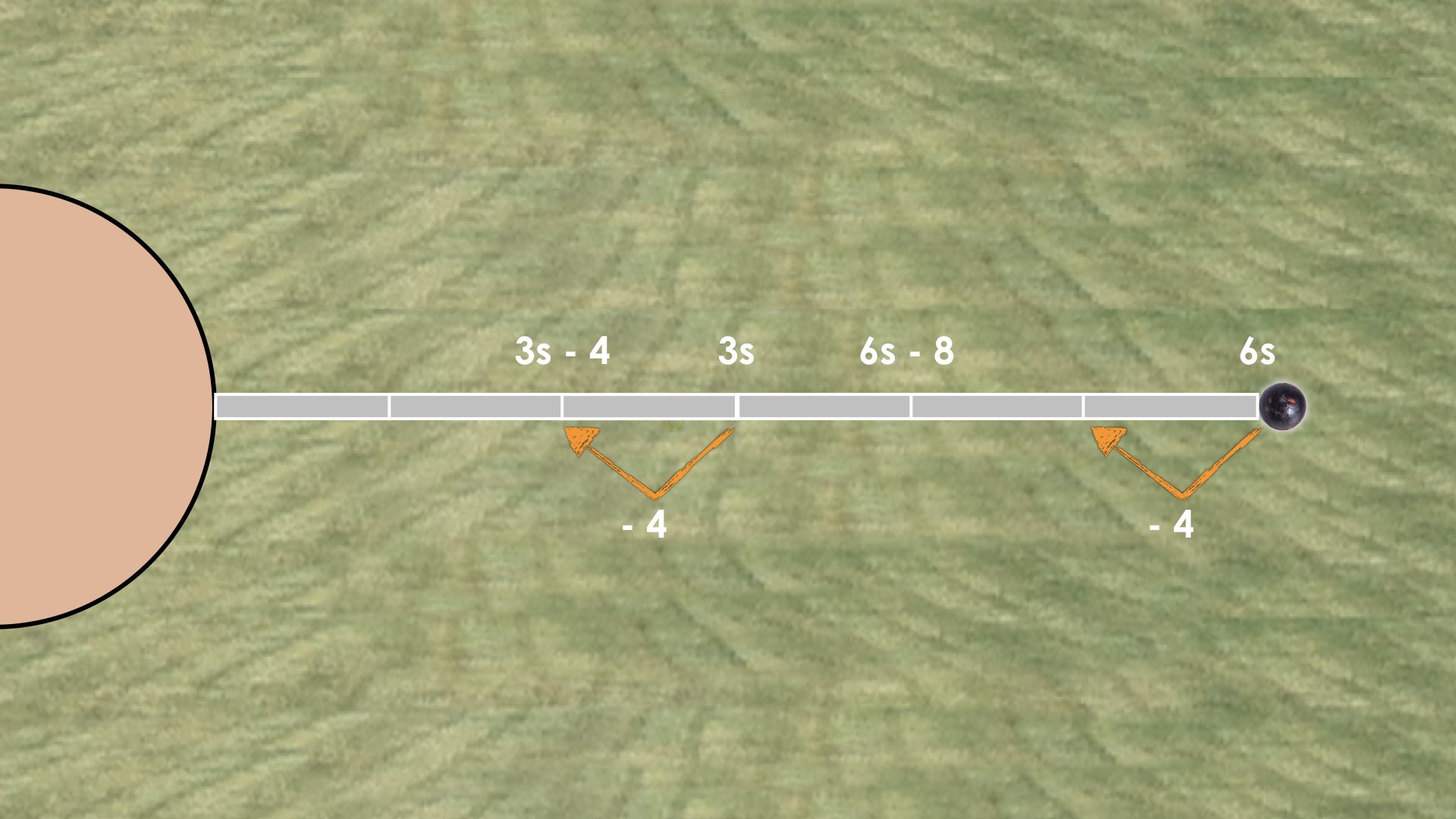
We know that 6 measuring sticks minus 8 feet is equal to 4 measuring sticks. Represent this scenario on the number line.
First Shot Put Throw: Problem #3
How about 3 measuring sticks minus 4 feet? Where would that go? Why?
A second shot put was thrown and…
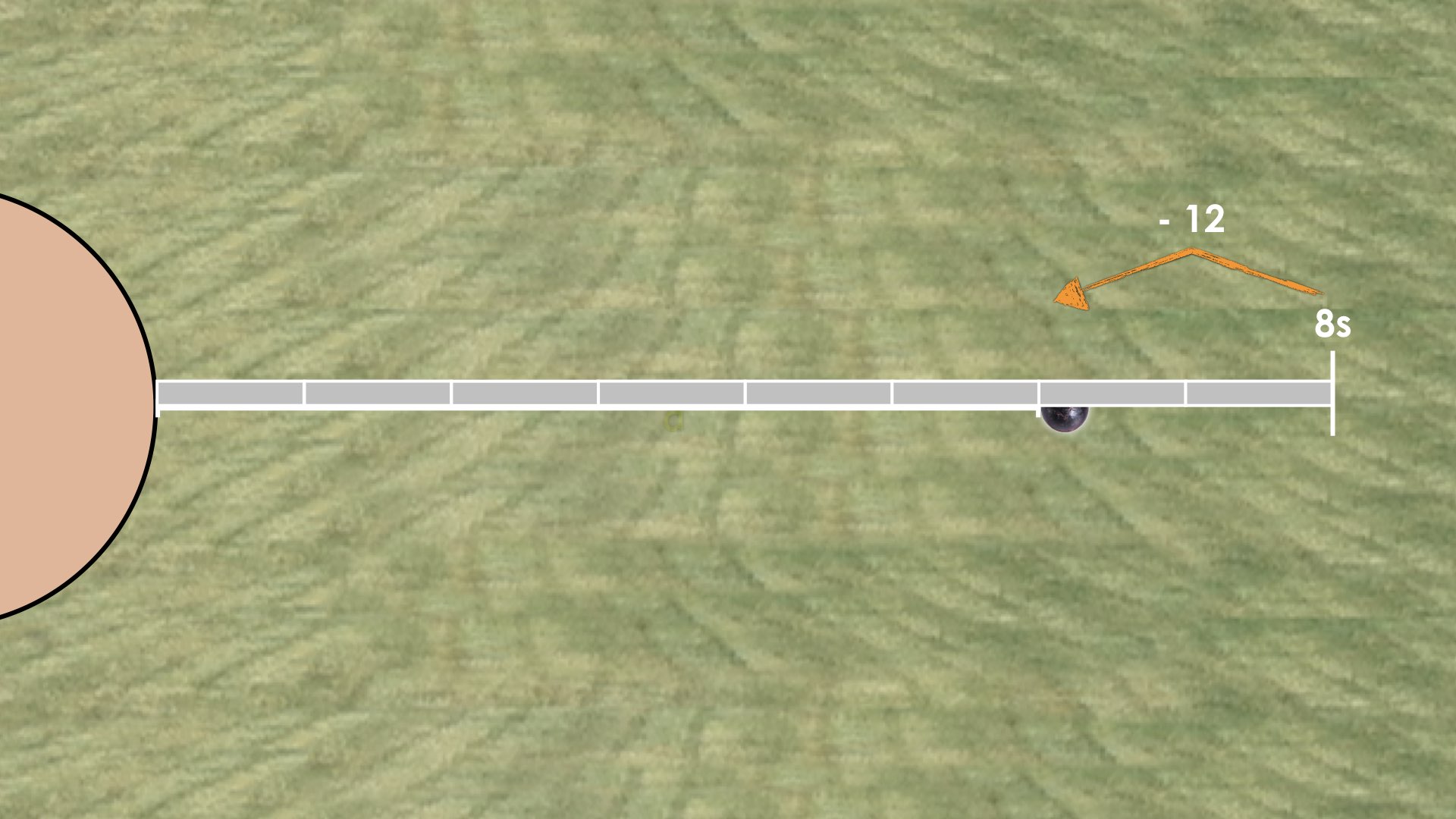
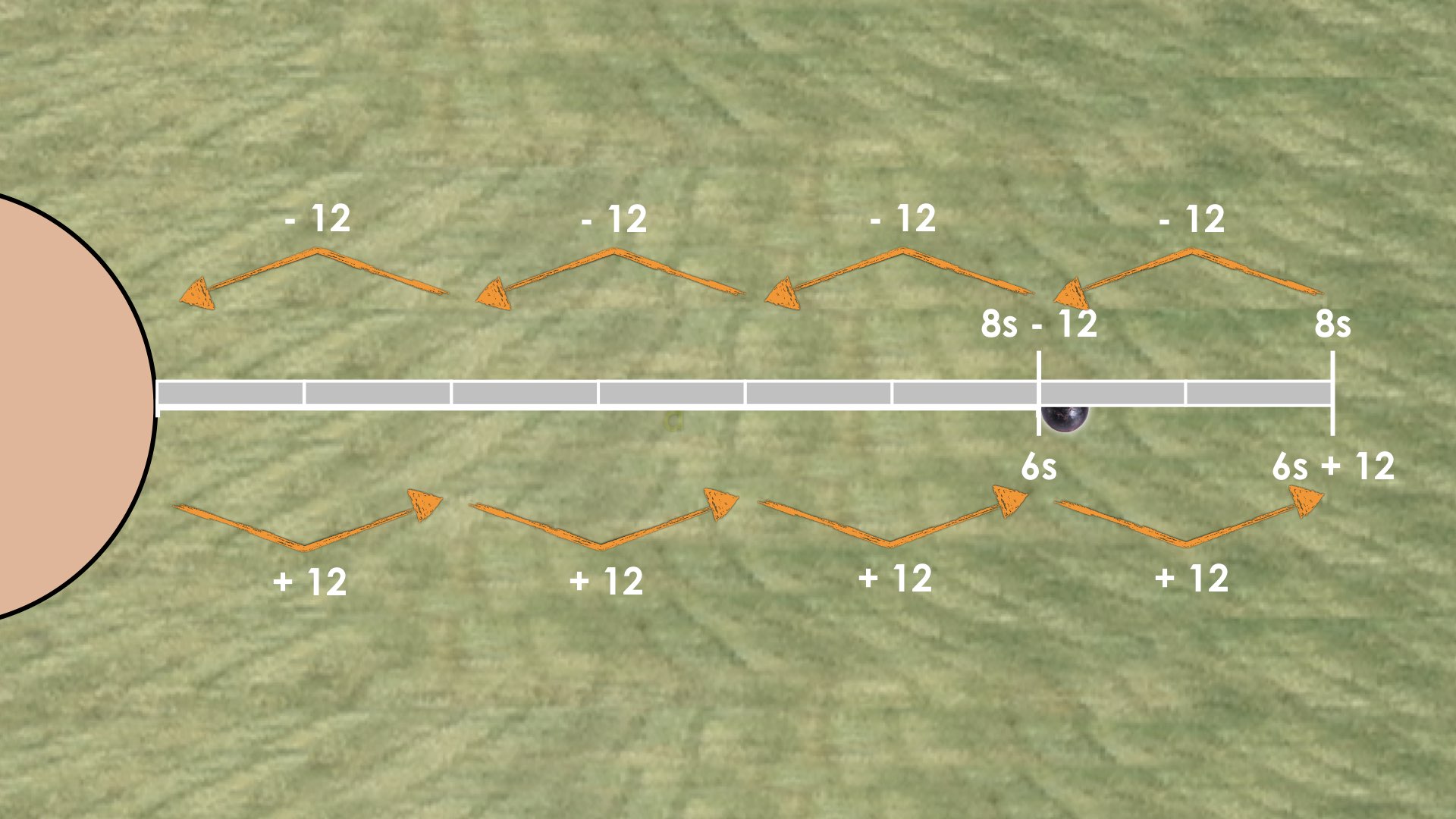
… one official used 8 measuring sticks minus 12 feet to measure the throw exactly.
Another official used 6 of the same length measuring sticks to measure the throw exactly.
How long would each of these measuring sticks be?
A third shot put was thrown and…
…one official used 7 measuring sticks plus 18 feet to measure the throw exactly.
Another official used 9 of the same length measuring sticks to measure the throw exactly.
How long would each of these measuring sticks be?
Consider modelling student thinking on the double number line
Walk Through Video
Facilitator Notes
In this string of related problems, we will be providing students with an opportunity to use the double number line as a tool to solve multi-step single variable equations where two equivalent expressions are given.
For the First Shot Put Throw: Problem #1, we know that a throw was measured with exactly 6 measuring sticks. The goal here is to give students a very low floor to start this math talk and have them model what that looks like on a number line using 6 jumps or 6 bars to represent the total distance of the throw.
From here, we build on this first problem by stating First Shot Put Throw: Problem #2 mentioning that if you move 8 feet backwards, you’ll be at the same distance as 4 of the same measuring sticks.
This should be immediately helpful to many students as some might quickly come to realize that if moving back 8 feet from the distance of 6 measuring sticks will bring you to the distance of 4 measuring sticks, then 2 measuring sticks have a length of 8 feet.
If 2 measuring sticks have a length of 8 feet, then 1 measuring stick must have a length of 4 feet.
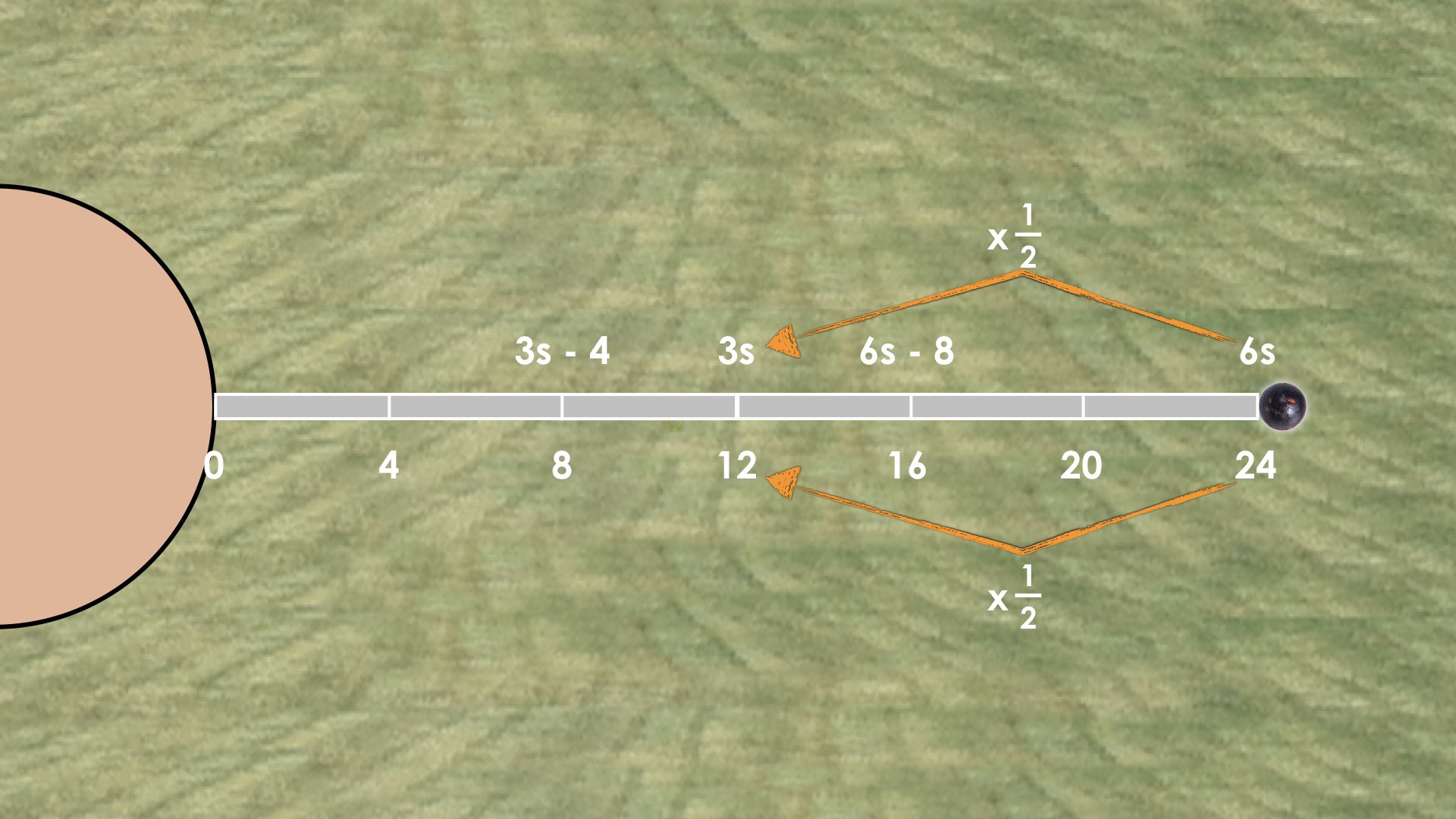
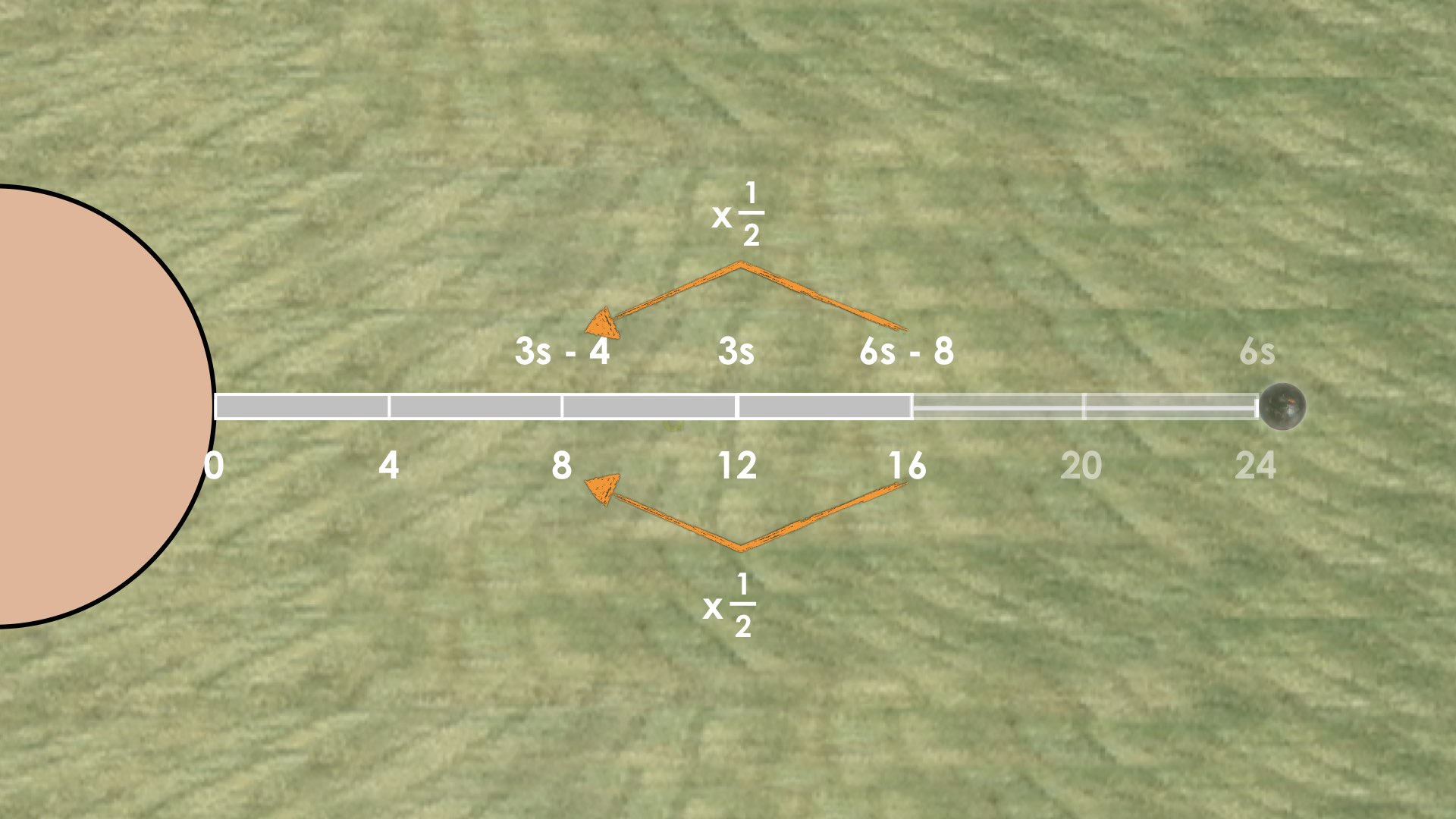
We then present First Shot Put Throw: Problem #3 which asks students to determine where they would place 3 sticks less 4 feet on the number line. This related problem is crafted specifically to elicit the opportunity for students to utilize scaling in tandem. If students are able to recognize that 3s – 4 is half of 6s – 8, then we can simply half those quantities and half the distance on the number line to come to the conclusion that 3s – 4 must be the same distance as 2 measuring sticks.
Some students may not recognize the opportunity for scaling in tandem, but rather use the fact that they learned in the previous problems that each measuring stick had a length of 4 feet. While we do not want to funnel students away from their own thinking and approach to tackling these problems, we do want to ensure that we highlight this idea explicitly as you model student thinking.
More scaling in tandem in action:
In the second shot put throw, students are given another opportunity to wrestle with this idea of algebraic thinking through substitution as well as scaling in tandem. This time, 8 measuring sticks extend 12 feet beyond the shot put landing spot. However, we know that the throw measures exactly 6 measuring sticks in length.
These equivalent expressions provide students more opportunity to work with algebraic reasoning and in particular, the algebraic big idea of substitution and a big idea from proportional reasoning we’ve developed along the way called scaling in tandem.
The third shot put throw may be helpful, however use your judgement to determine whether the third throw is necessary or whether it might be saved for further investigation and/or purposeful practice on another day.
Sense Making
Crafting The Productive Struggle: Prompt
Pose the following question:A shot put that was thrown a distance of 78 feet was measured with orange and purple measuring sticks. Recall, each orange measuring stick has a length of 9 feet, while each purple measuring stick has a length of 6 feet. A total of 10 measuring sticks were used to measure the throw. Determine the number of orange and number of purple measuring sticks that were used to measure this distance exactly.
Walk Through Video
Facilitator Notes
Students are strongly encouraged to model this scenario using a number line and/or using concrete manipulatives such as relational rods to create a linear model. We have included a BLM with 10 copies of each measuring stick that students might consider cutting out and using to build a model. You can download the Shot Put Day 6 BLM – Measuring Sticks handout in PDF form here [ OPEN | DOWNLOAD ] or in the resources section.
Some students might use a guess and check strategy. Those who do, tend to start with all 10 measuring sticks of one colour and determining whether that will work or need to be adjusted by swapping out one stick at a time for a stick of the other colour.
In particular, many students may begin by randomly trying combinations of purple measuring sticks and orange measuring sticks. At some point, some students may begin with all purple or all orange measuring sticks and trying to “adjust” through substitution until they reach 78 feet total.
For example, a student who starts with all purple measuring sticks will make it to 60 feet in length.
From here, they can systematically “swap” or substitute 1 orange for 1 purple with the result being a gain of 3 feet for each substitution.
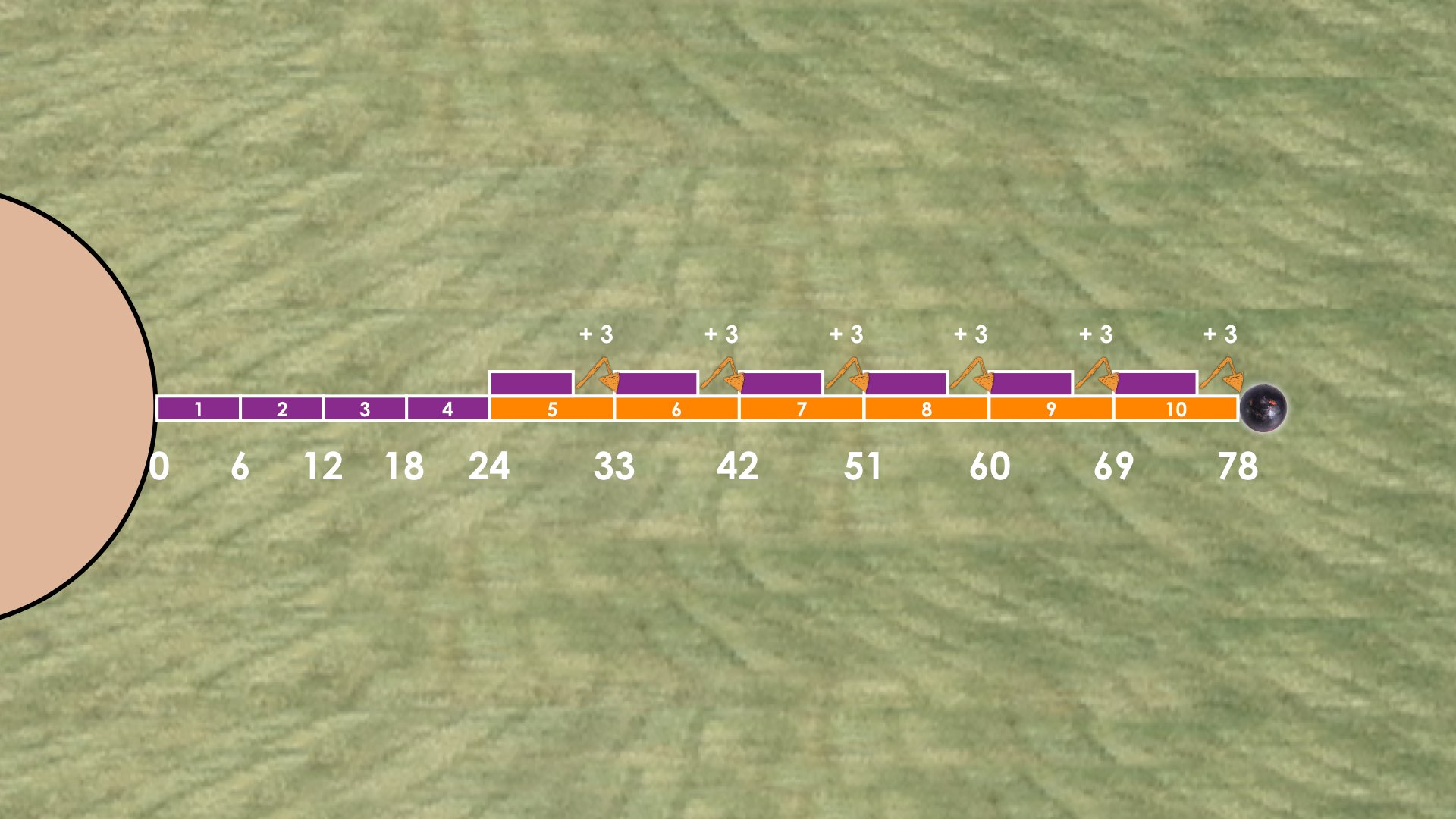This gain of 3 feet is extremely important when we consider what is happening when we symbolically represent this scenario as a linear system of equations and begin substituting with equations. While the above image can be achieved through trial and error or guess and check, some students may land on the idea that 10 purple measuring sticks leaves us 18 feet short of the shot put landing spot.
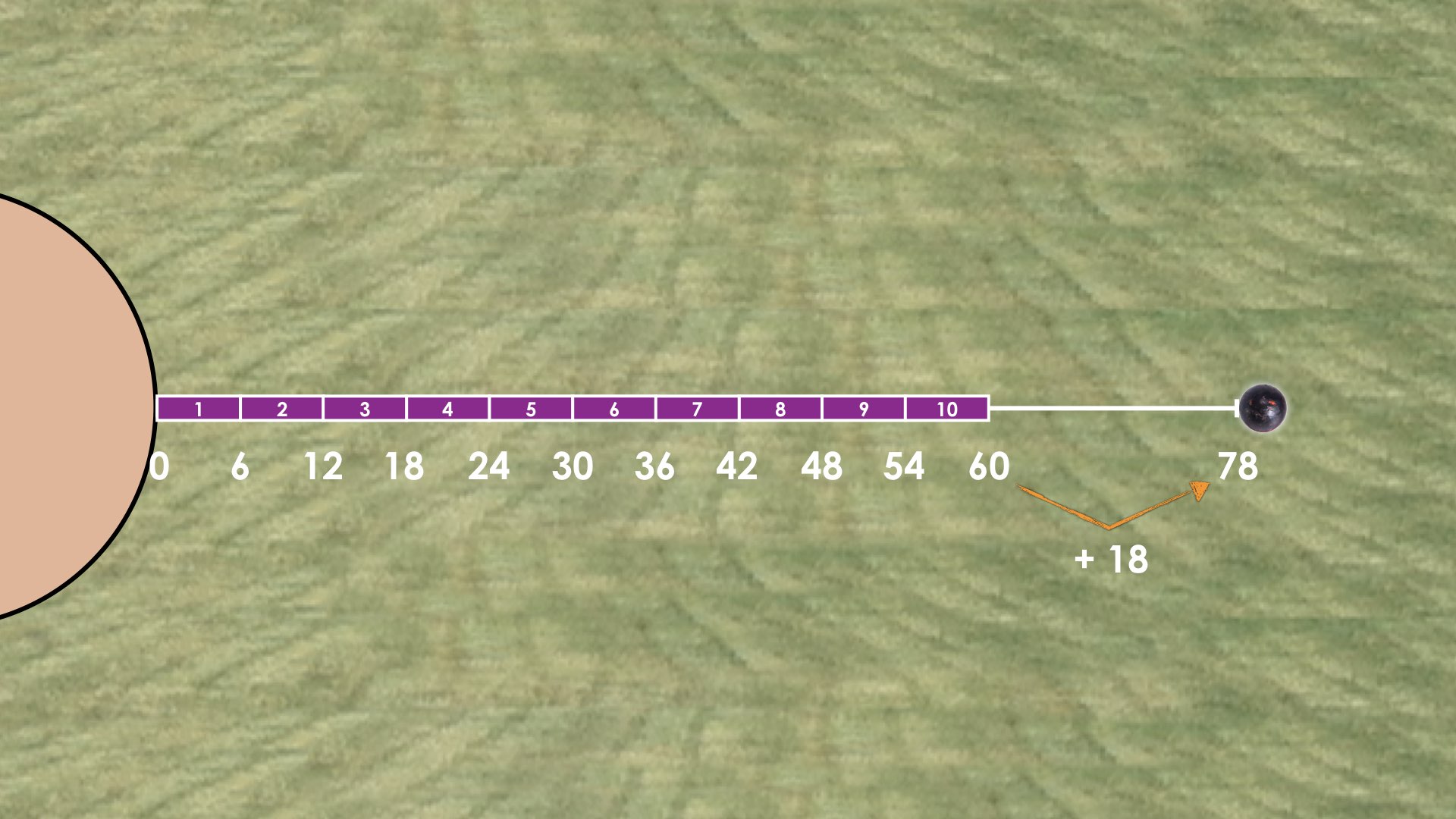Since each orange stick is 3 feet longer than a purple stick, I gain 3 feet for each orange stick for purple stick substitution. That means that I can find the number of required orange sticks by determining how many 3 foot units I need to reach 78 feet from the current length of 60 feet.
Both of these visual approaches are extremely helpful for making a connection to the symbolic approach of solving a linear system of equations with substitution.
In particular, for the student who started with all purple measuring sticks on the number line, that is conceptually equivalent to substituting 10 – o as the number of p (purple measuring sticks).
Substituting 10 – o for p in the equation 6p + 9o = 78 leverages the idea that if we start with 10 purple measuring sticks or 60 feet, that we’ll need to subtract 6 feet and add 9 feet for every orange measuring stick to land at a total distance of 78 feet.
This can be shown both visually and symbolically like this:
This symbolic approach of starting with 10 purple sticks and 60 feet of length, then repeatedly removing 6 feet and adding back 9 feet for each purple stick being replaced with an orange stick can be summarized as removing 6 feet, 6 times and adding 9 feet, 6 times or removing 36 feet and adding back 54 feet to reach a total of 78 feet.
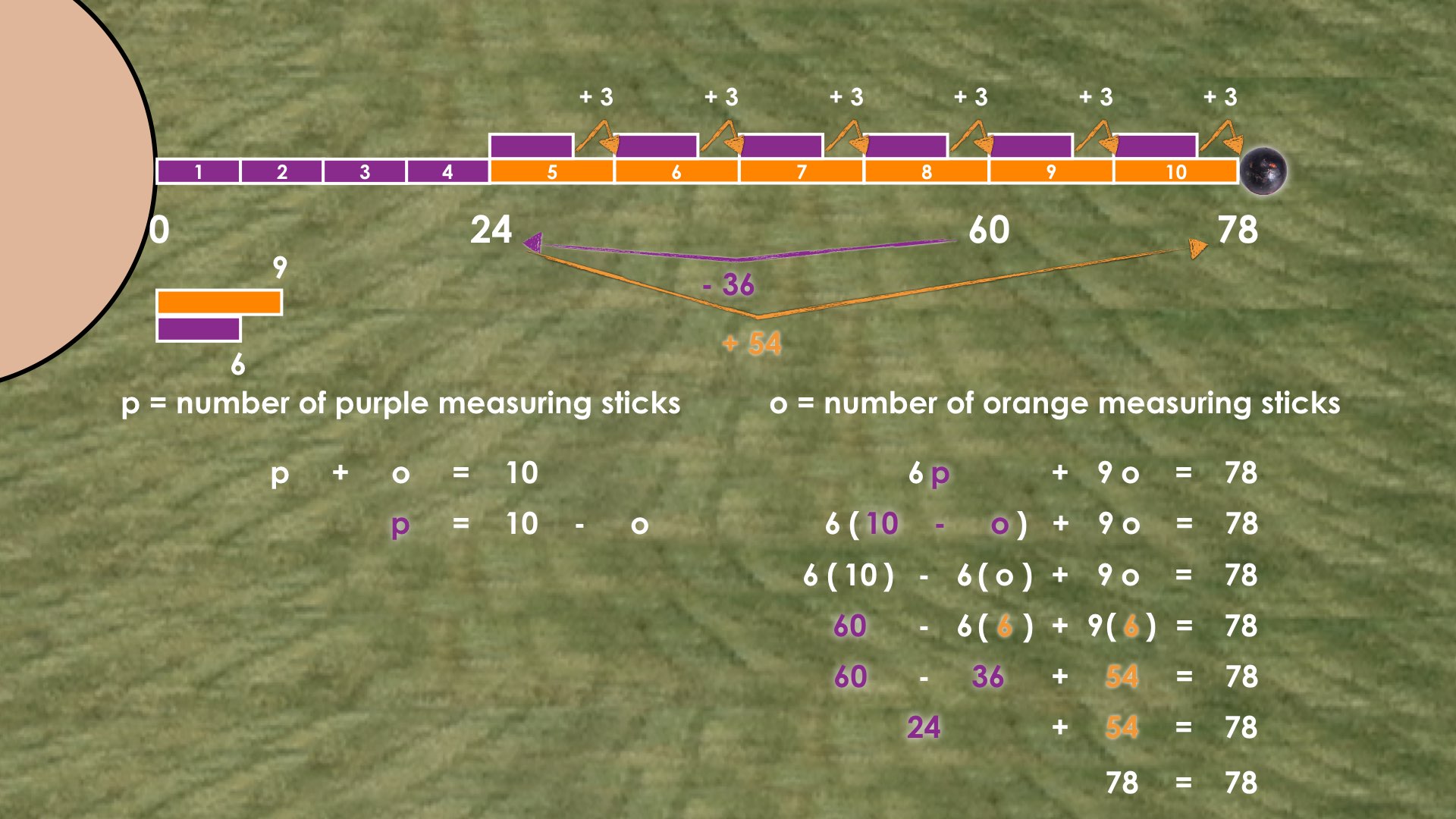Alternatively, we can leverage the second visual approach of considering the remaining 18 feet required to increase our current distance of 60 feet to our total throw distance of 78 feet. This visual approach we shared earlier is conceptually equivalent to removing 60 feet from both sides of the equation and simplifying -6o and +9o to show that 3o is equivalent to 18 feet. In other words, we are asking how many chunks or parts of 3 feet are needed to reach 18 feet?
Using quotative division, we can determine that there are 6 parts of 3 feet needed to reach 18 feet.
Therefore, the number of orange measuring sticks is 6.
From here, we can use either of our equations or the visual model to determine that the number of purple measuring sticks must be 4. During Moves
While Students Are Productively Struggling…
Login/Join to access the entire Teacher Guide, downloadable slide decks and printable handouts for this lesson and all problem based units.
Student Approaches
Student Approach #1: Concrete Bar Model Using Guess and Check
Login/Join to access the entire Teacher Guide, downloadable slide decks and printable handouts for this lesson and all problem based units.
Student Approach #2: Number Line Using Substitution
Login/Join to access the entire Teacher Guide, downloadable slide decks and printable handouts for this lesson and all problem based units.
Student Approach #3: Array Model Using Substitution
Login/Join to access the entire Teacher Guide, downloadable slide decks and printable handouts for this lesson and all problem based units.
Next Moves
Reveal
After consolidating learning using student generated solution strategies and by extending their thinking intentionally, we can share what really happened by showing the following video/image revealing the length of the teal measuring stick and length of the throw.
Show the silent solution video and/or images below demonstrating some possible visual approaches to solving this problem:
Visual Approaches: Silent Solution Video
Visual Approaches: Image #2
If your students are ready to represent their thinking symbolically, you might consider using the silent solution video and/or images below to model some symbolic approaches to solving this problem:
Symbolic Approaches: Silent Solution Video
Symbolic Approaches: Image #1
Symbolic Approaches: Image #2
Answers: The official used 6 orange measuring sticks and 4 purple measuring sticks.
Revisit the student answers.
Consolidation
Login/Join to access the entire Teacher Guide, downloadable slide decks and printable handouts for this lesson and all problem based units.
Reflect and Consolidation Prompts
Provide students an opportunity to reflect on their learning by offering this consolidation prompt to be completed independently.
Consolidation Prompt #1:
Login/Join to access the entire Teacher Guide, downloadable slide decks and printable handouts for this lesson and all problem based units.
Consolidation Prompt #2:
Login/Join to access the entire Teacher Guide, downloadable slide decks and printable handouts for this lesson and all problem based units.
We suggest collecting this reflection as an additional opportunity to engage in the formative assessment process to inform next steps for individual students as well as how the whole class will proceed.
Resources & Downloads
Login/Join to access the entire Teacher Guide, downloadable slide decks and printable handouts for this lesson and all problem based units.
Printable Lesson Plan PDF
Videos, Images & Media Files
Apple Keynote Presentation
Powerpoint Presentation
Printable Consolidation Prompts
Educator Discussion Area
Login/Join to access the entire Teacher Guide, downloadable slide decks and printable handouts for this lesson and all problem based units.
Explore Our 60+ Problem Based Units
This Make Math Moments Lesson was designed to spark curiosity for a multi-day unit of study with built in purposeful practice, number talks and extensions to elicit and emerge strategies and mathematical models.
Dig into our other units of study and view by concept continuum, grade or topic!
