Students will explore solving equations using the idea of equivalence and substitution.

Today, students will have an opportunity to reason through an investigation extending the shot put context. Again, the tasks involve measuring different shot put throws with two different length measuring sticks. However, in this scenario, the total length of each throw and length of each measuring stick is known, but the number of measuring sticks is unknown allows students to solve a two-variable system of linear equations using mathematical models such as the number line and/or double number line.

This scenario builds off of our day 2 understanding of quotative division meaning the length of each stick (i.e.: rate or quota) is known and the number of sticks (i.e.: parts) is unknown. Recall from yesterday that we were trying to determine the length of each measuring stick, whereas today we will be trying to find the number of sticks instead. Again, although we are not necessarily using quotative division, the big ideas are still prevalent.

They will also explore big ideas including the following:

• There are two types of division; partitive and quotative.
• Each side of an equation can be thought of as a single unit, where both sides are equivalent.
• Quantities can be reassociated to create new units that can be substituted for equivalent quantities.
• A multiple of one quantity can be equivalent to a multiple of another quantity which can be used to substitute.
• The algebraic strategy of substitution can assist in solving for unknown quantities in an equation.

In today’s string, students will substitute different units of small and large bags of chocolate candies with total given quantities.

Set the context:

There are two sizes of chocolate candy packages; small and large.

How many chocolate candies come in a small package and how many come in a large package when…

Problem #1:

… you combine 1 small and 1 large package the total is 15 and when you combine 3 small packages and 4 large packages the total is 54?

Problem #2:

… you combine 3 small and 4 large packages the total is 47 and when you combine 3 small packages and 1 large package the total is 23?

Problem #3:

… you combine 5 small and 2 large packages the total is 61 and when you combine 2 small packages and 2 large packages the total is 40.

Consider modelling student thinking on a number line.

If you’d like to see how you might model a portion of this math talk, consider viewing this walk-through video.

In today’s math talk, we will provide students with the opportunity to reinforce the algebraic strategy of substitution as revealed through the day 3 task. You will recall that on day 3, students substituted 1 green measuring stick and 1 black measuring stick with a length of 15 feet.

Today, students will substitute different units of small and large bags of chocolate candies with total given quantities.

Big Idea:

The big idea we hope to reveal through this math talk is unitizing quantities in order to substitute and solve for unknown quantities.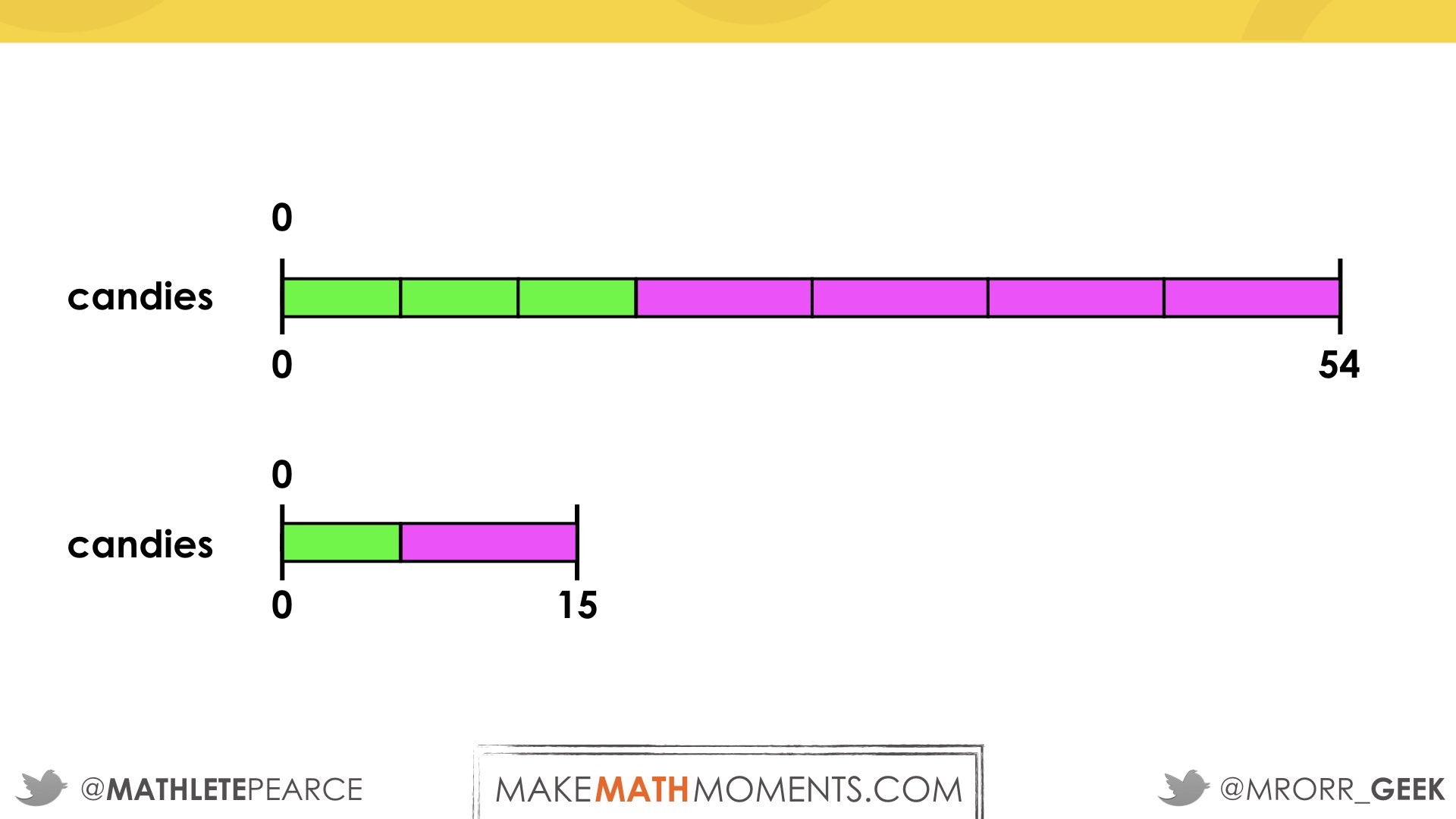

Use your professional judgement to determine whether students are still at the concrete or visual stage for applying the algebraic idea of substitution by systematically “swapping” every unit of 1 small package (modelled in green) and 1 large package (modelled in pink) for a quantity of 15 candies or whether they are ready to begin connecting the visual representation to a symbolic representation.

If you’d like to see how you might facilitate this portion of the lesson, consider viewing this walk-through video.

Pose the following question:

A shot put was thrown and landed at a distance of 84 feet; a new record! 

The officials can measure the throw using green measuring sticks that are 8 feet long or blue measuring sticks that are 12 feet long. 

What are all of the possible ways that the officials could use these measuring sticks to confirm the length of the throw?

After students have had some time to ponder prompt #1, share prompt #2:

Another shot put was thrown and landed at a distance of 80 feet. While the officials will be measuring using 8 foot green measuring sticks and 12 foot blue measuring sticks, they only have access to 5 green measuring sticks.

How many of each measuring stick must they use to measure the 80 foot shot put throw exactly?

As students are working, encourage them to model the different combinations of green and blue measuring sticks by modelling the scenarios. A number line may be a helpful suggestion, however be sure not to funnel student thinking too forcefully.

Consider asking students purposeful questions that will encourage students to consider the relationship between the green and blue measuring sticks. For example, on day 2, students realized that for the length of every 2 orange measuring sticks, they could be substituted with 3 purple measuring sticks to cover the same distance. Ask students whether they believe that thinking might be helpful here?

Login/Join to access the entire Teacher Guide, downloadable slide decks and printable handouts for this lesson and all problem based units.

Login/Join to access the entire Teacher Guide, downloadable slide decks and printable handouts for this lesson and all problem based units.

Login/Join to access the entire Teacher Guide, downloadable slide decks and printable handouts for this lesson and all problem based units.

Login/Join to access the entire Teacher Guide, downloadable slide decks and printable handouts for this lesson and all problem based units.

Login/Join to access the entire Teacher Guide, downloadable slide decks and printable handouts for this lesson and all problem based units.

Login/Join to access the entire Teacher Guide, downloadable slide decks and printable handouts for this lesson and all problem based units.

Login/Join to access the entire Teacher Guide, downloadable slide decks and printable handouts for this lesson and all problem based units.

Login/Join to access the entire Teacher Guide, downloadable slide decks and printable handouts for this lesson and all problem based units.

After consolidating learning using student generated solution strategies and by extending their thinking intentionally, we can share what really happened by showing the following video/images revealing the possibilities for Prompts #1 and #2.

Prompt #1 Silent Solution Reveal:

Prompt #1 Answers: 9 green, 1 blue; 6 green, 3 blue; 3 green, 5 blue; 0 green, 7 blue.

Prompt #2 Silent Solution Reveal:

Prompt #2 Answer: 1 green, 6 blue; or, 4 green, 4 blue.

Revisit the student answers.

Provide students an opportunity to reflect on their learning by offering this consolidation prompt to be completed independently.

Consolidation Prompt:

Login/Join to access the entire Teacher Guide, downloadable slide decks and printable handouts for this lesson and all problem based units.

We suggest collecting this reflection as an additional opportunity to engage in the formative assessment process to inform next steps for individual students as well as how the whole class will proceed.

Download Editable/Printable Handout

Become a member to access purposeful practice to display via your projector/TV, download the PDF to upload to your LMS and/or print for students to have a physical copy

JOIN TO DOWNLOAD