SHOT PUT [DAY 2]
EQUIVALENCE AND ALGEBRAIC SUBSTITUTION
Student will explore solving equations using the idea of equivalence and substitution.
Intentionality
Math Talk
Spark Curiosity
Fuel Sensemaking
During Moves
Student Approaches
Next Moves
Consolidation
Reflect and Consolidation Prompts
Resources & Downloads
Educator Discussion Area
Intentionality & Unit Overview

Length of Unit: 6 Days
Access each lesson from this unit using the navigation links below
Students will explore solving equations using the idea of equivalence and substitution.
Intentionality…
Today, students will have an opportunity to reason through an investigation extending the shot put context. The tasks involve exploring two equivalent, single variable equations that help to reveal both types of division: partitive and quotative. Students will have another opportunity to apply models to reason; in particular, the double number line.
They will also explore big ideas including the following:
- There are two types of division; partitive and quotative.
- The commutative property of multiplication impacts the type of division when solving for an unknown factor.
- Each side of an equation can be thought of as a single unit, where both sides are equivalent.
- Changing the quantity on one side of an equation forces an equivalent change in the other.
- A multiple of one quantity can be equivalent to a multiple of another quantity.
Math Talk
Walk Through Video
Watch this “Walk Through” video of the entire math talk portion of the lesson to gain a better understanding of the intentionality behind this string of related problems:String of Related Problems
For today’s Math Talk, we will build on the Shot Put context from day 1. Continue the context storyline by recalling how last day, we used 4 red measuring sticks plus 12 feet to measure a throw of 76 feet and model this on the double number line: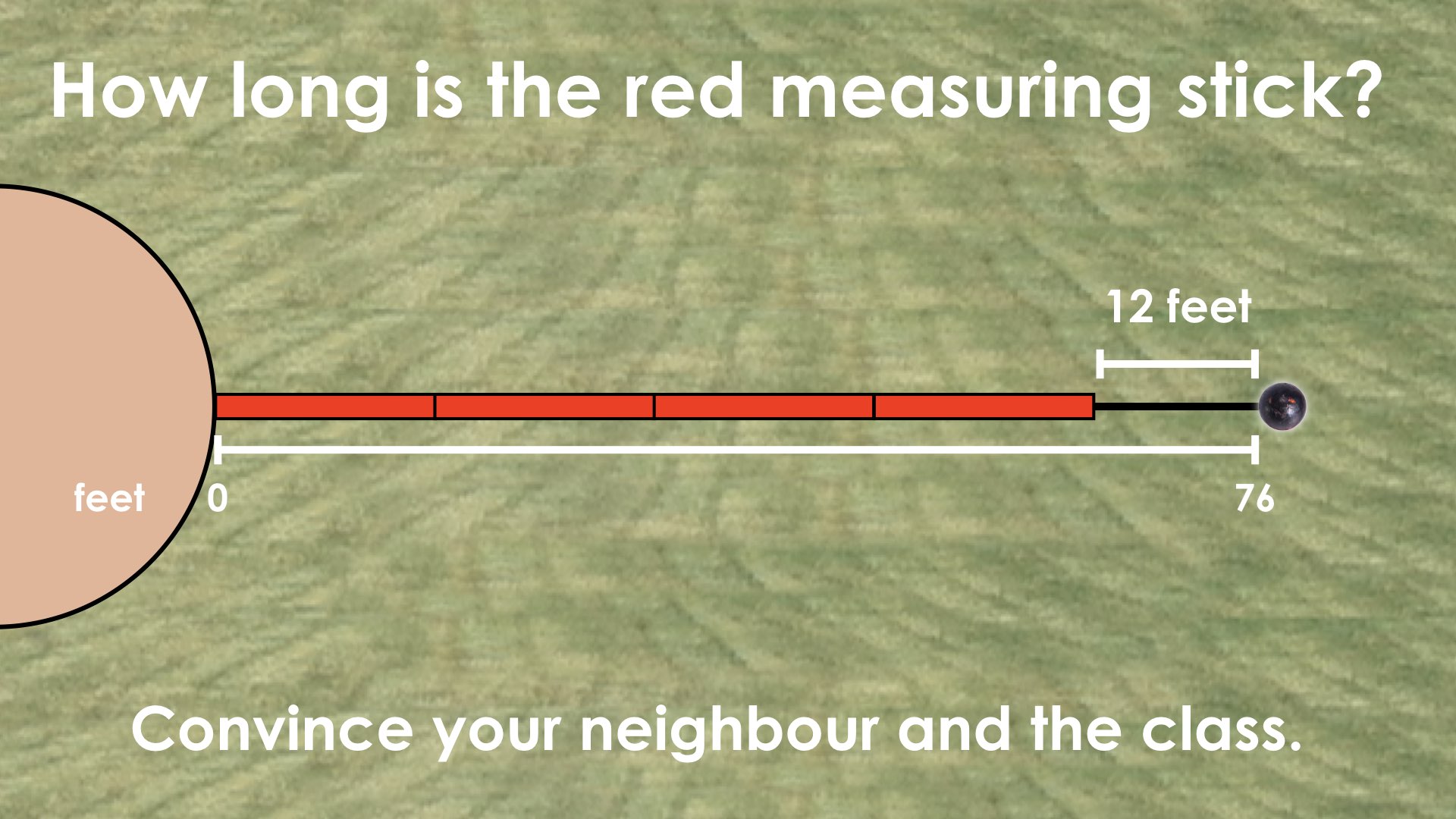 Problem #1:
Set-up the context for today’s math talk by stating:
Problem #1:
Set-up the context for today’s math talk by stating:
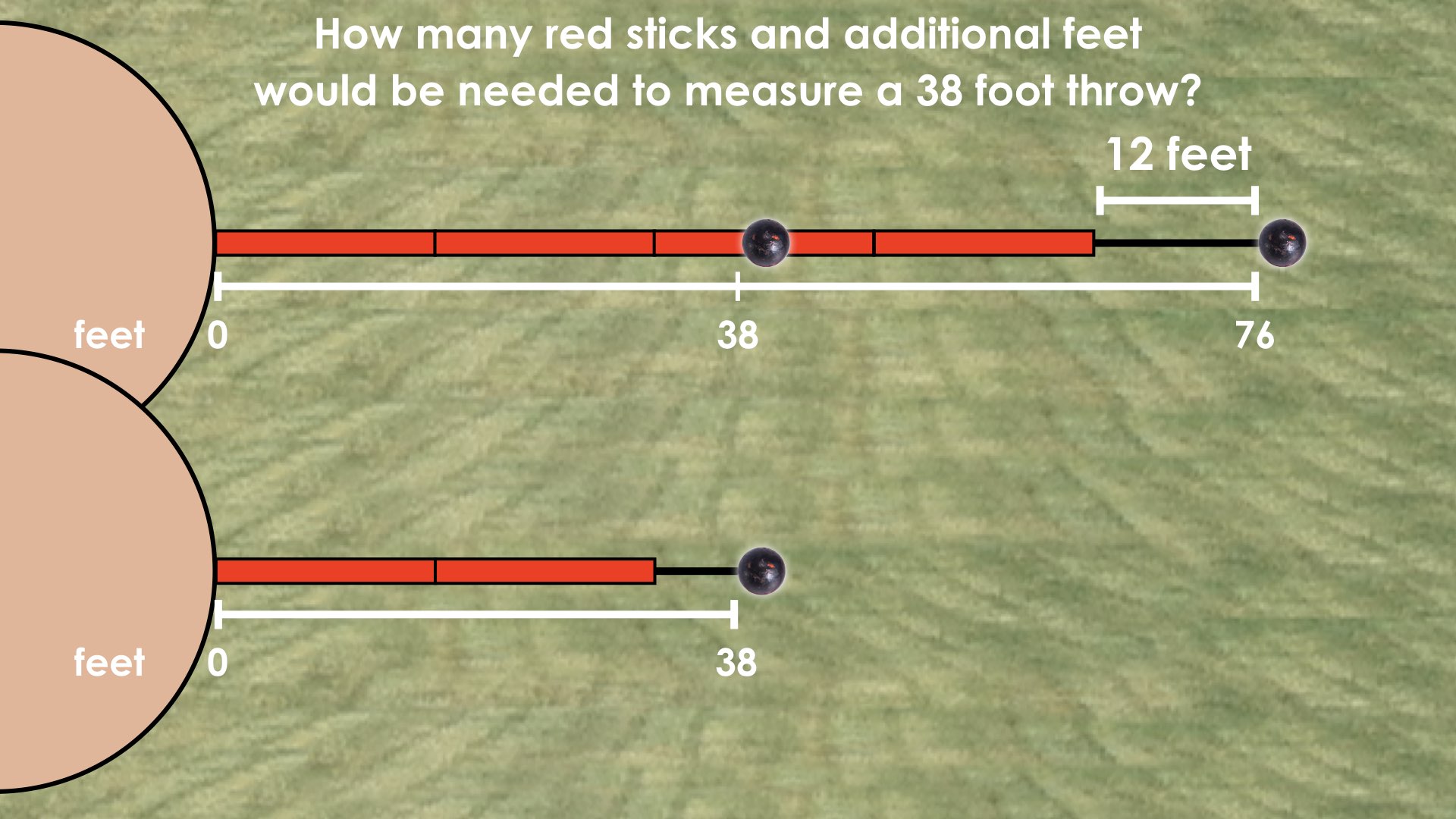
Today, a younger thrower had thrown a distance of 38 feet. How many red sticks and additional feet would be needed to measure the 38 foot throw?We recommend that you model the scenario by drawing the representation by hand of a number line and jumps to represent each measuring stick, plus the additional 12 feet. Some students may recall or calculate the length of the red measuring stick again with the learning from last day. Problem #2:
What about a 19 foot throw?
Facilitator Notes
For today’s Math Talk, we will build on the Shot Put context from day 1. Continue the context storyline by recalling how last day, we used 4 red measuring sticks plus 12 feet to measure a throw of 76 feet and model this on the double number line: Set-up the context for today’s math talk by stating:
Set-up the context for today’s math talk by stating:
Today, a younger thrower had thrown a distance of 38 feet. How many red sticks and additional feet would be needed to measure the 38 foot throw?
 We recommend that you model the scenario by drawing the representation by hand of a number line and jumps to represent each measuring stick, plus the additional 12 feet. Some students may recall or calculate the length of the red measuring stick again with the learning from last day.
We recommend that you model the scenario by drawing the representation by hand of a number line and jumps to represent each measuring stick, plus the additional 12 feet. Some students may recall or calculate the length of the red measuring stick again with the learning from last day.
 When we ask students where 38 feet should go on the number line, they should place it at the midpoint between 0 feet and 76 feet. For some students, they may need to decompose 76 into 70 + 6 to half both quantities separately as 35 + 3.
Alternatively, some students may choose to decompose 76 into 60 + 10 + 6 and half each quantity to get 30 + 5 + 3 to confirm that 38 is in fact the halfway point.
When we ask students where 38 feet should go on the number line, they should place it at the midpoint between 0 feet and 76 feet. For some students, they may need to decompose 76 into 70 + 6 to half both quantities separately as 35 + 3.
Alternatively, some students may choose to decompose 76 into 60 + 10 + 6 and half each quantity to get 30 + 5 + 3 to confirm that 38 is in fact the halfway point.
 From here, students will likely be able to see without too much trouble that you will need 2 red measuring sticks plus some number of additional feet.
The goal is that students will be able to realize that when we half the distance of 76 feet to 38 feet, we will need to half the number of red measuring sticks as well as the 12 additional feet.
From here, students will likely be able to see without too much trouble that you will need 2 red measuring sticks plus some number of additional feet.
The goal is that students will be able to realize that when we half the distance of 76 feet to 38 feet, we will need to half the number of red measuring sticks as well as the 12 additional feet.
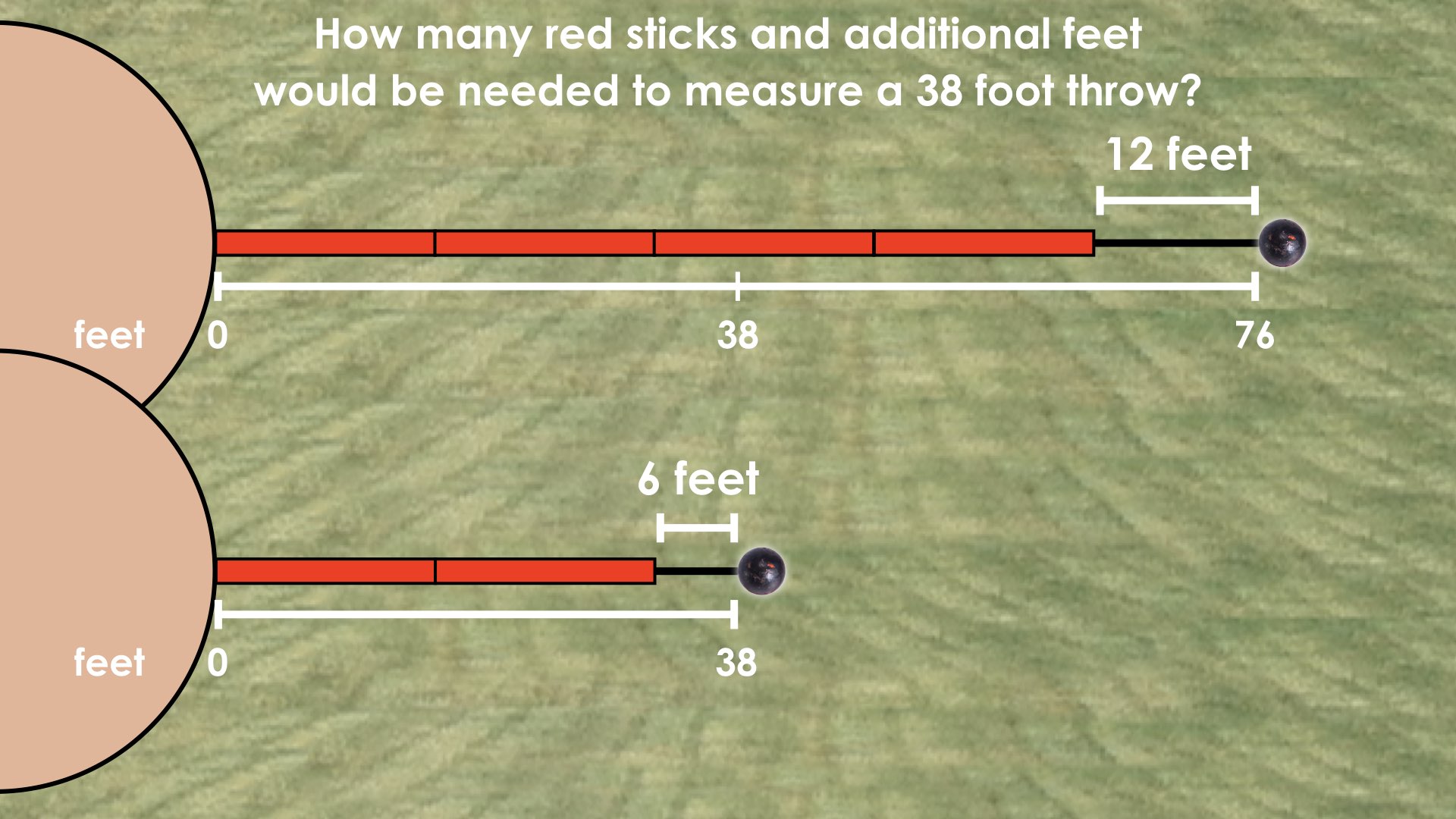
 By applying the idea of scaling both units, 76 feet and 4r + 12, by one half, our equation will remain equivalent.
By applying the idea of scaling both units, 76 feet and 4r + 12, by one half, our equation will remain equivalent.
 Now we can ask students the next question in the string of related problems:
Now we can ask students the next question in the string of related problems:
What about a 19 foot throw?
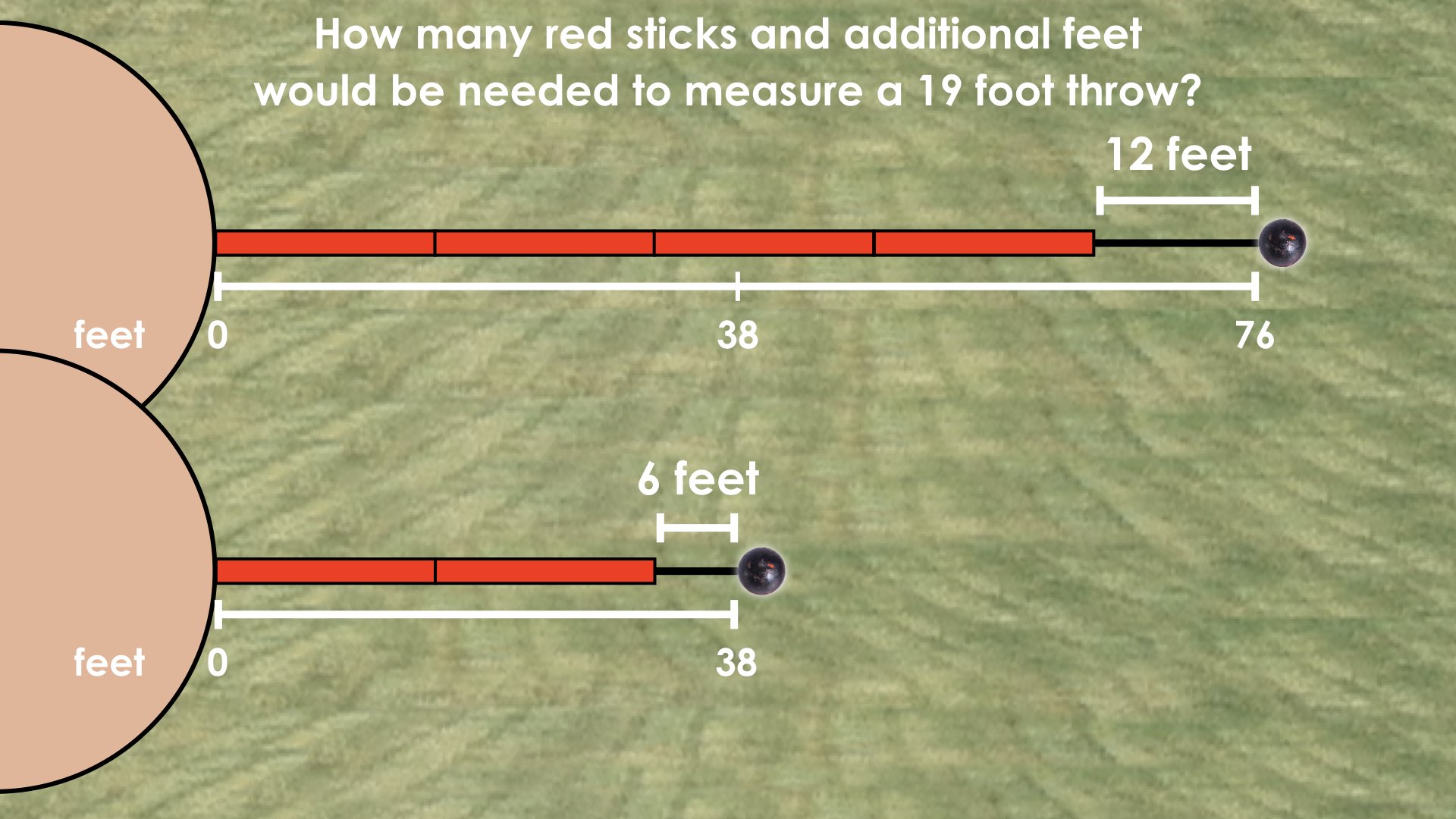 If we come to the conclusion that 19 feet is half of 38 feet, students may choose to use a similar strategy to how we modelled scaling in tandem in the last scenario.
If we come to the conclusion that 19 feet is half of 38 feet, students may choose to use a similar strategy to how we modelled scaling in tandem in the last scenario.
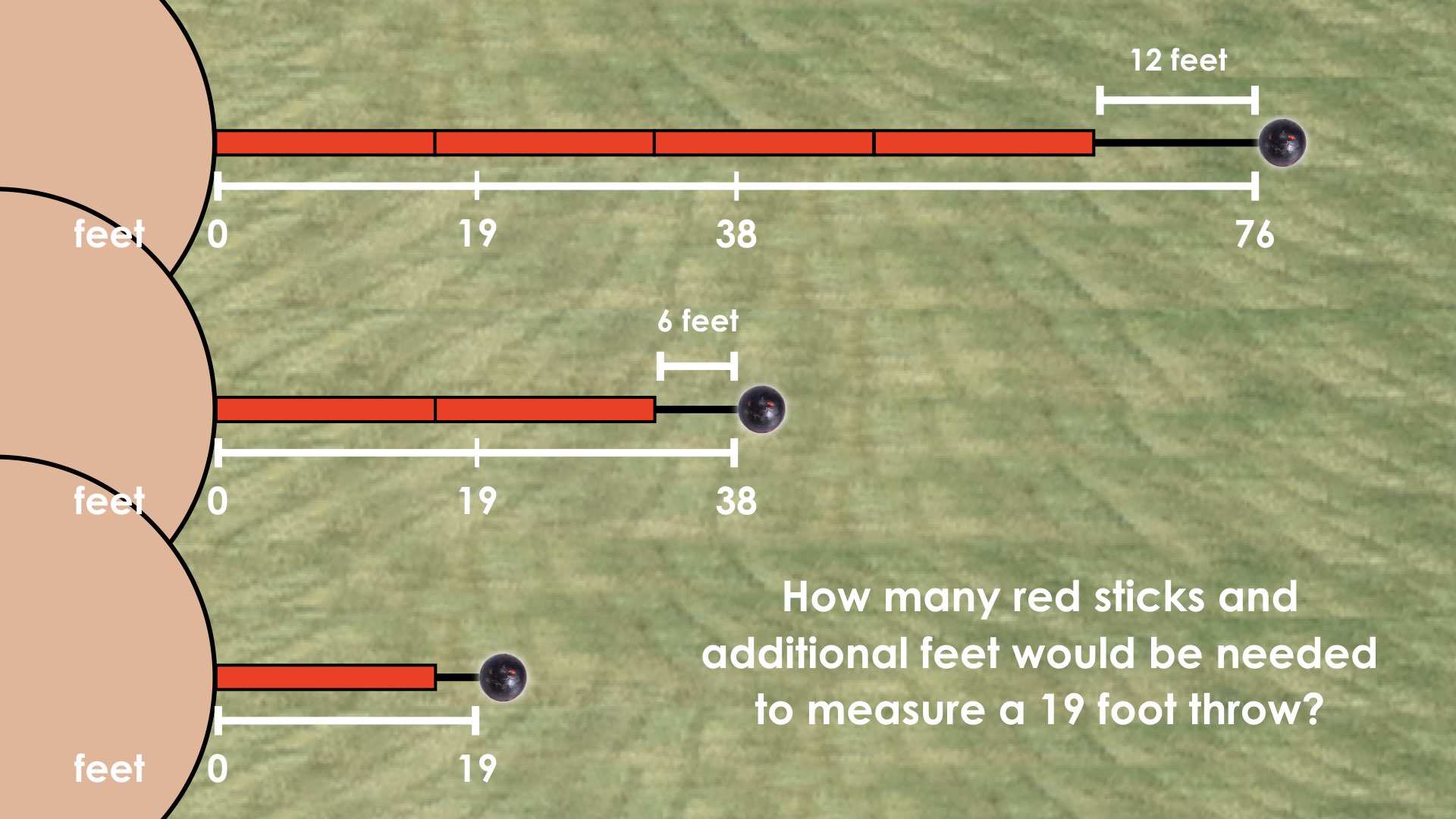 Consider using your double number line model from the first day to show how we can scale for these new throws.
If students are struggling to follow your hand drawn representation of the number line and feel showing a less abstract representation, you might consider sharing this silent solution animation and/or the following still frame images:
When students work on the 38 foot throw, take note of which students recognize that the total distance is half of the first throw, resulting in half the number of red sticks and half the number of additional feet required to measure. Be sure to highlight this strategy with the whole group.
This strategy reveals the big idea that both sides of an equation can be scaled as a single unit in tandem.
Note that the 19 foot throw is half of the 38 foot throw and a similar discussion can take place.
You might consider using the following visuals to assist in this math talk if none of the students are able to “see” or arrive at the fact that 38 feet is half of 76 feet, and half of 38 feet is 19 feet.
We would encourage the use of visuals only after you’ve attempted to ask students purposeful questions that will help them plot where each of those distances would go approximately on the number line.
Consider using your double number line model from the first day to show how we can scale for these new throws.
If students are struggling to follow your hand drawn representation of the number line and feel showing a less abstract representation, you might consider sharing this silent solution animation and/or the following still frame images:
When students work on the 38 foot throw, take note of which students recognize that the total distance is half of the first throw, resulting in half the number of red sticks and half the number of additional feet required to measure. Be sure to highlight this strategy with the whole group.
This strategy reveals the big idea that both sides of an equation can be scaled as a single unit in tandem.
Note that the 19 foot throw is half of the 38 foot throw and a similar discussion can take place.
You might consider using the following visuals to assist in this math talk if none of the students are able to “see” or arrive at the fact that 38 feet is half of 76 feet, and half of 38 feet is 19 feet.
We would encourage the use of visuals only after you’ve attempted to ask students purposeful questions that will help them plot where each of those distances would go approximately on the number line.
Big Idea
When students work on the 38 foot throw, take note of which students recognize that the total distance is half of the first throw, resulting in half the number of red sticks and half the number of additional feet required to measure. Be sure to highlight this strategy with the whole group. This strategy reveals the big idea that both sides of an equation can be scaled as a single unit in tandem. Note that the 19 foot throw is half of the 38 foot throw and a similar discussion can take place. You might consider using the following visuals to assist in this math talk if none of the students are able to “see” or arrive at the fact that 38 feet is half of 76 feet, and half of 38 feet is 19 feet. I would encourage the use of visuals only after you’ve attempted to ask students purposeful questions that will help them plot where each of those distances would go approximately on the number line.Spark Curiosity
Estimate: Revisiting The Context From Day 1
In order to revisit and begin building on the context from last day, we are going to share the following animation and/or screenshot image to allow students to make an estimate: Since it is unlikely that students will have a large range of values, you might consider skipping the too high and too low range strategy we tend to use when estimating. Having students make their best estimate and sharing with neighbours and the class is likely enough in this case.
The reveal is in the next section as it will lead us into the Fuel Sense Making portion of the lesson and first prompt for students to grapple with.
Since it is unlikely that students will have a large range of values, you might consider skipping the too high and too low range strategy we tend to use when estimating. Having students make their best estimate and sharing with neighbours and the class is likely enough in this case.
The reveal is in the next section as it will lead us into the Fuel Sense Making portion of the lesson and first prompt for students to grapple with. Fuel Sense-making
Walk Through Video
If you’d like to be walked through this math talk to gain a better understanding of the intentionality behind it, watch the following video:
Estimation Reveal & Productive Struggle Prompts
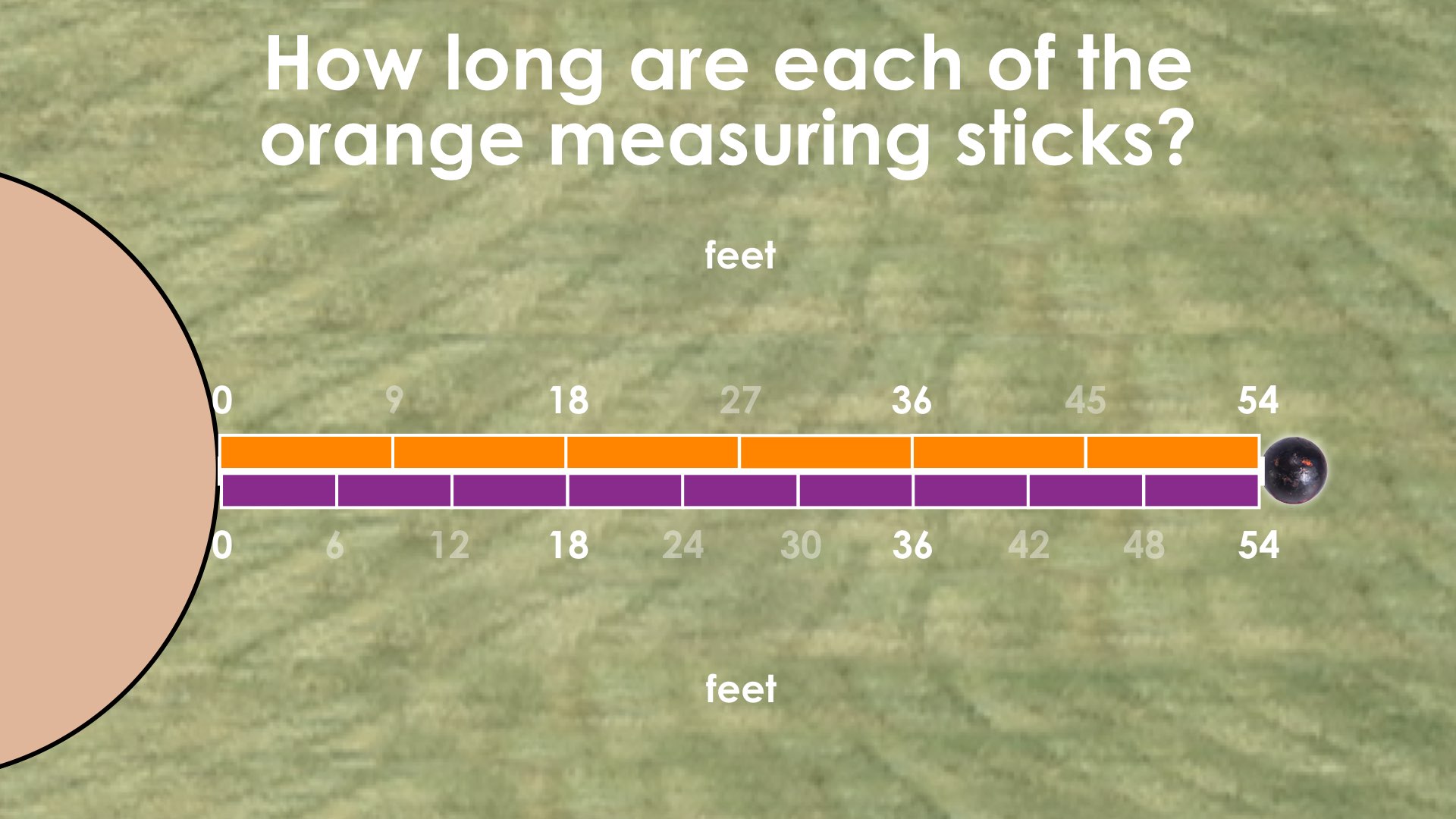
Share the following silent animation or screenshot image to reveal that this shot put throw could be measured with exactly 6 orange measuring sticks.
At the end of the animation, students will be prompted to determine the length of each orange measuring stick if the total distance of the shot put throw was 54 feet.
At this point, you can pose the following prompt for students:
Next up in the Shot Put competition, officials measured a throw to be 54 feet using 6 orange sticks exactly. How long are each of the sticks?
You may consider sharing the Prompt #1: Image as well:
You may choose to wait until students have determined the length of an orange measuring stick before sharing Prompt #2:
The opponent challenged the officials to measure with a purple stick that is 6 feet long. If the purple sticks were used to measure out the throw exactly, how many sticks must they have used?
Again, you may choose to wait to share Prompt #3 or share it at the same time as the previous prompt:
Conveniently, both the purple and orange sticks measured the 54 foot throw exactly.
Are there any other shot put throw lengths where this would occur? Use a model to convince us.
Facilitator Notes
In prompt 1 and 2, notice the relationship between 6 x 9 and 9 x 6 that is revealed through the context. In prompt #1, students are working with 6 groups (or sticks) of 9 feet, whereas in prompt #2, students are working with 9 groups (or sticks) of 6 feet. These two prompts require students to solve using division, but notice that prompt #1 uses partitive division, while prompt #2 uses quotative division. It should be noted that often times students can solve these prompts, but do not recognize that the type of division they use are flipped.
The purpose of prompt #3 is to emerge the equivalence between the number of purple sticks and the number of orange sticks. For example, when measuring 54 feet, students can see that 9 purple sticks is the same as 6 orange sticks. Through this prompt we are encouraging students to emerge the 2:3 ratio between the length of the orange and the length of the purple. This idea of equivalent expressions will be a fundamental big idea for subsequent lessons in this task based unit.
During Moves
While Students Are Productively Struggling…
Login/Join to access the entire Teacher Guide, downloadable slide decks and printable handouts for this lesson and all problem based units.
Student Approaches
Student Approach #1: Pictorial Set Model
Login/Join to access the entire Teacher Guide, downloadable slide decks and printable handouts for this lesson and all problem based units.
Student Approach #2: Number Line and Skip Counting
Login/Join to access the entire Teacher Guide, downloadable slide decks and printable handouts for this lesson and all problem based units.
Student Approach #3: Equations
Login/Join to access the entire Teacher Guide, downloadable slide decks and printable handouts for this lesson and all problem based units.
Next Moves
Reveal
After consolidating learning using student generated solution strategies and by extending their thinking intentionally, we can share what really happened by showing the following video/image revealing the possibilities for Prompts #1, #2, and #3.
Prompt #1 Answer: 9 feet per orange measuring stick.
Prompt #2 Answer: 9 purple measuring sticks.
Prompt #3 Answer: 18 feet, 36 feet, 54 feet, 72 feet, …
(all common multiples of 6 and 9)
Revisit the student answers.
Consolidation
Login/Join to access the entire Teacher Guide, downloadable slide decks and printable handouts for this lesson and all problem based units.
Reflect and Consolidation Prompts
Provide students an opportunity to reflect on their learning by offering this consolidation prompt to be completed independently.
Consolidation Prompt #1:
Login/Join to access the entire Teacher Guide, downloadable slide decks and printable handouts for this lesson and all problem based units.
Consolidation Prompt #2:
Login/Join to access the entire Teacher Guide, downloadable slide decks and printable handouts for this lesson and all problem based units.
Resources & Downloads
Login/Join to access the entire Teacher Guide, downloadable slide decks and printable handouts for this lesson and all problem based units.
Printable Lesson Plan PDF
Videos, Images & Media Files
Apple Keynote Presentation
Powerpoint Presentation
Printable Consolidation Prompts
Educator Discussion Area
Login/Join to access the entire Teacher Guide, downloadable slide decks and printable handouts for this lesson and all problem based units.
Explore Our 60+ Problem Based Units
This Make Math Moments Lesson was designed to spark curiosity for a multi-day unit of study with built in purposeful practice, number talks and extensions to elicit and emerge strategies and mathematical models.
Dig into our other units of study and view by concept continuum, grade or topic!