RICE RATIOS
RATIOS AND RATES
Use partitive division to reveal a rate and quotative division to determine a scale factor with both types of ratios.
Intentionality
Spark Curiosity
Fuel Sensemaking
During Moves
Student Approaches
Next Moves
Consolidation
Reflect and Consolidation Prompts
Resources & Downloads
Educator Discussion Area
Intentionality & Unit Overview

Length of Unit: 5 Days
Access each lesson from this unit using the navigation links below
Students will solve a problem about rice involving proportions. In solving the problem, they will consider ratio, rate, and scale.
Intentionality…
The purpose of this task is to give students an opportunity to apply their understanding of ratios and rates. Students will either scale the composed unit in tandem by revealing a scale factor, or leverage the rate that exists within this composed unit. Students will build fluency finding unknown values using ratio and/or rate reasoning. Students may or may not realize the role of division in revealing a rate or a scale factor. These are big ideas that will be explored more explicitly throughout this unit.
Some of the big ideas that may emerge in this task include:
- There are two types of ratios; composed unit and multiplicative comparison;
- A composed unit is often (not always) a ratio with two distinct units;
- A composed unit can be scaled in tandem;
- Equivalent ratios are derived from the same rate;
- When you divide a composed unit through partitive division, you reveal a rate.
- Quotative division is applied when trying to determine a scale factor between two quantities/measures of the same unit (i.e. rice and rice, water and water).
Prerequisite unit:
If your students do not currently have a solid understanding of the implications of division on ratio and rate reasoning, consider trying Planting Flowers before moving on to this unit.
Spark Curiosity
What Do You Notice? What Do You Wonder?
Show students the following video:
Ask students to engage in a notice and wonder protocol. ANYTHING and EVERYTHING that comes to mind is fair game.
Here’s some of the “everything and anything” students noticed and wondered on chart paper:
- I notice it is sunny outside.
- I notice a bag of rice.
- I wonder if they are going to cook rice?
- I wonder if there is enough rice for the whole family?
- I wonder how much rice is in the bag?
- I notice 200 mL of rice.
- I wonder how many servings he plans to make?
- I wonder how much water he will need to make 200 mL of rice?
- And many others…
At this point, take their noticing and wonders and try to answer any of the wonders you can cross off the list right away. Things like whether it was close to dinner time or whether the person was going to use the remainder of the package to make the rice are all things you want to answer, if you can.
Estimation: Prompt
Ask students to make an estimate based on what they saw in the previous video:
How much water will be needed to make 200 mL of rice?
Make an estimate.
Have students make estimates first by thinking about a measure of water that they believe will be too low, followed by a measure that they think will be too high.
Challenge students to be risky with their low/high estimates.
Then, have them pick their best estimate and share with their neighbours before sharing and recording on the chalk/whiteboard or chart paper as a class.
Ask students what information they might need in order to figure out the answer.
Fuel Sense-making
Crafting A Productive Struggle: Prompt
Show students the following video and follow-up with the prompt verbally:
After students have shared their estimates, re-iterate the estimation prompt, ask them to update their estimates and to craft a convincing argument for why they believe that quantity of water is necessary to make this batch of rice according to instructions.
Your prompt might sound something like this:
How much water will be needed to make 200 mL of rice?
Be more precise while also crafting a convincing argument using strategies and tools that would be easy to understand.
We will have students engage in this task without the aide of a calculator and thus we will promote the use of mathematical models as tools for thinking and representing their thinking.
Encourage students to convince their peers.
During Moves
While Students Are Productively Struggling…
If students are using algorithms and procedures with symbolic notation, be sure that they are able to clearly communicate why their strategy works. If they are unable to, ask them to attempt modelling either concretely or visually/pictorially.
Monitor student thinking by circulating around the room and listening to the mathematical discourse. Select and sequence some of the student solution strategies and ask a student from the selected groups to share with the class from:
- most accessible to least accessible solution strategies and representations;
- most common/frequent to least common/frequent strategies and representations; or,
- choose another approach to selecting and sequencing student work.
Discuss their strategies and elicit student thinking during your consolidation to build off of their current prior knowledge and understanding rather than “fixing” or “funnelling” student thinking to a strategy and/or model that does not connect to their strategy and/or approach.
Student Approaches
Student Approach #1: Leveraging The Ratio Of Water to Rice
I noticed that the instructions tell you to use twice as much water as rice since you use 500 mL of water for every 250 mL of rice. So, I just doubled 200 mL to get the amount of water that I needed. You need 400 mL of water if you have 200 mL of uncooked rice.
Student Approach #2: Scaling Down And Then Up
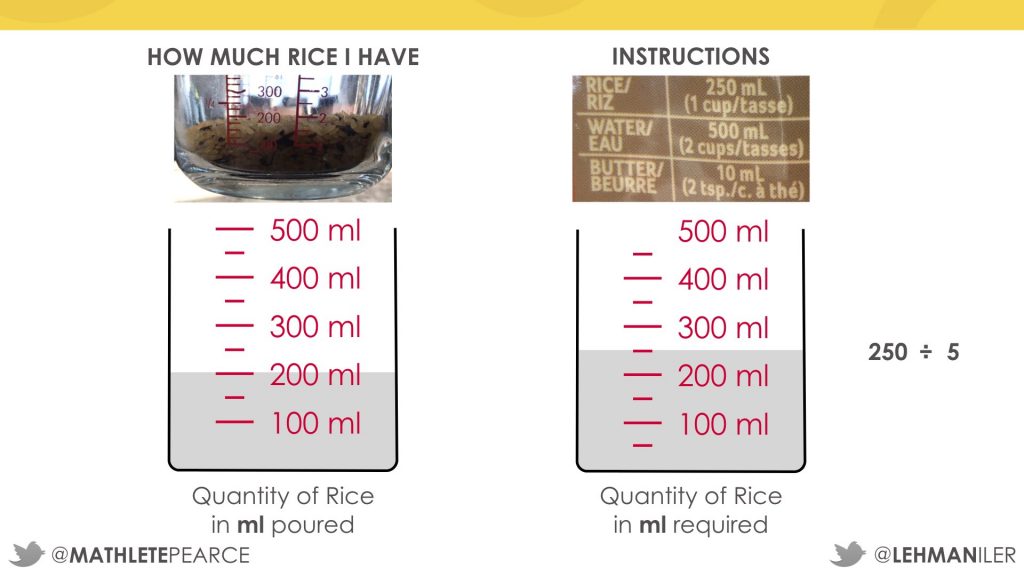
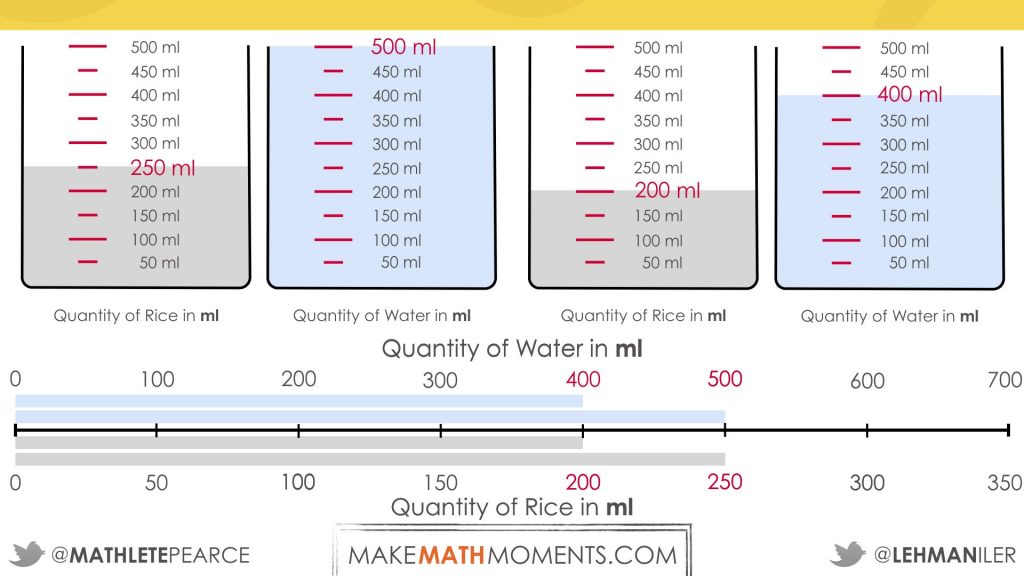
I drew a model showing measuring cups to compare the amount of rice in the question with the amount of rice in the instructions.
I need to figure out how to get from 250 (the amount of rice in the instructions) to 200 (the amount of rice in the question) using a scale factor. I know that both numbers are multiples of 50.
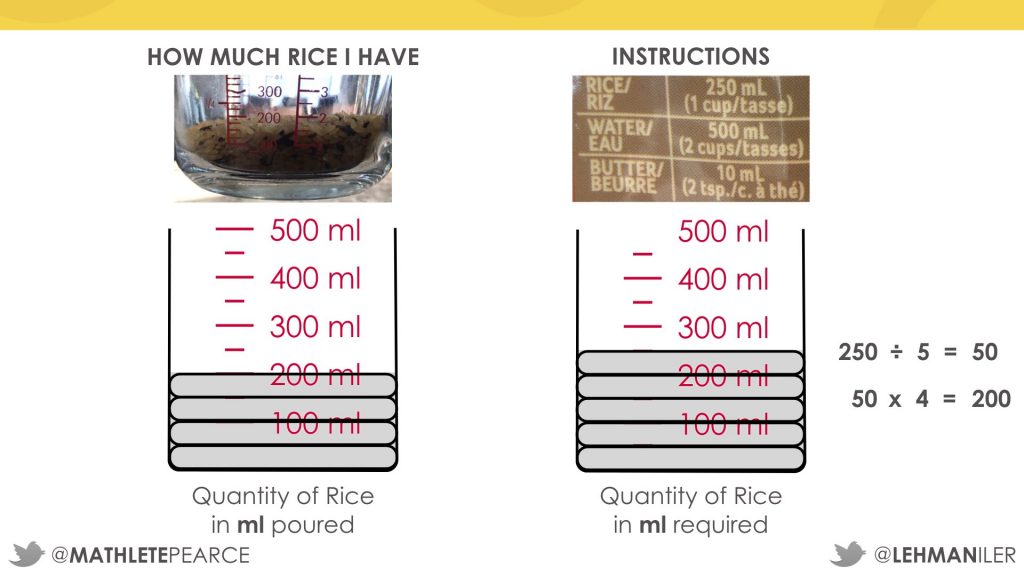
To get from 250 to 50, I divide 250 by 5.
Then to get from 50 to 200, you can multiply 50 by 4.
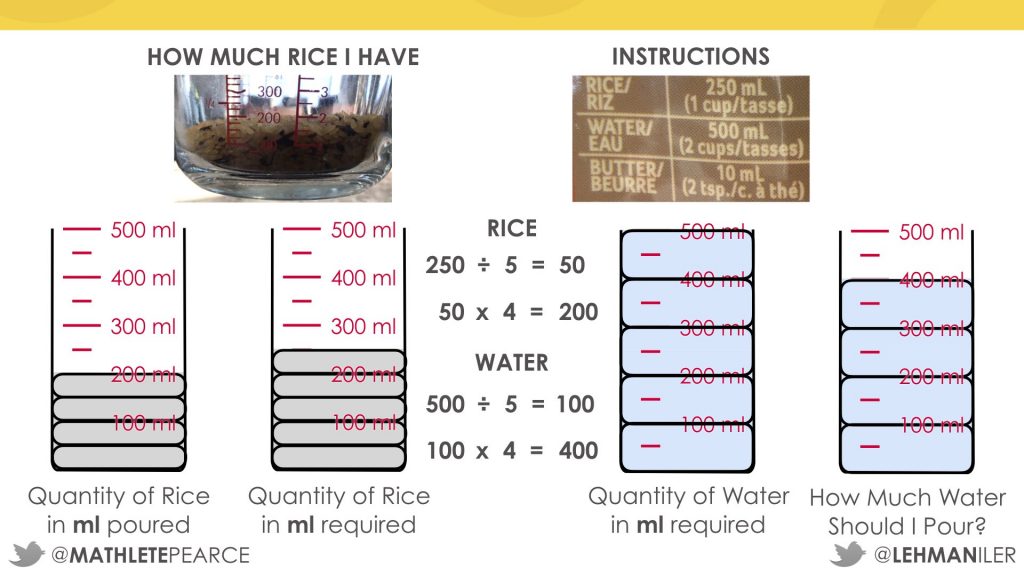
I can use the same scale factor to figure out how much water I need for 200 mL of rice: divide by 5, then multiply by 4.
I would need 400 mL of water.
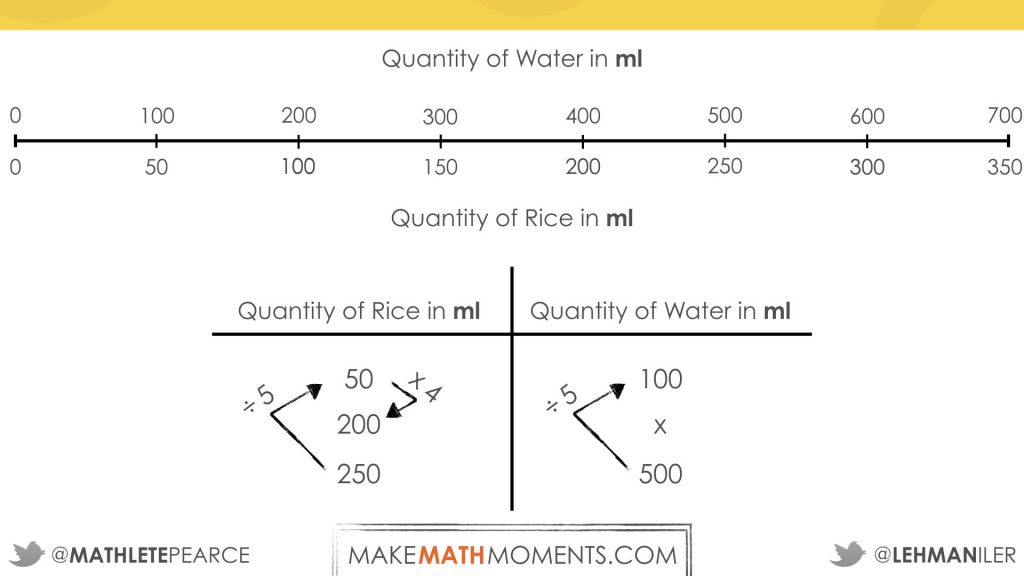
Student Approach #3: Scaling In Tandem With a Double Number Line
I used a double number line to compare the measure of uncooked rice with the measure of water needed to cook the rice.
The number line shows me the ratio of the measure of rice to the measure of water. I could tell from the number line that to make 200 mL of rice, I would need 400 mL of water.
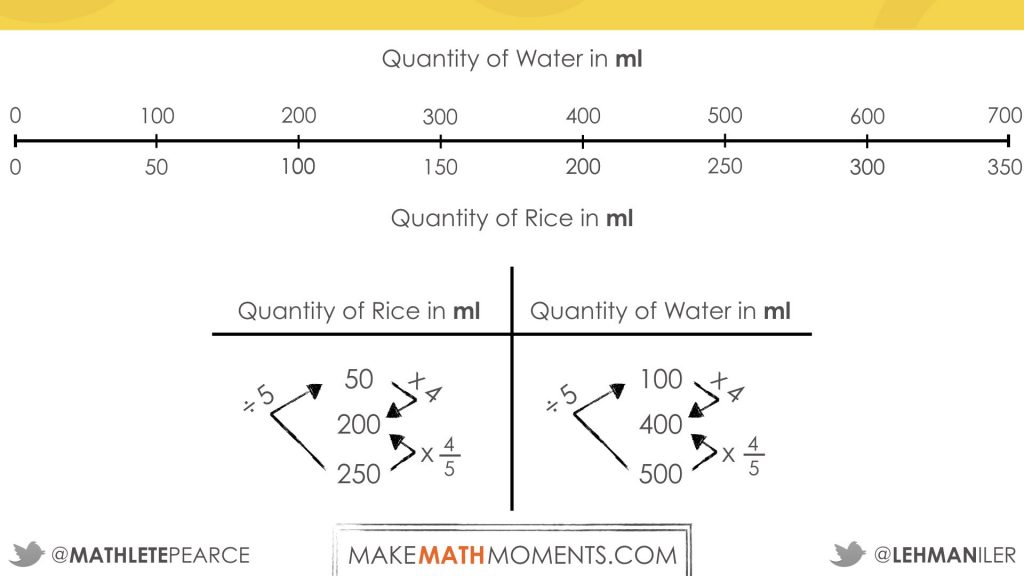
Student Approach #4: Scaling In Tandem By 4 Fifths
I can use a ratio table to scale both the measure of uncooked rice and water at the same time.
I know that 250 and 200 are both multiples of 50.
To get from 250 to 200, you can divide by 5 and then multiply by 4.
I can do the same thing with the water. First, I divide 500 by 5. Then, I multiply 100 by 4.
Discuss and consolidate the learning to ensure that the mathematical thinking you intended to elicit is clear to all students.
Consider explicitly drawing out the idea that “dividing by 5 and multiplying by 4″ is the same as “multiplying by 1 fifth and multiplying by 4″ or, in other words, multiplying by 4 fifths.
You might show this in a ratio table such as this one:
Student Approach #5: Multiplying By The Rate
I can use the constant of proportionality or rate reasoning to utilize the fact that for every 2 mL of water, I need 1 mL of rice.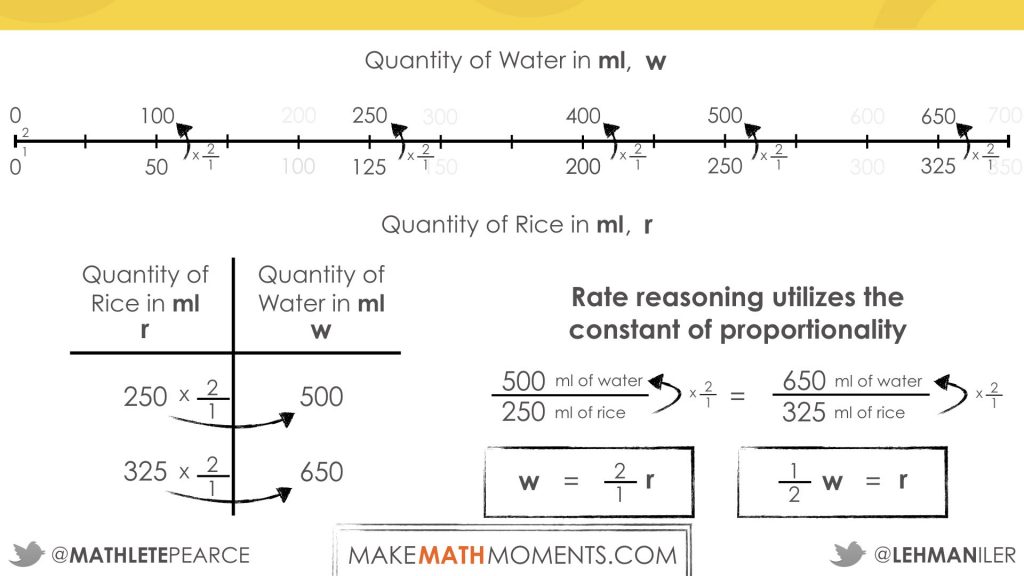
This means that I can use the rate of 2 mL of water per mL of rice to double any measure of rice to find the measure of water.
Inversely, I can use the inverse rate of 0.5 mL of rice per mL of water to half any measure of water to find the measure of rice.
Next Moves
Reveal
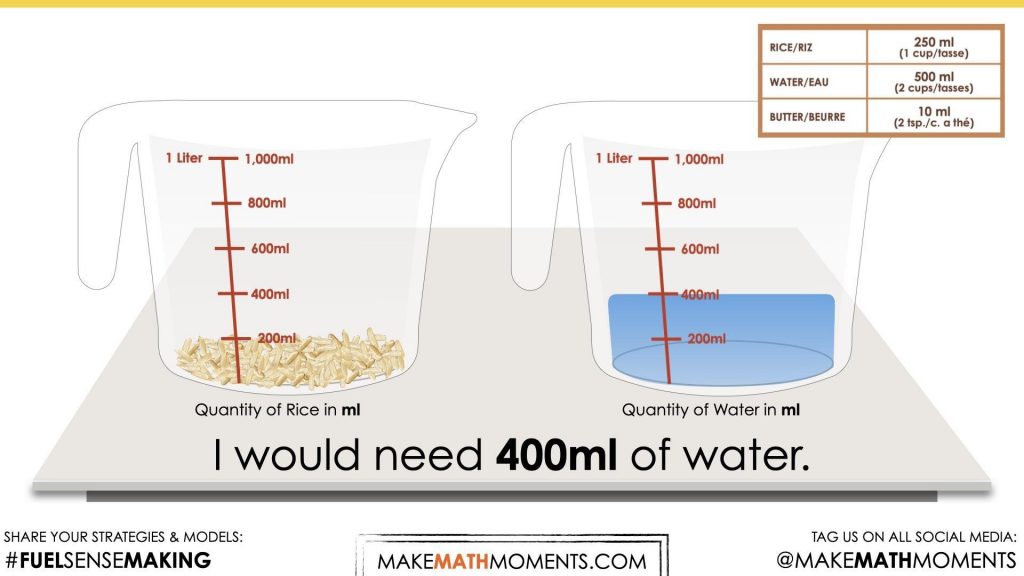
Once students have shared their answers, show them the video below.
And/or show the following screenshot:
Revisit the student answers. Have students discuss their thinking and what they would change if they did the task again. Return to the things students noticed and wondered from the SPARK section of the lesson, and answer any questions that have not been answered.
Consolidation
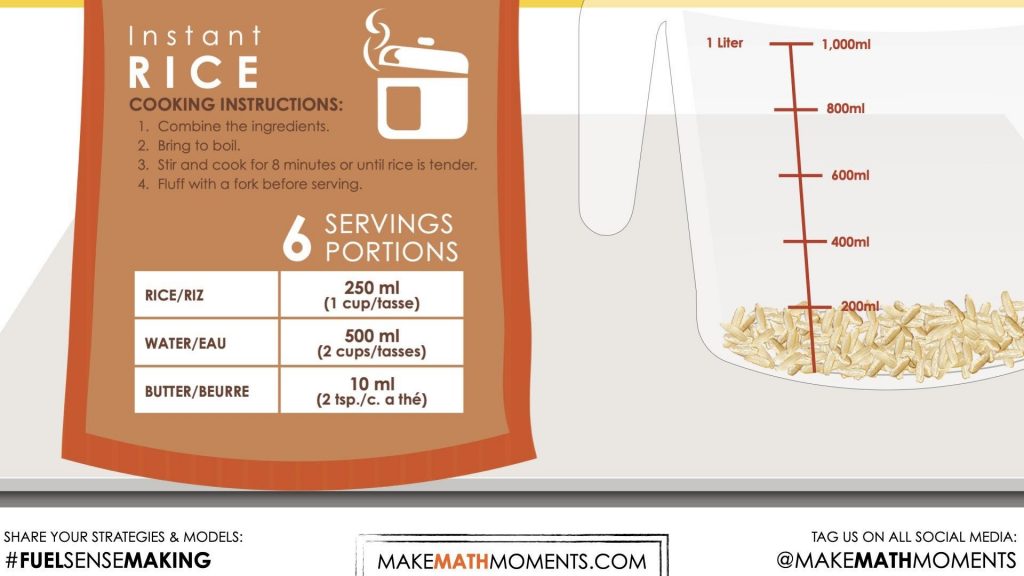
The comparison of the quantities of rice and water in this scenario is a specific type of ratio called a composed unit where one can consider the quantity in ratio as a single unit. For example, when we consider the 500 mL of water and 250 mL of rice required by the recipe, they can be considered as a single “unit” that increases and decreases together.
As we prepare to consolidate student thinking, you’ll notice that students likely approached this problem one of two ways: through rate reasoning by revealing a rate or ratio reasoning by scaling in tandem.
Select student solutions that leveraged both of these strategies (explained below) and use them to help facilitate a discussion comparing and contrasting the similarities and differences in each approach.
Rate Reasoning: Revealing a Rate
Students may have recognized the relationship between the water and the rice:
500 ml water : 250 ml rice
In this context, students may or may not have realized that they were leveraging a rate (2 ml of water : 1 ml of rice) through division. This rate that exists within a composed unit can be revealed through partitive division. 500 ml of water 250 ml of rice = 2 mL of water per mL of rice. The act of dividing may not have been necessary in this situation because the rate was obvious. However, as the relationships become less friendly, it might be worth noting the operator.
Ratio Reasoning: Scaling in Tandem
Students may have scaled the water and the rice by 4 fifths.
Student who approach the problem through this thinking will require both the rice and water to be scaled in tandem. If you have 4 fifths the measure of rice required by the recipe, then you also need 4 fifths as much water.
This scale factor can be revealed through quotative division:
200 ml of water 250 ml of water = ⅘
The use of quotative division in this case (dividing two quantities of the same unit) reveals a scale factor, or multiplicative comparison.
Reflect and Consolidation Prompts
Provide students an opportunity to reflect on their learning by offering these consolidation prompts to be completed independently.
Consolidation Prompt #1:
Select one of the approaches shared during today’s consolidation that differed from your own. Explain how it worked.
Use a model of your choice to communicate your understanding.
Consolidation Prompt #2:
How much butter would you need to add if you are cooking 200 mL of rice?
Use a model of your choice to justify your thinking.
Consolidation Prompt #3:
How much rice would you need if you plan on using 800 mL of water?
Use a model of your choice to justify your thinking.
Consolidation Prompt #4:
Liza wants to make a batch of lemonade. The recipe calls for 200 ml of water for every 250 g of sugar. Liza only has 200 g of sugar, how much water should she add?
Use a model of your choice to justify your thinking.
What You Could Do If…
…students have difficulty figuring out how much water they need when they’re using 200 mL of uncooked rice.
- You could … Encourage students to use groupable concrete materials such as linking cubes to represent and compare the amount of rice being used and the amount of rice in the instructions. For example, each linking cube can represent 50 mL. Help students see that if there are 5 linking cubes representing the rice in the instructions and 4 linking cubes representing the rice we’re using, the rice we’re using is actually 4 fifths of the rice in the instructions. So, they need 4 fifths of the amount of water in the instructions as well.
- You could … Promote students’ use of visual models such as an area model (as in Sample Response 2) or number lines drawn to scale (as in Sample Response 3) in order to leverage their spatial reasoning as they make visual comparisons.
Assessment For Learning
- Watch for students who see both types of ratios:
- the ratio of the measure of rice in the question to the measure of rice in the instructions (200:250).
- the ratio of rice to water (250:500).
- Watch for students who can articulate why the scale factor involves dividing by 5 and multiplying by 4. (E.g., The ratio 200:250 can also be written as 4:5, and this means we can use a factor of 4 fifths to figure out the amount of water.)
- Watch for students who use symbols and procedures without understanding to get to their answer. Ask these students to model their thinking concretely or visually so that they can better understand why the procedure they used actually works.
We suggest collecting this reflection as an additional opportunity to engage in the formative assessment process to inform next steps for individual students as well as how the whole class will proceed.
Resources & Downloads
Printable Lesson Plan PDF
Videos, Images & Media Files
Apple Keynote Presentation
Powerpoint Presentation
Printable Consolidation Prompts
Educator Discussion Area
Login/Join to access the entire Teacher Guide, downloadable slide decks and printable handouts for this lesson and all problem based units.
Explore Our 60+ Problem Based Units
This Make Math Moments Lesson was designed to spark curiosity for a multi-day unit of study with built in purposeful practice, number talks and extensions to elicit and emerge strategies and mathematical models.
Dig into our other units of study and view by concept continuum, grade or topic!