PROTEIN SHAKERS
FRACTION ADDITION
Explore addition of fractional quantities and regrouping through counting and unit fractions.
Intentionality
Spark Curiosity
Fuel Sensemaking
During Moves
Student Approaches
Next Moves
Extend #1
Extend #2
Resources & Downloads
Educator Discussion Area
Intentionality & Unit Overview

Current Length of Unit: 1 Day*
*This lesson is the first of an expected 5-day unit. The remaining four (4) days will be released as soon as they are available.
Students will:
- solve a problem involving the multiplication of a fraction by a whole number; and/or,
- solve a problem involving the multiplication of a fraction by a fraction.
The question(s) students will solve with this task are:
- How many scoops of mix do you need for 3 protein shakes?
- How many scoops of mix do you need for 1 and 1 half protein shakes?
This task is a great way to give students an opportunity to make connections between fractional thinking and proportional reasoning by determining how many fractional scoops of protein mix will be required to make a variety of protein shake servings.
This task provides an opportunity for students to approach a problem involving fractional thinking in different ways depending on their level of readiness: through counting, addition, or multiplication.
As is true for any task, the intentionality or learning objective can vary depending on what mathematical thinking you are hoping to elicit.
Spark Curiosity
What Do You Notice? What Do You Wonder?
Show students this video: Ask students to engage in a notice and wonder protocol. ANYTHING and EVERYTHING that comes to mind is fair game. Here’s some of the “everything and anything” students noticed and wondered on chart paper:- I notice a big container.
- I notice nice counters.
- I notice protein mix.
- I wonder if someone is going to make a smoothie?
- How much mix will be needed to make a smoothie?
- How much does that big container of protein mix cost?
- And many others…
Information: Video #2
Show this video and ask students if they have any more noticings and wonderings: After watching this clip, students had more noticings and wonderings:- I notice that less than a whole scoop of mix was used.
- I wonder if that was 3 fourths of a scoop?
- I wonder if they lost the “real” scoop and that’s why they can’t use a whole scoop?
- I how many scoops you’ll need for the 3 glasses?
- And many others…
Fuel Sense-making
Crafting A Productive Struggle: Prompt
Then, pose the following question:
I wonder how many scoops you’ll need for those 3 glasses?
Follow up that question with:
How might we convince someone that the quantity you come up with is correct?
Let them loose to make some estimates based on what they saw – even though they don’t yet know EXACTLY how many scoops was used on the single glass.
Ask students to estimate a number of scoops that they think is too high and a number of scoops that they think is too low before making their “best estimate”. After sharing out their estimates, without the aide of a calculator, have students improve the precision of their estimates by using the following information and they must convince their mathematical community of peers as well as the teacher.
During Moves
While Students Are Productively Struggling…
Monitor student thinking by circulating around the room and listening to the mathematical discourse. Select and sequence some of the student solution strategies and ask a student from the selected groups to share with the class from:
- most accessible to least accessible solution strategies and representations;
- most common/frequent to least common/frequent strategies and representations; or,
- choose another approach to selecting and sequencing student work.
The tools and representations you might see students using to convince their peers and/or the teacher include:
- Connecting cubes, square tiles, and/or relational rods used to model fractional amounts concretely.
- Area models and/or number lines drawn to make counting, adding, and/or multiplying unit fractions easier.
- As well as others…
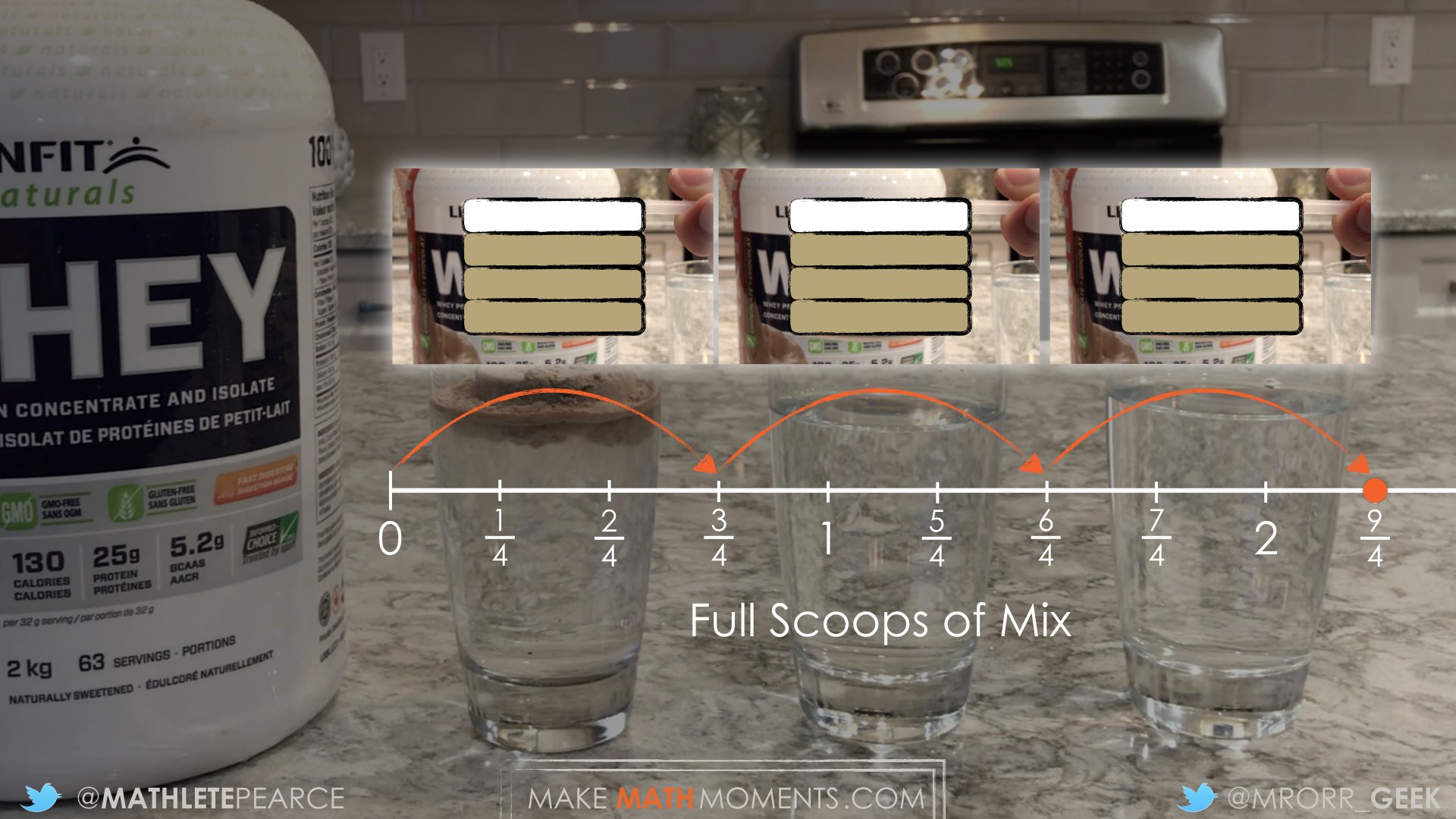
Have students share their strategies for determining the number of full scoops of powder needed to make three protein shakes. Ask them to convince you and their peers that their answer is correct by sharing mathematical models.
Discuss their strategies and elicit student thinking during your consolidation to build off of their current prior knowledge and understanding rather than “fixing” or “funnelling” student thinking to a strategy and/or model that does not connect to their strategy and/or approach.
Student Approaches
Student Approach #1:
I used an area model to represent 3 groups of 3 fourths.
I drew rectangles to represent the scoops.
So, I think that 9 fourths of a scoop of powder is needed to make three protein shakes.
9 fourths is the same as 2 full scoops and 1 fourth of a scoop.
Student Approach #2:
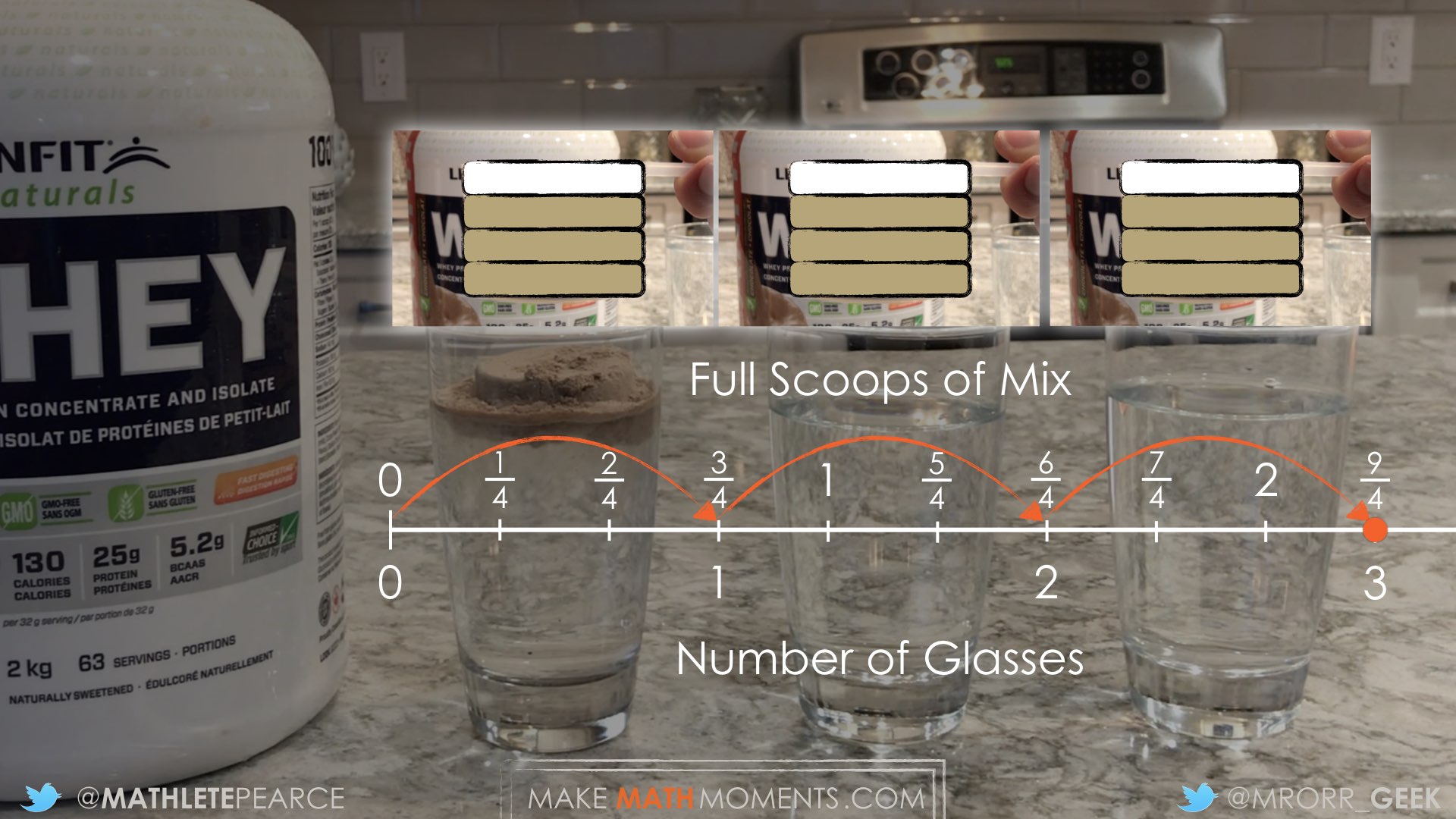
I used a number line to represent the 3 fourth jumps needed to make three glasses of protein shake.
I can think of it as a double number line.
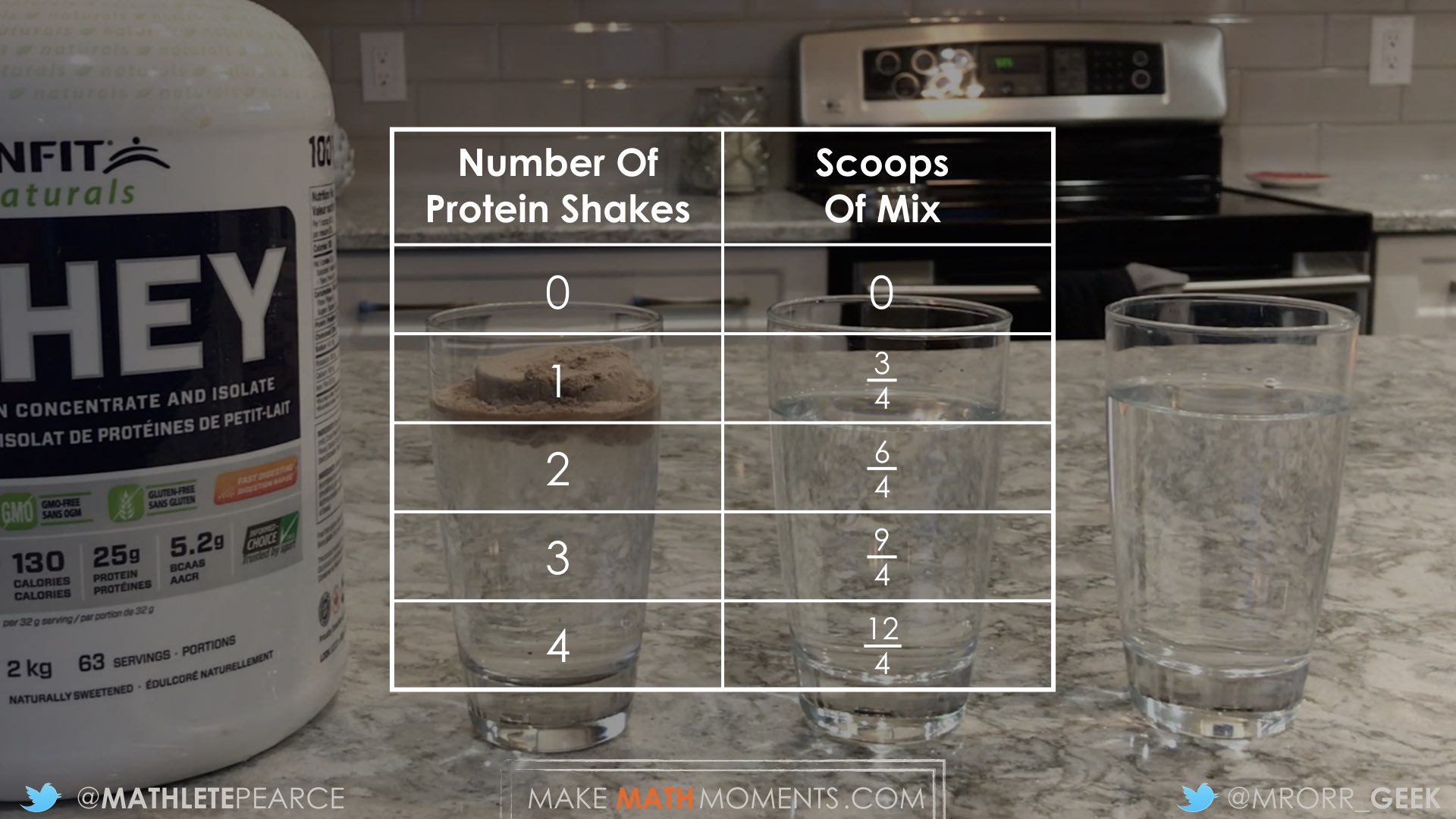
Or I could think of it as a ratio table.
So, I think that the quantity of mix needed to make three protein shakes is 9 fourth scoops. That is the same as 2 and 1 fourth scoops.
Student Approach #3:
I used repeated addition to multiply a whole number by a fraction.
3 fourths + 3 fourths + 3 fourths = 9 fourths of a scoop
9 fourths of a scoop is the same as 2 full scoops and 1 fourth of a scoop.
I could write this as:
3/4 + 3/4 + 3/4 = 9/4 scoops, or 2 1/4 scoops.
Or I could write it as:
3 x 3/4 = 9/4 scoops, or 2 1/4 scoops.
Discuss and consolidate the learning to ensure that the mathematical thinking you intended to elicit is clear to all students. For example, students may recognize that they can think of multiplication of a fraction by a whole number in terms of proportional reasoning.
Anticipate:
What do you think YOUR students might do with this task?
How might you modify this task to work in your classroom with your diverse learners?
If you want to be bold, test what you’ve anticipated by doing the task in your classroom and come back to report your thinking in the comments. As mentioned in many of our tasks, the learning goal you have selected for a task may be different than what I have in mind. This is especially true when we consider that this task could be used in a variety of classrooms with varying levels of student readiness.
Next Moves
Reveal #1: How Many Whole Scoops Were Used?
After consolidating learning using student generated solution strategies and by extending their thinking intentionally, we can share what really happened with this video.
Revisit the student answers. Have students discuss their thinking and what they would change if they did the task again.
Ask students why it makes sense that the three partial scoops turned into a little more than two full scoops.
Reveal #2: Re-unitizing From Improper Fraction to Mixed Numbers
In this video, students can watch as we re-unitize the protein mix powder from 9 fourth scoops (improper fraction) to 2 whole and 1 fourth scoops (mixed number).
Return to the questions you recorded earlier in the Notice and Wonder protocol during the SPARK section of the task and answer any questions that have not been answered.
Extend #1
Spark
Next, show students this video:
Students can share what they notice and wonder.
Estimation Prompt
We’ll land on this question:
How many scoops will be needed for 1 and 1 half protein shakes?
Students can see that we are still using 3 fourth scoops of protein mix per protein shake and can now use the necessary tools and representations to convince others of their solution.
Sense Making
While students are encouraged to use concrete and/or visual representations as tools for thinking as well as tools to represent their thinking, what I would like to explicitly highlight is that this question is asking:
How many 3 fourth scoops are in 1 and 1 half protein shakes?
Many students may still not recognize that the mathematical operation this question is eliciting is multiplication. Some students may choose to access this question through multiplication and repeated addition where students are solving the following:
1 1/2 protein shakes (groups of) 3/4 scoops per protein shake = ? scoops
In other words, we are evaluating:
1 1/2 x 3/4 = ?
or
3/2 x 3/4 = ?
I highly recommend using this task to introduce multiplication of fractions rather than as a “summary” or “review” as students can build models to construct their understanding of the multiplication of fractions.
We also do not want to simply rush to the procedure of multiplying “across” (i.e.: multiplying numerators and denominators) as this does not promote the fuelling of sense-making.
Student Response #1:
I used an area model to represent 1 and a half groups of 3 fourths, or 3 half groups of 3 fourths.
3/2 x 3/4
I drew rectangles, partitioned into fourths, to represent the scoops.
Since there is only half of the second 3 fourths of a scoop, I know that is the same as 3 eighths of a scoop. It makes sense to also partition the fourths from the whole scoop into eighths so the parts are the same size and easier to count.
We have a total of 9 eighths of a scoop, or 1 full scoop and 1 eighth of a scoop.
Student Response #2:
Using the same double number line that we used for finding the number of scoops to make 3 glasses of protein shakes, we can see that 1 and a half glasses wasn’t labelled on the double number line:
Since 1 and 1 half glasses is half way between our existing partitions, I can “half” each fourth of a scoop partition. This creates parts representing 1 eighth of a scoop (and 1 sixth of a glass).
There are 9 eighths of a scoop or 1 full scoop and 1 eighth of a scoop in 1 and a half protein shakes.
Students might also consider using a ratio table or their understanding of common denominators to find their solution.
Be sure to ask students to convince you of how they know their solution works. If they aren’t convinced themselves (i.e.: they ask you “am I right?” then you want to push them to represent their thinking another way to help them convince themselves and their peers vs. trusting an algorithm blindly.
Reveal: How Many Scoops Are In 1 and 1 Half Protein Shakes?
1 1/2 protein shakes (groups of) 3/4 scoops per protein shake = 9 eighth scoops
In other words:
1 1/2 x 3/4 = 9/8 scoops = 1 1/8 scoops
or
3/2 x 3/4 = 9/8 scoops = 1 1/8 scoops
Extend #2
Estimation Prompts
At this point, I would continue with this context by creating some additional problems that will allow students to “play” with addition, subtraction, and multiplication of fractions. You can even sneak in a few division of fractions problems to see how they handle them.
Some possible questions include:
How many scoops of protein shake mix will be required to make 8 protein shakes?
Don’t give students the operation, but for your own reference, the question above is asking:
8 protein shakes x 3 fourth scoops per protein shake = 24 fourth scoops = 24/4 scoops = 6 scoops
Another:
How many protein shakes were made if 12 1/2 scoops were used?
The question above is asking a quotative division problem that sounds like this:
12 1/2 scoops ÷ 3/4 scoops per protein shake = ? protein shakes
Which can be more easily solved by using the unit fraction of “fourths”. So let’s re-unitize our 12 1/2 scoops into fourths to get 50 fourths:
50 fourth scoops ÷ 3 fourth scoops = ? protein shakes
= 16 whole protein shakes and 2 fourth protein shakes
= 16 1/2 protein shakes
And finally:
How might your thinking have changed if only 1 fourth of the full scoop had been used each time? What if 2 thirds of a scoop had been used each time?
Next Moves
What Could You Do If…
…students have difficulty finding the number of full and partial scoops needed to make three protein shakes?
You could…
- …bring in a scoop similar in size and shape to the one used in the videos, with 1 fourth clearly marked and the other fourth lines shown. Fill it 3 fourths of the way. Ask students how full the scoop is and how they know. Ask if they think it will take 3 full scoops or more or less to make all three drinks.
- …ask students to use linking cubes to model the problem. Tell them that each linking cube represents 1 fourth of a scoop. Ask them to make a linking-cube train for each of the three glasses. Then ask students how many linking cubes they would need to represent a whole scoop. This prompt might help to push them toward regrouping based on the idea that 4 fourths make 1 whole scoop.
Assessment For Learning
Observe whether students explain how they arrived at their answer.
For example, can students do the following:
- use appropriate models to show their thinking
- explain their multiplicative thinking (e.g., “Since there are 3 fourths in each glass and there are 3 glasses, 3 groups of 3 fourths is 9 fourths.”)
- explain their strategy for arriving at a mixed number (e.g., “Since I need 3 fourths of a scoop for each of the 3 glasses, I know that I’m missing 1 fourth in each of the scoops. By taking 2 fourths and giving it to the first 2 scoops, I’ll get 2 full scoops with 1 fourth left over.”)
Resources & Downloads
Printable Lesson Plan PDF
Videos, Images & Media Files
Apple Keynote Presentation
Powerpoint Presentation
Educator Discussion Area
Login/Join to access the entire Teacher Guide, downloadable slide decks and printable handouts for this lesson and all problem based units.
Explore Our 60+ Problem Based Units
This Make Math Moments Lesson was designed to spark curiosity for a multi-day unit of study with built in purposeful practice, number talks and extensions to elicit and emerge strategies and mathematical models.
Dig into our other units of study and view by concept continuum, grade or topic!