PRISMS AND PYRAMIDS
VOLUME OF PRISMS AND PYRAMIDS
Students will explore the relationship between the volume of a prism and the volume of a pyramid by first estimating and then observing how many pyramids will fit in a prism with the same base and height.
Intentionality
Spark Curiosity
Fuel Sensemaking
During Moves
Student Approaches
Next Moves
Consolidation
Reflect and Consolidation Prompts
Resources & Downloads
Educator Discussion Area
Intentionality & Unit Overview

Current Length of Unit: 1 Day*
*This lesson is the first of an expected 5-day unit. The remaining four (4) days will be released as soon as they are available.
Through this problem based math lesson, students will determine how many pyramids will fit in a prism by either repeatedly filling and pouring water, sand, beads or another material from a physical pyramid and prism or by leveraging the included video clips as a means to first estimate and then observing the result of the investigation.
Some of the big ideas that may emerge from this problem based math lesson include:
- The volume of a 3-dimensional figure can be found by determining the number of cubic units that can be contained within the figure;
- The volume of a prism can be determined by finding the number of cubic units required to cover the base and multiply by the number of layers (i.e.: the height); and,
- The volume of a pyramid is one-third the volume of a prism with a congruent base and equivalent height. Therefore, the volume of a cone is also one-third the volume of a cylinder with a congruent base and equivalent height.
Spark Curiosity
What Do You Notice? What Do You Wonder?
Show students the following video:
Then, ask students:
What do you notice?
What do you wonder?

Give students 60 seconds (or more) to do a rapid write on a piece of paper.
Then, ask students to share with their neighbours for another 60 seconds.
Finally, allow students to share with the entire group.
Some of the noticing and wondering that may arise include:
- I notice two 3D figures.
- I notice a prism and a pyramid.
- They both have a square for their base.
- I wonder why we’re looking at shapes?
- I wonder what they’re going to do with those figures?
- How much wrapping paper would it take to wrap those figures?
- How many of the pyramid will it take to fill the prism?
- And many more.
At this point, you can acknowledge some of the details that students noticed and answer any of the wonders that will not reveal too much information as to take away from the intentionality of the lesson.
Estimation: Video & Prompt
Share the following video:
Prompt students with:
How many square base pyramids will it take to fill the square base prism?
Make an estimate.
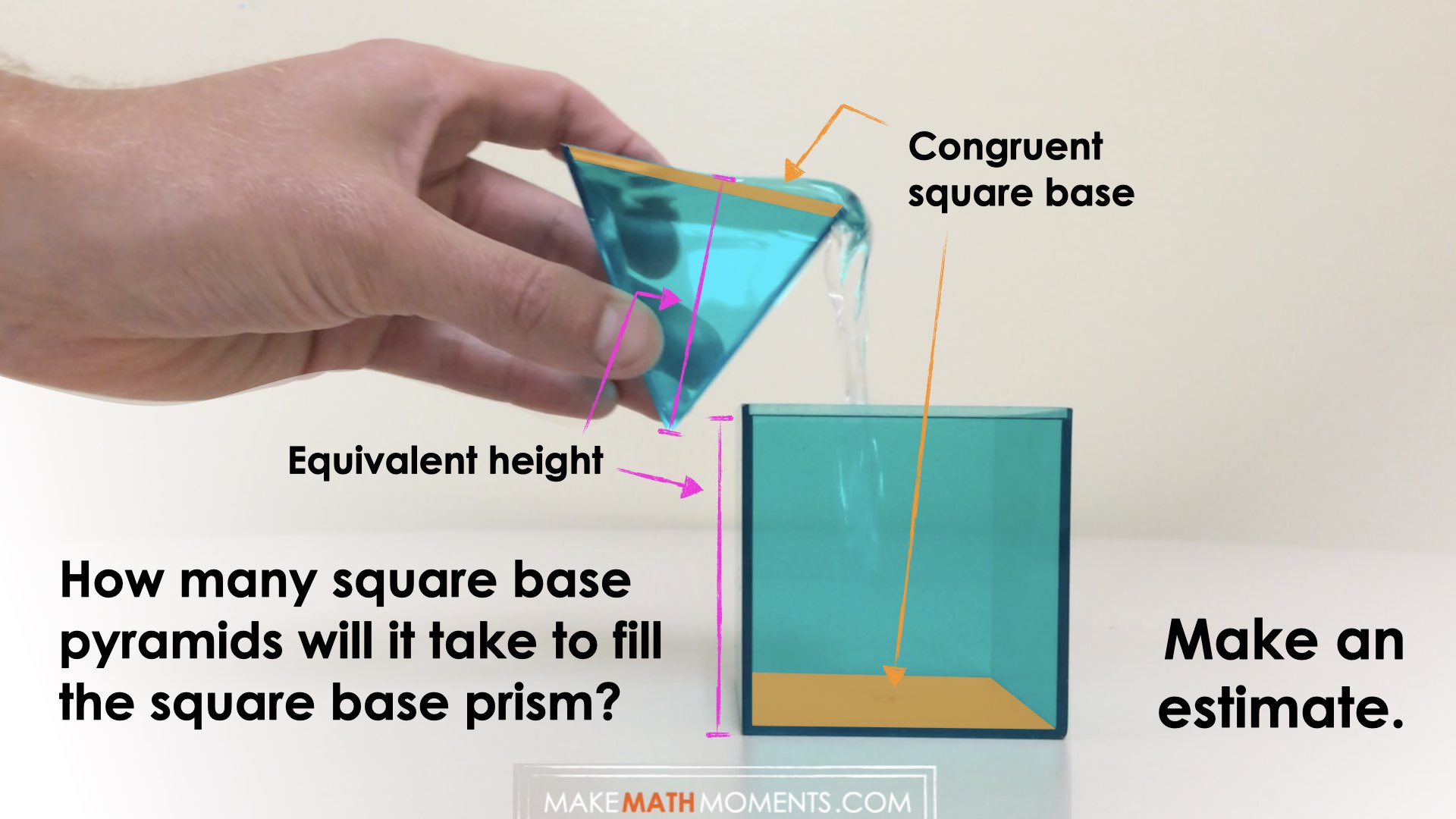
Be sure students are made aware that the prism and the pyramid both have a congruent square base (i.e.: the same base) and an equivalent height (i.e.: the same height).
We can now ask students to make an estimate using their spatial reasoning as to how many square base pyramids it will take to fill the square base prism. Encourage students to share their predictions and justification with neighbours before welcoming them to the group as a whole.
Update Estimate: Video & Prompt
Share the following video:
Prompt students with:
How many square base pyramids will it take to fill the square base prism?
Update your estimate.

Monitor student thinking by circulating around the room and listening to the mathematical discourse. Encourage students to use precise mathematical language where appropriate and listen for the use of additive thinking (it will take one more pyramid to fill the prism) or multiplicative thinking (the prism can hold 2 and ½ pyramids of water).
Allow students to share their estimates with neighbours first, then with the class. Write down their estimates on the chalkboard/whiteboard/chart paper so students feel their voices are being heard and so they feel they have a stake in solving this problem. At this point, encourage students to describe their thinking so that anyone could be convinced of their estimate.
Fuel Sense-making
Crafting A Productive Struggle: Prompt
Show students the productive struggle prompt video:
While the video is playing, you can narrate what students see to reveal the struggle prompt for this task:
Along with updating your estimate of how many square based pyramids will it take to fill the square based prism, also make an estimate of:
- how many triangular based pyramids it will take to fill the triangular based prism; and,
- how many cones will it take to fill the cylinder?
Note that each prism and pyramid we are comparing has a congruent base and equivalent height.

After you give students an opportunity to make an estimate and share with neighbours and to the group, prompt students to investigate the volume relationships between each pair of prisms and pyramids by filling and pouring water, sand, rice or similar into geometric solids from a math manipulative kit or by creating their own prisms and pyramids using the provided templates.

While it may be tempting for educators to skip over the opportunity for students to construct their own prisms and pyramids due to the time it will require, note that this is an opportunity for students to better spatially recognize each figure by exploring their nets and also to deeply investigate the volume relationships from each pyramid and prism with a congruent base and equivalent height.
During Moves
While Students Are Productively Struggling…
Monitor student thinking by circulating around the room and listening to the mathematical discourse. Select and sequence some of the student solution strategies and ask a student from the selected groups to share with the class from:
- most accessible to least accessible solution strategies and representations;
- most common/frequent to least common/frequent strategies and representations; or,
- choose another approach to selecting and sequencing student work.
Some students may be quick to conclude that the surface area of each pyramid is significantly less than the surface area of each congruent base and equivalent height prism, which may influence them to update their estimate as they construct each solid. Listen for students who are making multiplicative comparisons as they approximate the surface area of a pyramid to be “half” or maybe “one third” of the surface area of the respective prism.
What are students saying as they pour sand, rice, or other easy to pour materials from a prism into a pyramid? Are their estimates becoming more precise and closer together as a group?
Discuss their thinking during your consolidation to build off of their current prior knowledge and understanding rather than “fixing” or “funnelling” student thinking.
Student Approaches
Student Approach #1: Skip Counting
When I cut out the net of each figure, I noticed that the surface area of each pyramid was much smaller than the surface area of each prism. This made me think that maybe the volume of each pyramid would actually be less than my original estimate of 2 pyramids to fill a prism.
Student Approach #2: Pouring And Updating
After I constructed each prism and pyramid, I filled each pyramid with rice and poured it into the prism with the same base and height. I could fit about 3 pyramids in the prism for each pair of solids.
Student Approach #3: Generalizing a Formula For Volume of a Pyramid
After realizing that it took 3 pyramids to fill a prism, I realized that the formula for any pyramid could be found by simply taking the volume of the prism with the same base and height and multiplying by 1 third (or dividing by 3).
Next Moves
Reveal
Show students the following reveal video:
Consider leaving the final frame up for students to reflect on and discuss as you prepare to head into the consolidation of the lesson.

Consolidation
While all students are now keenly aware that it requires 3 pyramids to fill a prism with a congruent base and equivalent height, do not assume that all students will independently make the connection that they can then simply modify the formula for each congruent base prism and take 1 third of that quantity.
In order to ensure we explicitly bring this idea to the forefront, we can prompt students with:
What might the formula be to determine the volume of each pyramid?
Discuss with your neighbour.

Consider leveraging the silent solution video animation below or the supporting slides included in the downloads section to ensure students make the connection between the volume relationship of each prism and pyramid with their symbolic volume formula.
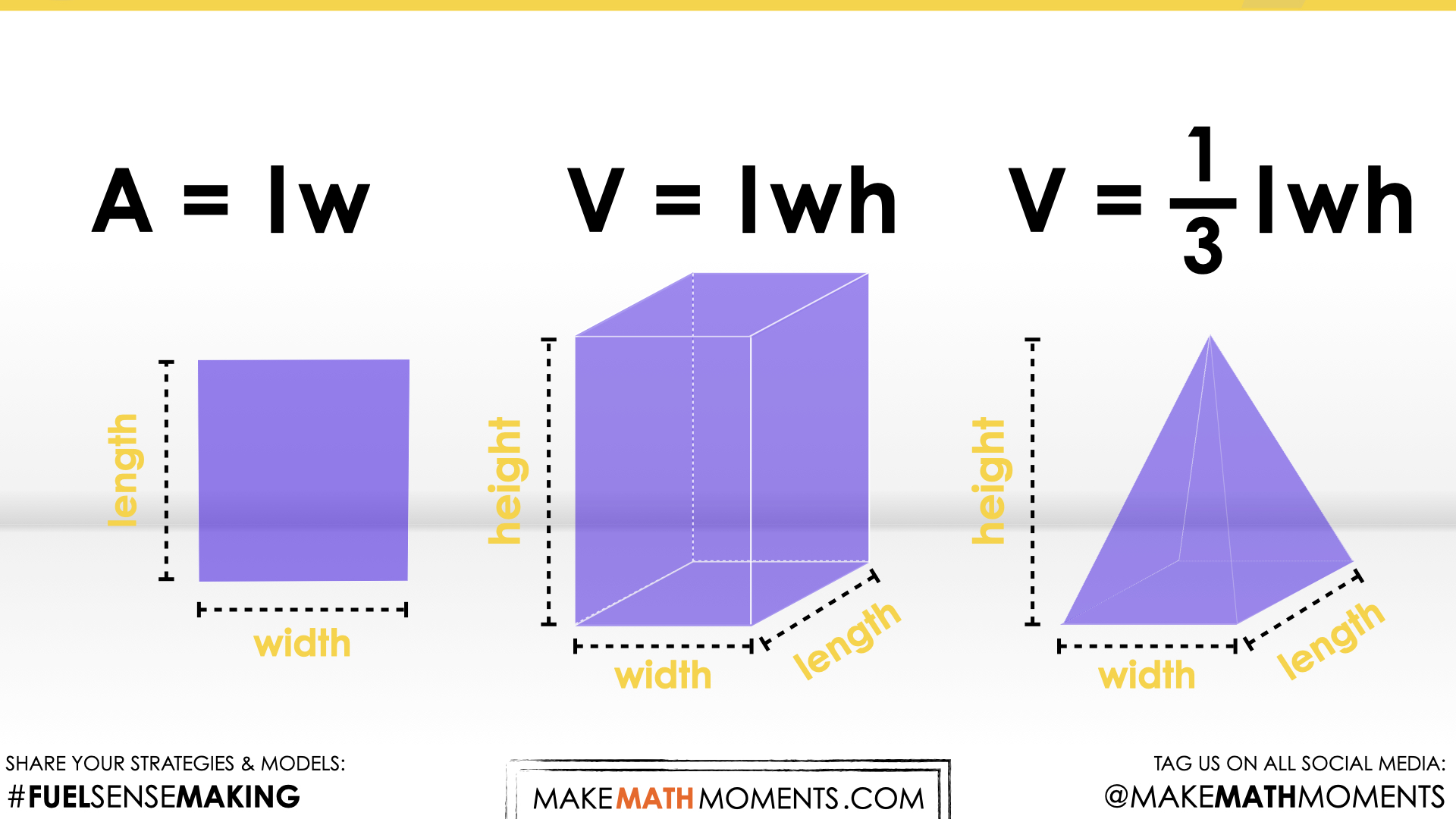
Deriving Formula for the Volume of a Square-Based Pyramid
In this silent solution animation video, we attempt reiterating what was discovered through investigation today. By determining the volume of a square (or rectangular) based prism by calculating the area of the base times the height, we can easily determine the volume of the same base and height pyramid by taking 1 third of that volume or dividing the volume by 3.
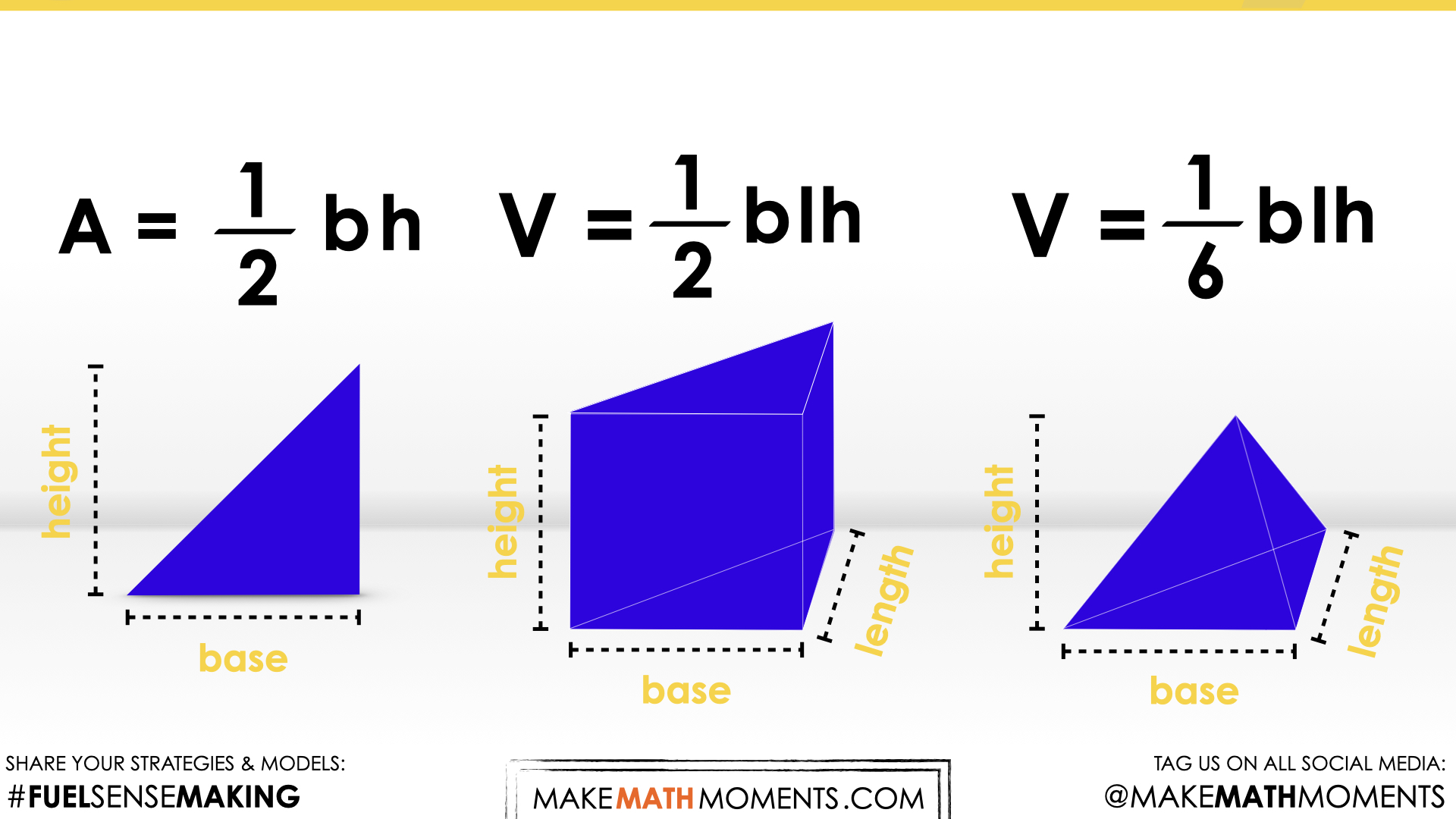
Deriving Formula for Volume of a Triangular Based Pyramid
The same is true for the relationship between any prism and pyramid as we can see with this silent solution video of a triangular based prism and pyramid.
While students may feel confident that they understand the 1 to 3 relationship between a pyramid and prism with the same base and height, exploring these silent solution animations can be helpful to reinforce our understanding of how we determine volume in general as well as how we can extend this thinking to pyramids.
Deriving Formula for the Volume of a Cone (Circular Based Pyramid)
And despite the naming convention being a little different for circular based prisms (cylinders) and pyramids (cones), the relationship still holds true.
These explorations are critical in helping students build a concrete foundation in understanding how the volume of 3-dimensional figures can be determined as well as how they relate to one another.

Reflect and Consolidation Prompts
Provide students an opportunity to reflect on their learning by offering these consolidation prompts to be completed independently.
Consolidation Prompt #1:
Why would it be useful to know both the formulas for the volumes of cubes and pyramids and the relationship between their volumes?
Consolidation Prompt #2:
A cylindrical storage container full of grain is going to be poured into a cone shaped storage container with a congruent circular base and an equivalent height.
What fraction of the whole cylindrical container will be…
- … full of grain?
- … empty?
Create a convincing argument explaining how you know.
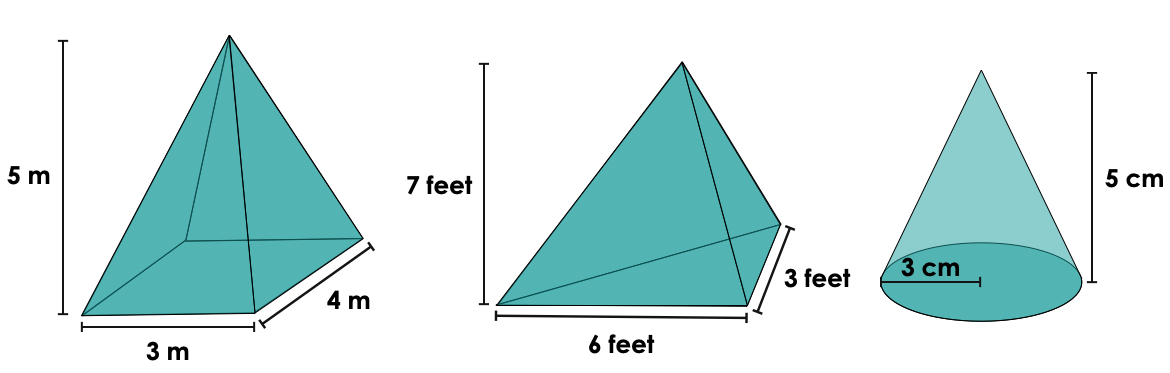
Consolidation Prompt #3:
Determine the volume of each pyramid.
Show how you know.
We suggest collecting this reflection as an additional opportunity to engage in the formative assessment process to inform next steps for individual students as well as how the whole class will proceed.
Resources & Downloads
Printable Lesson Plan PDF
Videos, Images & Media Files
Apple Keynote Presentation
Powerpoint Presentation
Printable Template
Printable Consolidation Prompts
Educator Discussion Area
Login/Join to access the entire Teacher Guide, downloadable slide decks and printable handouts for this lesson and all problem based units.
Explore Our 60+ Problem Based Units
This Make Math Moments Lesson was designed to spark curiosity for a multi-day unit of study with built in purposeful practice, number talks and extensions to elicit and emerge strategies and mathematical models.
Dig into our other units of study and view by concept continuum, grade or topic!



