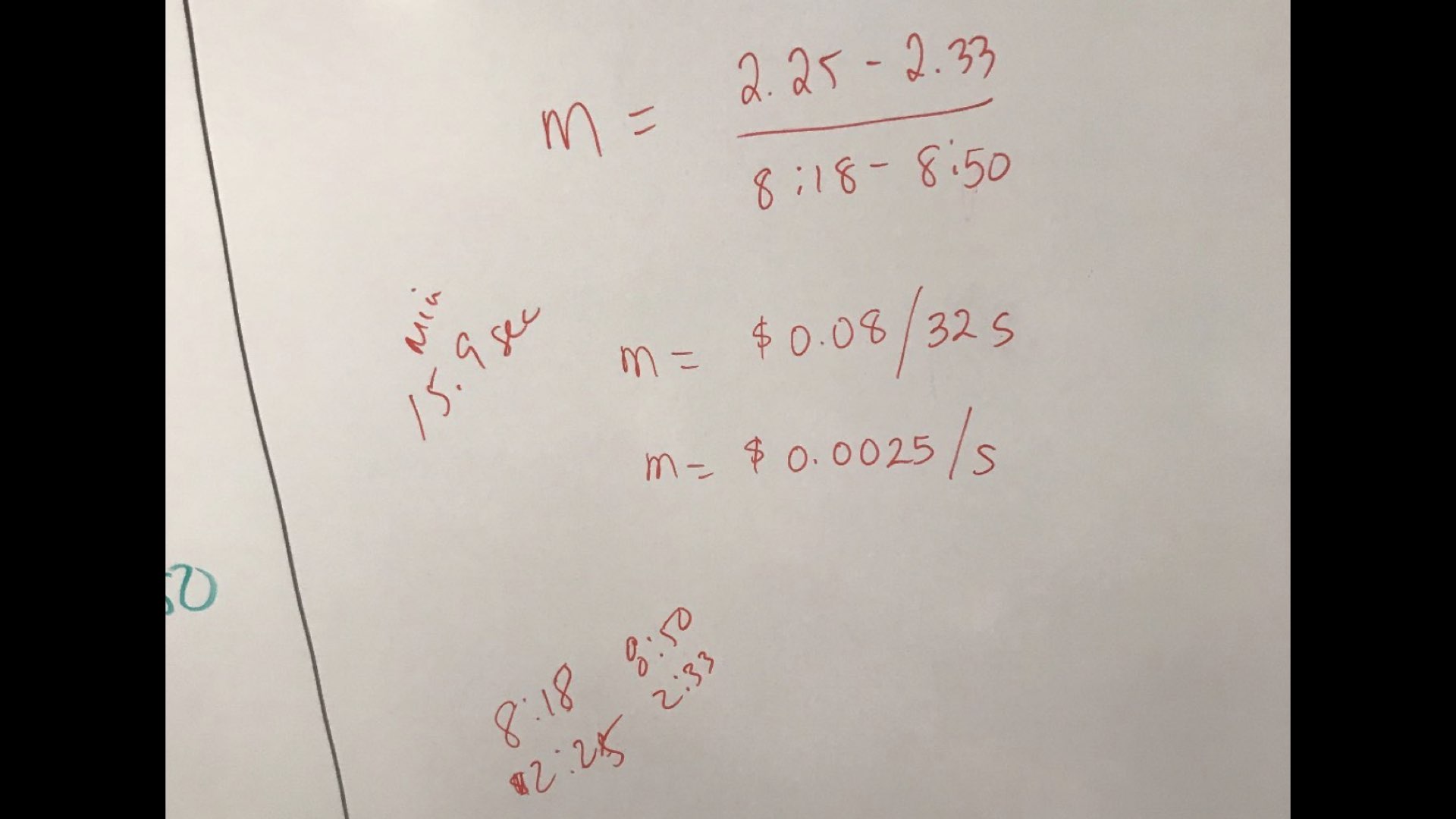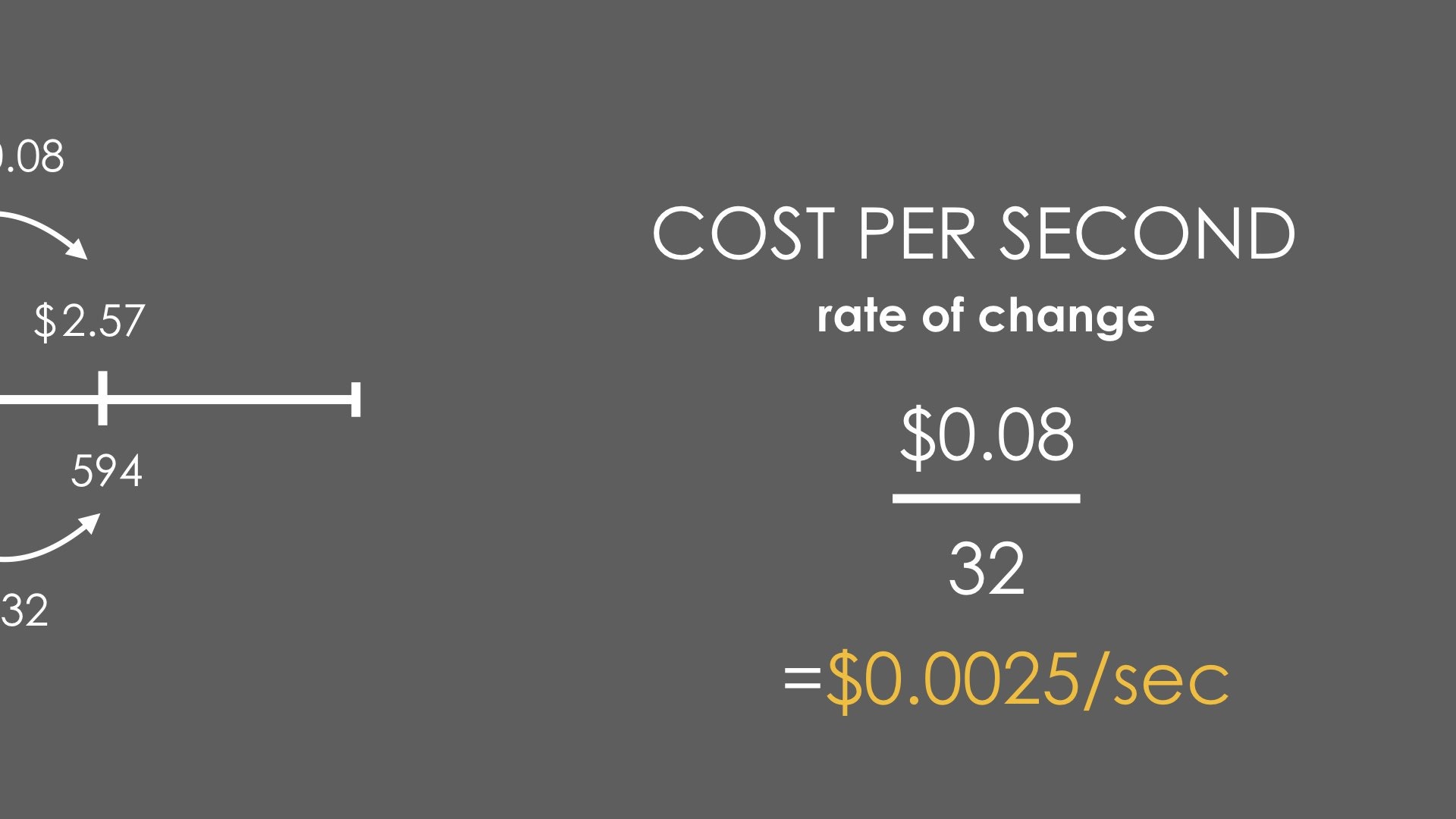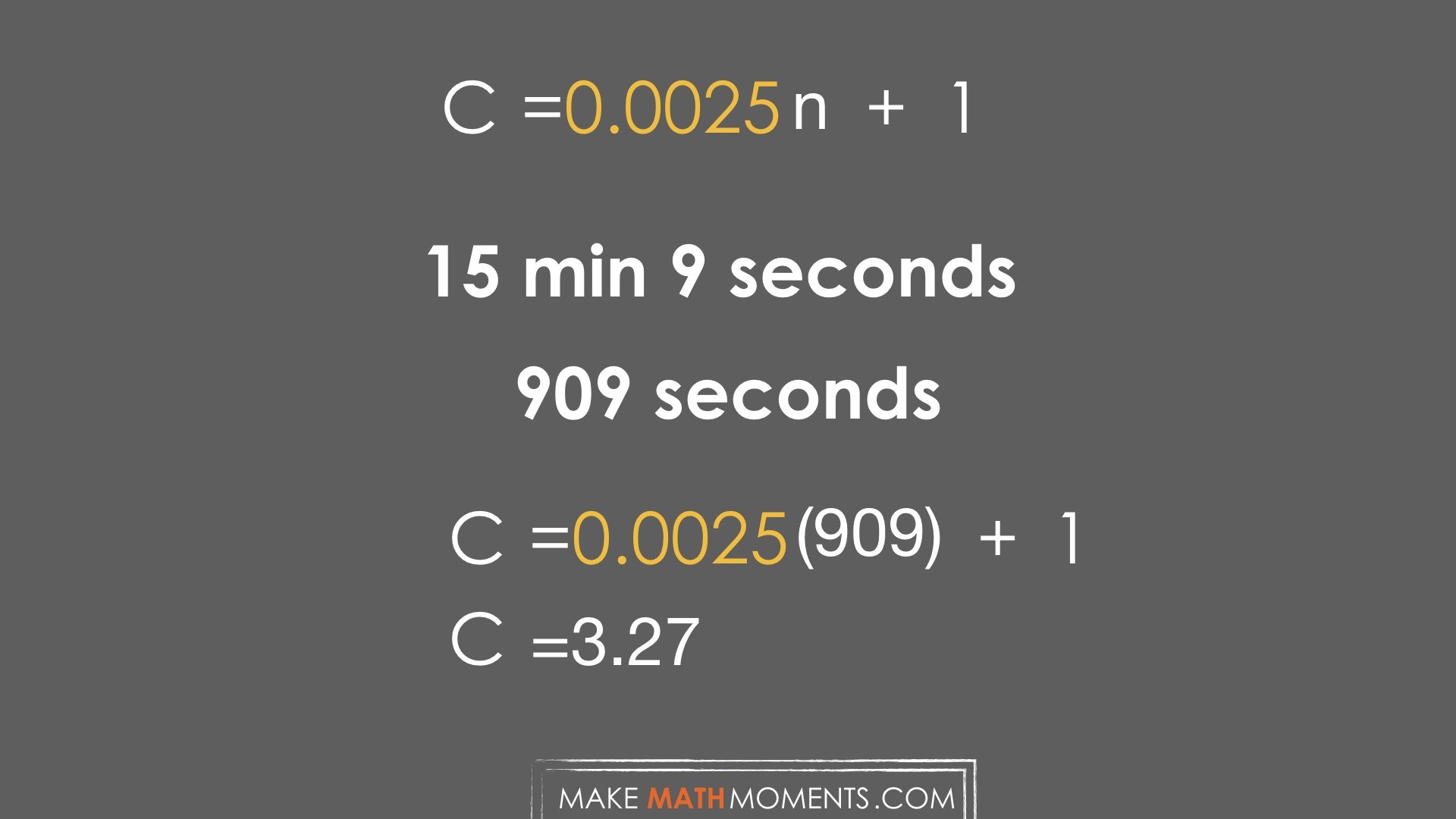NO BIKES ALLOWED
LINEAR RELATIONS
Make connections across representations of linear relations and determine the equation given two points.
Intentionality
Spark Curiosity
Fuel Sensemaking
During Moves
Student Approaches
Next Moves
Consolidation
Reflect and Consolidation Prompts
Resources & Downloads
Educator Discussion Area
Intentionality & Unit Overview
Current Length of Unit: 1 Day*
*This lesson is the first of an expected 5-day unit. The remaining four (4) days will be released as soon as they are available.
Students will extend their use of patterning to connect different representations of linear relations. More specifically, students will be exposed to rates of change, calculating the slope of a linear relation, building linear equations, and solving linear equations.
The purpose of this Task is:
- to help students develop an understanding of how various representations of linear relations are connected;
- create a linear equation given two points; and,
- solve linear equations.
There is a version 2 of this task that shows students a clear initial value. If you’d prefer that version look to the resources on this page.
Intentionality…
The mathematical ideas we are intentionally drawing out involve connecting various representations of linear relations, building linear equations from two or more points, and solving linear equations.
This will be achieved by first having students watch how the cost of renting a scooter is related to the time rented. You can learn more about the actual scooters and the pricing structure at lyft.com.
Spark Curiosity
What Do You Notice? What Do You Wonder?
Show students this video:
Ask students to engage in a notice and wonder protocol. ANYTHING and EVERYTHING that comes to mind is fair game.
Here’s some of the “everything and anything” students noticed and wondered on chart paper:
- I noticed that they were riding scooters;
- I noticed that they weren’t wearing helmets;
- I noticed the map;
- I noticed that the cost changes;
- I wonder where that was?
- I wonder how much the scooters cost?
- I wonder what the range means?
Prompt: Estimate
Now we can focus in on the big question for this task:
How much does it cost to ride the scooter the entire length of the outlined route?
We can now ask students to make an estimate using their reasoning skills. Asking students to think about quantities that would be too high and too low to be realistic is always helpful for students to set a reasonable range.
Students will also be uncomfortable here because the length of time of the trip or how the scooter charges customers has not been revealed yet. We encourage you to hold off on revealing these answers because it will build anticipation. This anticipation is what helps develop a high level of curiosity and almost naturally encourages students to want to start formulating a plan.
More Information
At this point, we want to give students the opportunity to improve their estimates by engaging in developing a problem solving strategy.
Ask students:
If we are going to improve our estimates, what information will we need?
Take a minute to think independently and then discuss your thoughts with an elbow partner.
After students have been given some time to think independently, instruct the students to turn and talk with elbow partners.
As the conversation gains momentum in the room, ask students to begin sharing out to the class.
While it might feel like you are cutting discussions short, waiting until the discussions end will mean less students will be eager to share with the whole group.
As students voice the information they wish to see, ask them:
What would you do with that information if we were able to share that with you?
Listen closely here as their responses give you important formative assessment details about their prior knowledge and their thinking into how they might begin solving this problem.
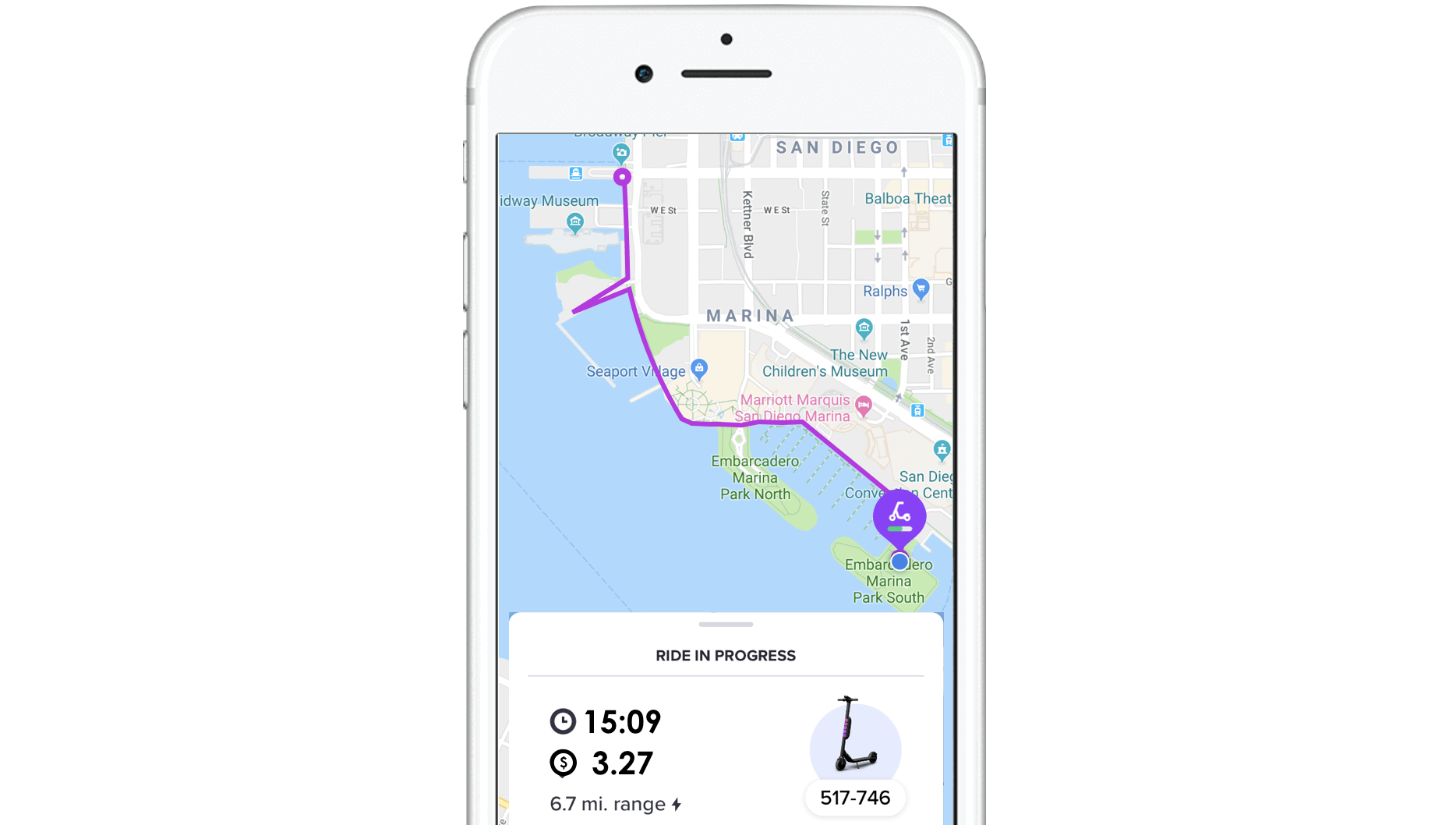
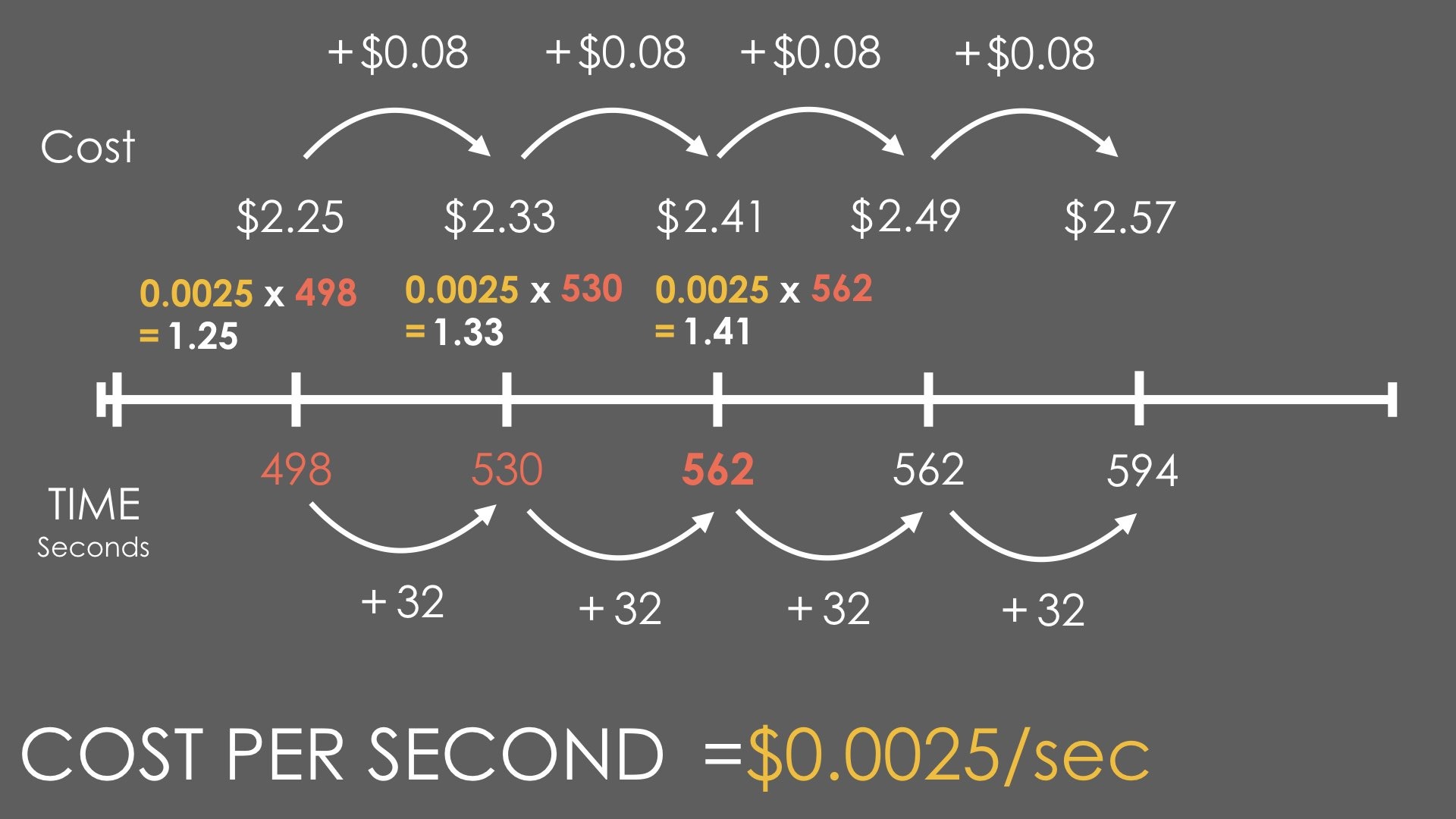
After students have shared their “information wishlist” and what they would use the information for, you can reveal this image of three (3) snapshots showing the cost at different times during the trip. 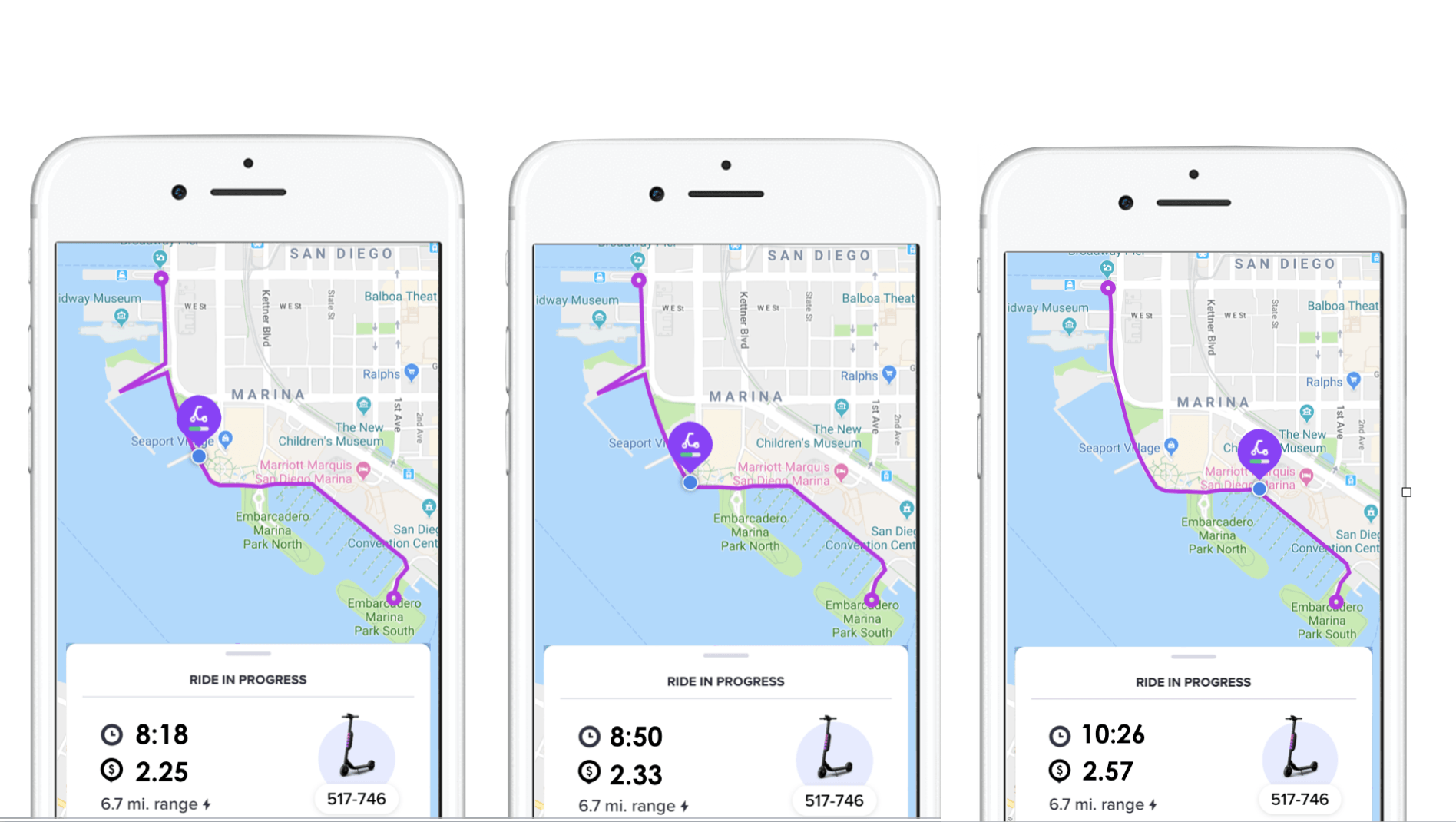
We have intentionally included three (3) points along the journey so that students can verify that the relationship between the cost and the time is linear.
Key Teacher Move:
If students explore the information given in the previous image, some will soon notice that not only does the cost of renting a scooter depend on the time the scooter has been rented for, but that there is also an initial value (i.e.: a flat fee) making this a partial variation (not directly proportional).
Fuel Sense-making
Prompt: Update Your Estimate
As students are discussing the implications of the cost and time at three (3) points along the journey, you can ask them to update their estimates with the following information:
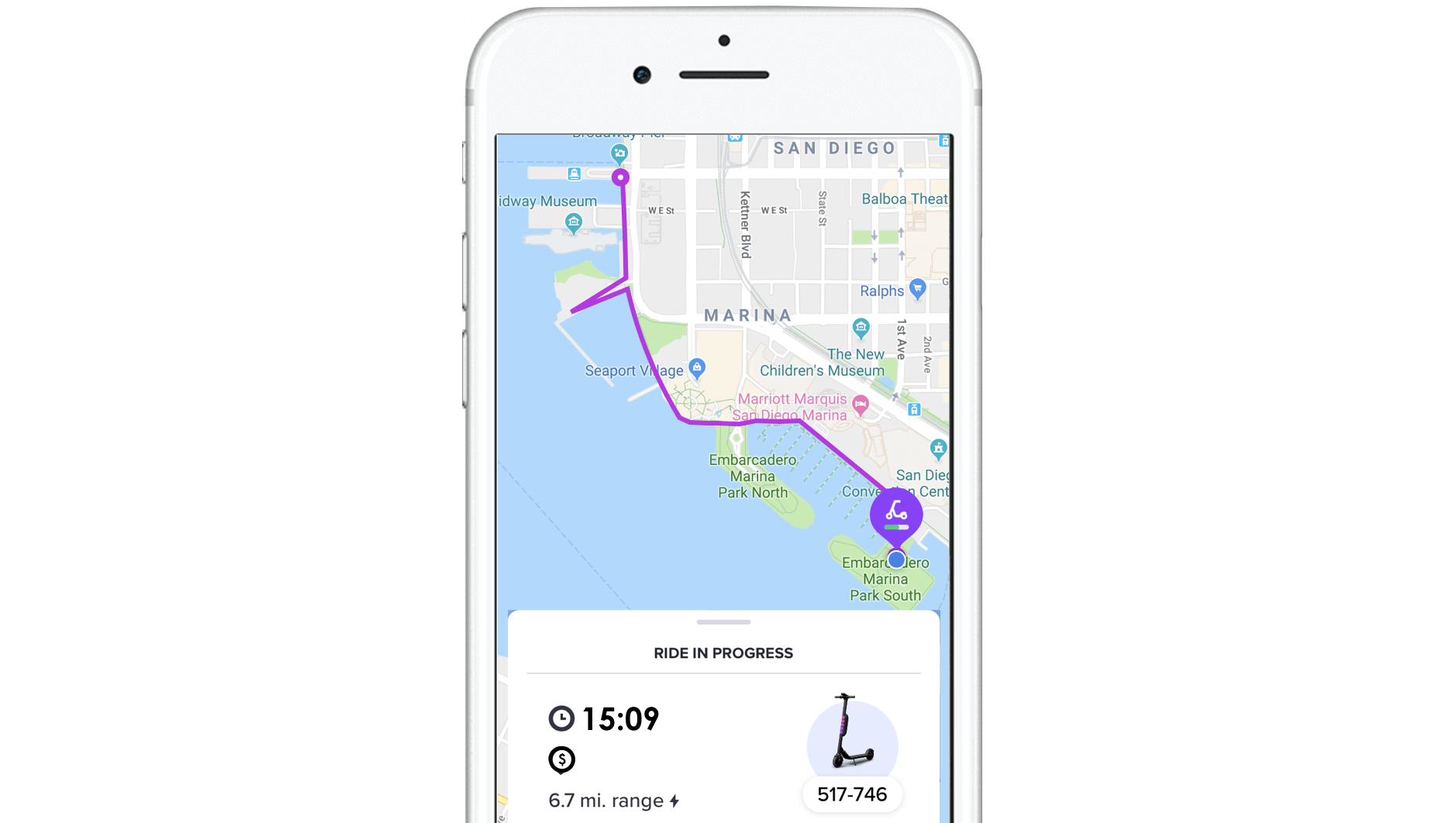
How much did the trip cost if we know the duration was 15 minutes and 9 seconds?
Image: Route & Total Time
Along with the previous prompt, you can share this image outlining the trip and the total time of the trip.
*Note that the cost of the trip is missing here.
During Moves
While Students Are Productively Struggling….
Monitor student thinking by circulating around the room and listening to the mathematical discourse. Select and sequence some of the student solution strategies and ask a student from the selected groups to share with the class from:
- most accessible to least accessible solution strategies and representations;
- most common/frequent to least common/frequent strategies and representations; or,
- choose another approach to selecting and sequencing student work.
Some of the mathematical models students might use as tools for thinking and/or to representat their thinking as they convince their peers and/or the teacher include:
- Times and associated costs written in what appears to be a disorganized manner.
- Double number line.
- Table of values.
- Graph.
- Student generated slope formula.
Have students share their strategies and reasoning for determining the total cost that can be expected after a certain length of time. Ask them to convince you and their peers that their thinking is correct by reasoning and proving using their selected strategies and mathematical models.
Discuss their strategies and elicit student thinking during your consolidation to build off of their current prior knowledge and understanding rather than “fixing” or “funnelling” student thinking to a strategy and/or model that does not connect to their strategy and/or approach. In order to anticipate what approaches students might take to solve this problem, some sample responses are included below.
Facilitator Note:
Some students will work primarily in seconds, others will work in minutes, and others still will use a combination of both. Keep a watch for students who fall for the common misconception that 15 minutes and 9 seconds is equivalent to 15.9 minutes.
Student Approaches
Student Approach #1: Misconception Assuming Proportional Relationship
Some students will mistakenly assume that the cost is directly proportional to the time, not noticing or ignoring the flat fee charged just to begin the trip.
A student might divide 2.25 by 530 and reveal a rate unrelated to this particular linear relationship. Help students reason through this misconception by asking:
Does it makes sense that the scooter is charging different rates at different times?
What else could be going on in this situation?
Student Approach #2: Double Number Line
Student Approach #3: Table of Values
Some students will create a table of values to study how the cost changes. Encourage students to look for a pattern which ultimately will help them get closer to recognizing that there is a constant rate that we can leverage here.
Student Approach #4: Student Generated Slope Formula
Assuming you are using this task to introduce the idea of an indirect linear relationship, this would mean that students do not have experience with the formula for slope of a line.
This does not mean that some students won’t be able to generate their own approach for finding the rate of change.
For example, students might notice that the three (3) points along the trip are:
Time Cost ($)
8m 18s 2.25
8m 50s 2.33
10m 26s 2.57
or
Time (s) Cost ($)
498 2.25
530 2.33
626 2.57
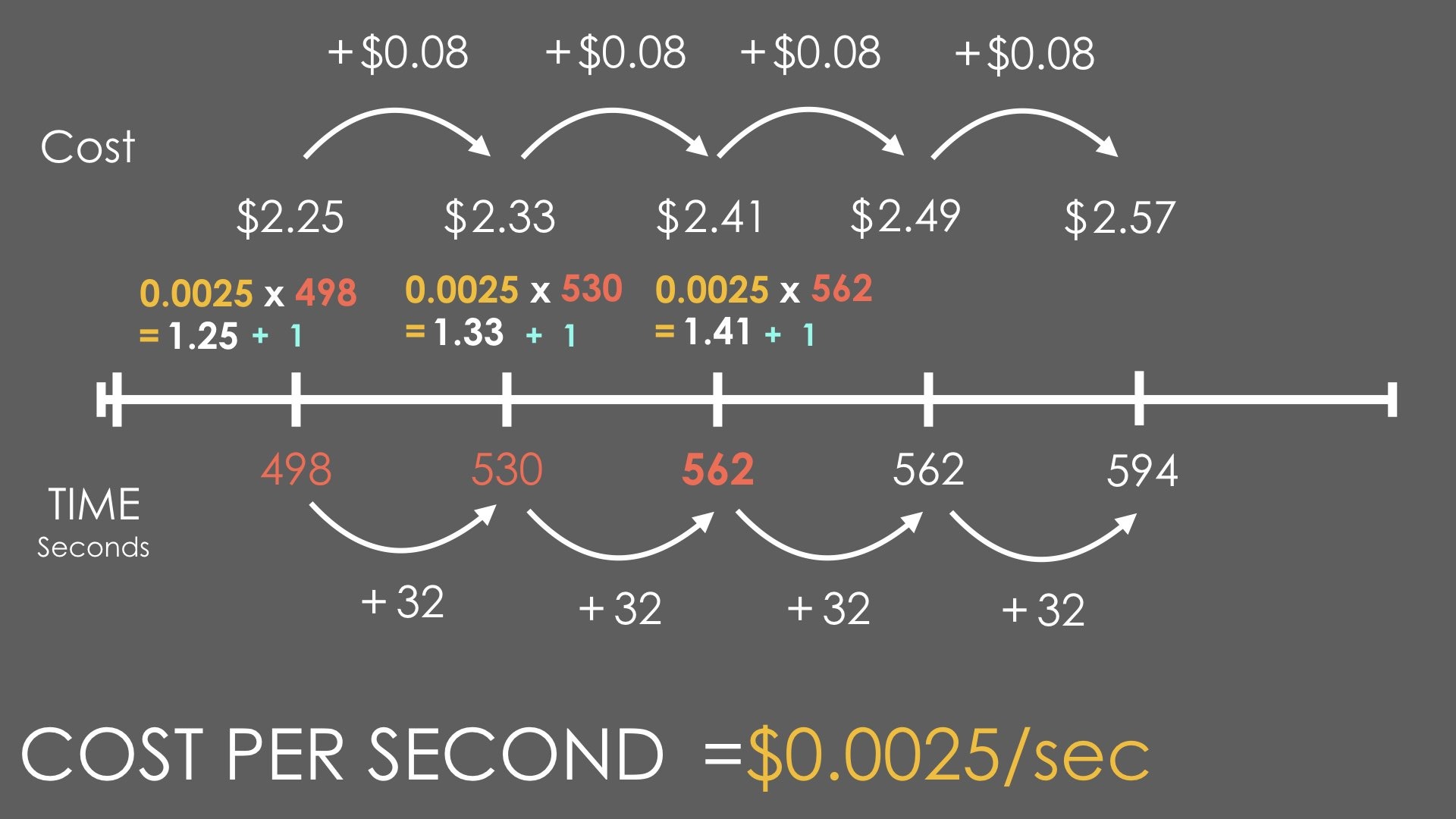
For students who realize that this is infact linear with a flat fee or initial value, they might notice that by subtracting any two costs and subtracting their corresponding times from the trip, they will have found the increase in cost over a certain length of time in the trip.
For example, finding the distance between $2.25 and $2.33 as well as 498 seconds and 530 seconds tells us how much the cost increased over a period of time along the journey:
The cost increased by $0.08 over a 32 second time period. Students might use a halving strategy to realize that it would be $0.04 in a 16 second time period or $0.02 in a 8 second time period or $0.01 in a 4 second time period. This is a rate of 4 seconds on the scooter per penny (or $0.0025 per second)
Or, we could scale up by a factor of 15 and get:
$0.60 per 60 seconds
or
$0.60 per minute
From here, students can use this information to determine the initial cost to start the trip.
If you’ve explored non-proportional linear relationships, some students might know the slope formula and put it to use to determine the cost per second or cost per minute:
Next Moves
Reveal
After consolidating learning using student generated solution strategies and by extending their thinking intentionally, we can share what the actual cost of the trip was:
Alternate Version
You can use this alternate version of the task to show the beginning of the trip.
The purpose behind this alternate is show that there is a clear initial value.
From there students can determine the rate of change (slope) and use it to build an equation.
Consolidation
During the consolidation, use student generated solution approaches and strategies to facilitate a discussion intended to connect student approaches to different representations of this linear relation such as the double number line, table, graph, and even the equation.
For example, students who have drawn a number line to demonstrate how the relation changes might have something like this:
On their own or through purposeful questioning from the teacher, students might be able to find a rate.
Students who have found the cost per second will still notice that simply multiplying the cost per second by the number of second will not get us the cost in the table. Something else is going on here.
Some other value that consistently needs to be added: the initial value or fixed cost.
Have a discussion at what this fixed cost could be and why there is one in this situation (Overhead costs? Rental fee? Cost per transaction, etc.)
To make connections among linear representations we want to show how the rate and initial value in this representations relates to the table and graph.
Some students may represent this pattern as a table instead of a double number line. Depending on your grade level you may also want to use the word slope to represent the cost per second.
With this new calculation rule students can move on to verify that it does indeed work with the third time/cost pair given. They then can finally find the cost of 15 minutes and 9 second or (909 Seconds).
Reflect and Consolidation Prompts
Provide students an opportunity to reflect on their learning by offering these consolidation prompts to be completed independently.
Consolidation Prompt #1:
In this lesson, there was an upfront cost to renting the scooter known as an initial value.
How might you recognize that a linear relationship has an initial value when looking at a table, graph, or equation?
Give an example.
Consolidation Prompt #2:
Finding a rate of change wasn’t as easy as looking at the increase in cost in the table or on a graph.
Explain how you found the rate and how you could use that strategy to find the rate in another linear relationship?
We suggest collecting this reflection as an additional opportunity to engage in the formative assessment process to inform next steps for individual students as well as how the whole class will proceed.
Dive into some extensions with your students for purposeful practice around this particular concept.
Extend #1:
If Jamal rented the same scooter and paid $5.45 for a trip, how many minutes did he ride for?
Extend #2:
Choose a number of minutes for which it would be easy to determine the cost of the trip.
Choose a number of minutes for which it would be hard to determine the cost of the trip.
Find the costs of those trips and explain why the first was easy and the second was more difficult.
Extend #3:
Create your own pricing structure for renting scooters.
Create a table and equation to represent how the cost relates to the number of seconds travelled.
Resources & Downloads
Printable Lesson Plan PDF
Videos, Images & Media Files
Apple Keynote Presentation
Powerpoint Presentation
Printable Consolidation Prompts
Optional Worksheet
Educator Discussion Area
Login/Join to access the entire Teacher Guide, downloadable slide decks and printable handouts for this lesson and all problem based units.
Explore Our 60+ Problem Based Units
This Make Math Moments Lesson was designed to spark curiosity for a multi-day unit of study with built in purposeful practice, number talks and extensions to elicit and emerge strategies and mathematical models.
Dig into our other units of study and view by concept continuum, grade or topic!