JUST KEEP DIGGING
MULTIPLYING AND DIVIDING INTEGERS
Dive into this 5-Day Problem Based Math Unit focused on solving situations involving multiplication and division of positive and negative integers.
Intentionality
Spark Curiosity
Fuel Sensemaking
During Moves
Student Approaches
Next Moves
Consolidation
Reflect and Consolidation Prompts
Resources & Downloads
Educator Discussion Area
Intentionality & Unit Overview

Length of Unit: 5 Days
Access each lesson from this unit using the navigation links below
Students will model multiplication and division contexts involving positive and negative integers in order to solve.
Intentionality…
In this task, students will represent multiplication as repeated equal groups of a single quantity (or quota). In today’s context, the repeated equal group is a negative rate of feet per hour. Students will then use quotative division to determine how many groups of the negative rate are in a total quantity. Some of the big ideas revealed in today’s lesson include:
- Multiplication can be understood as repeated equal groups;
- The first factor can be understood as the number of groups and the second factor as the size of the groups;
- A positive integer multiplied by a negative integer has a product that is negative;
- Quotative division is when the total quota is known (the dividend), and the number per group or the rate (the divisor) is known;
- Quotative division reveals the number of copies or iterations of a rate that can be derived from the overall quota (the dividend);
- A negative number divided by a negative number has a quotient that is positive.
Spark Curiosity
What Do You Notice? What Do You Wonder?
Show students the following video:
Then, ask students:
What do you notice?
What do you wonder?
Give students 60 seconds (or more) to do a rapid write on a piece of paper.
Replaying the video can be helpful here.
Then, ask students to share with their neighbours for another 60 seconds.
Finally, allow students to share with the entire group.
Some of the noticing and wondering that came up in a class recently included:
- I notice dirt
- I notice someone digging.
- I notice the dig 4 feet down every hour.
- I wonder how long they will dig.
- I wonder how deep they will go.
- I wonder why they are digging.
- I notice there is a scale.
At this point, you can answer any notices and wonders that you can cross off the list right away. Confirm for students that this person is digging a hole for a new well. He appears to be digging at a rate of -4 feet per hour.
Estimation: Prompt
Next, share the following visual prompt briefly and ask the following question:
If digging continues at the same rate for 6 hours, how would you describe the depth of the hole?
Give students an opportunity to turn and talk. We want students to communicate that the depth can be described as -24 feet. The purpose of this estimation is to build confidence with the use of negative integers to describe measurements.
Estimation: Reveal
Share the following image revealing the total depth after 6 hours of digging at a rate of -4 feet per hour.
Share the following prompt:
How could we represent this situation as an equation?
The purpose of this estimation is to help students see that this scenario can be represented as a multiplication.
For example,
6 hours x (-4 feet/hour) = -24 feet
or
6 x (-4) = -24
Here is a visual of this thinking:
Fuel Sense-making
Crafting A Productive Struggle: Prompt
Since you have already taken some time to set the context for this problem and student curiosity is already sparked, we have them in a perfect spot to help push their thinking further and fuel sense making.
Share the following prompt.
The well needs to be -56 feet to reach groundwater. Assuming he continues digging at a rate of -4feet/hour, how long will it take to dig this well?
During Moves
While Students Are Productively Struggling…
Monitor student thinking by circulating around the room and listening to the mathematical discourse. Select and sequence some of the student solution strategies and ask a student from the selected groups to share with the class from:
- most accessible to least accessible solution strategies and representations;
- most common misconceptions;
- most common/frequent to least common/frequent representations; or,
- choose another approach to selecting and sequencing student work.
The tools and representations you might see students using to convince their peers and/or the teacher include:
- Skip Counting;
- Using repeated addition;
- Using repeated subtraction;
- Using partial quotients;
- Using partial products;
- Using a standard algorithm.
Have students share their reasoning for determining the total number of hours. Discuss their thinking during your consolidation to build off of their current prior knowledge and understanding rather than “fixing” or “funnelling” student thinking to a representation and justification that does not connect to their understanding.
Student Approaches
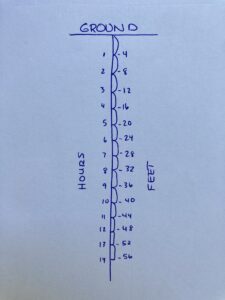
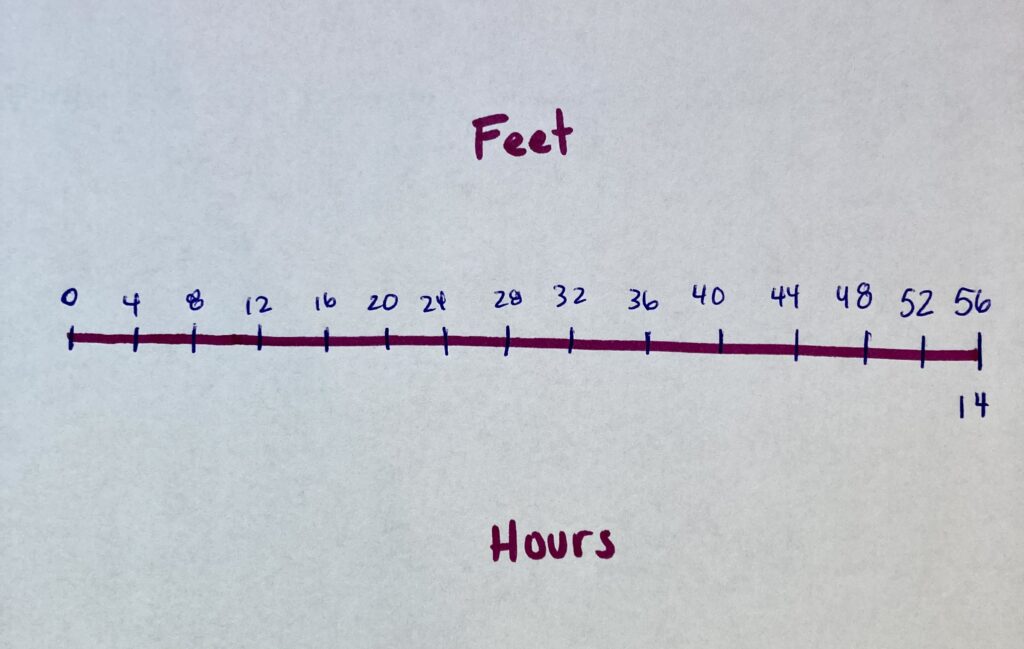
Student Approach #1: Using Repeated Addition on a Double Numberline
I started at the ground level. I kept adding -4 feet one group at a time until I got to a total of -56 feet. That was 14 jumps altogether, so 14 hours.
Student Approach #2: Using Repeated Subtraction on a Double Number Line
I started at -56 feet on a numberline. I subtracted -4 feet until I got to 0. I had to do that 14 times, so that means it will take 14 hours to dig the well.
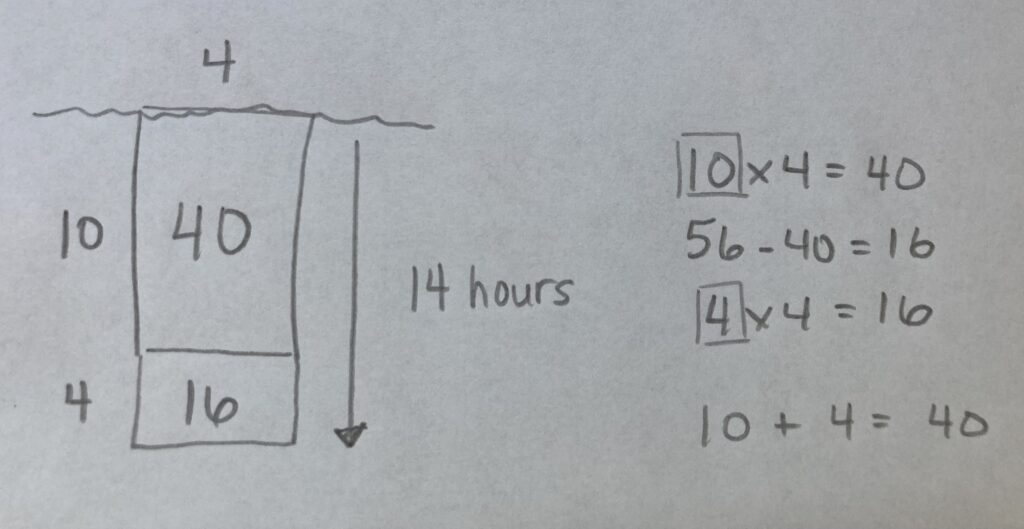
Student Approach #3: Using Partial Products
I know I have to find out how many groups of -4 are in -56. I know that there are 10 groups of -4 in -40, because 10 x -4 = 40. That left me with -16. And 4 x -4 is -16, so 10 plus 4 is a total of 14 hours.
Next Moves
Reveal
The big ideas in this introductory lesson are:
- A positive integer multiplied by a negative integer has a product that is negative;
- A negative number divided by a negative number has a quotient that is positive.
In today’s task, students were asked to divide -56 by -4. This context is an example of quotative division.
Use student solutions to explore a variety of ways to determine the quotient of this division scenario.
Students may not realize that they were actually dividing. This scenario is an example of quotative or measured division.
- Quotative division is when the total quota is known (-56 feet), and the number per group or the rate (-4 feet per hour) is known;
- Quotative division reveals the number of copies or iterations of a rate (the number of hours) that can be derived from the overall quota;
During the consolidation, solidiy student understanding that this context can be represented as:
(-56 feet) x (-4feet/hour) = 14 hours
Hopefully through this context, students will be able to justify why the results (the quotient) is positive.
Consolidation
The big ideas in this introductory lesson are:
- A positive integer multiplied by a negative integer has a product that is negative;
- A negative number divided by a negative number has a quotient that is positive.
In today’s task, students were asked to divide -56 by -4. This context is an example of quotative division.
Use student solutions to explore a variety of ways to determine the quotient of this division scenario.
Students may not realize that they were actually dividing. This scenario is an example of quotative or measured division.
- Quotative division is when the total quota is known (-56 feet), and the number per group or the rate (-4 feet per hour) is known;
- Quotative division reveals the number of copies or iterations of a rate (the number of hours) that can be derived from the overall quota;
During the consolidation, solidiy student understanding that this context can be represented as:
(-56 feet) x (-4feet/hour) = 14 hours
Hopefully through this context, students will be able to justify why the results (the quotient) is positive.
Reflect and Consolidation Prompts
Provide students an opportunity to reflect on their learning by offering these consolidation prompts to be completed independently.
Consolidation Prompt #1:
A negative integer divided by a negative integer is positive. Justify this statement.
Consolidation Prompt #2:
Solve:
a. 7 x (-3)
b. 9 x (-8)
c. -55 ÷ (-5)
d. -42 ÷ (-6)
We suggest collecting this reflection as an additional opportunity to engage in the formative assessment process to inform next steps for individual students as well as how the whole class will proceed.
Resources & Downloads
Educator Discussion Area
Login/Join to access the entire Teacher Guide, downloadable slide decks and printable handouts for this lesson and all problem based units.
Explore Our 60+ Problem Based Units
This Make Math Moments Lesson was designed to spark curiosity for a multi-day unit of study with built in purposeful practice, number talks and extensions to elicit and emerge strategies and mathematical models.
Dig into our other units of study and view by concept continuum, grade or topic!