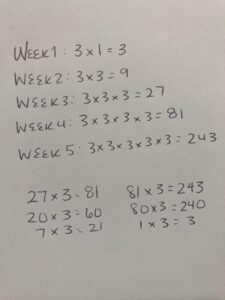INVASIVE SPECIES
EXPONENTIAL GROWTH & DECAY
Through the context of invasive species growth and the use of patterning, students will analyze the relationship between the size and unit of an exponent and the value of a power.
Intentionality
Spark Curiosity
Fuel Sensemaking
During Moves
Student Approaches
Next Moves
Consolidation
Reflect and Consolidation Prompts
Resources & Downloads
Educator Discussion Area
Intentionality & Unit Overview

Length of Unit: 5 Days
Access each lesson from this unit using the navigation links below
Students will investigate the pattern of growth of an invasive plant, the Giant Hogweed, that continues to grow at an exponential rate.
In this task, students will analyze the growth of the Giant Hogweed plant, an invasive species. They will record the data, determine the pattern rule, and make predictions about the pattern. Some of the big ideas that may emerge in this task include:
- Patterns can be extended because they are repetitive by nature.
- Pattern rules are generalizations about a pattern, and they can be described in words.
- One common use of patterns is predicting future events.
- A pattern can be extended to make a prediction.
- For far predictions, calculations are required for efficiency.
- Exponential growth is a pattern of data that shows greater increases with passing time.
- In a power, the base number is defined as a number which is multiplied by itself.
- In a power, the exponent represents the number of times the base number is multiplied.
- When a pattern is growing exponentially, the variable representing time is the exponent.
- Graphical representations of exponential growth appear as a curved line.
Spark Curiosity
What Do You Notice? What Do You Wonder?
Show students the following video:
Then, ask students:
What do you notice?
What do you wonder?
Give students 60 seconds (or more) to do a rapid write on a piece of paper.
Replaying the video can be helpful here.
Then, ask students to share with their neighbours for another 60 seconds.
Finally, allow students to share with the entire group. Be sure to write down these noticings and wonderings on the blackboard/whiteboard, chart paper, or some other means to ensure students know that their voice is acknowledged and appreciated.
Some of the noticing and wondering that may come up includes:
- I notice dirt or the ground, maybe a garden.
- I notice on week 0, there was one plant.
- I notice on week 1, there are three plants.
- I notice on week 2, there are 9 plants.
- I wonder how many plants there will be on week 3.
- I wonder if there will be six more plants every time.
- I wonder if the growth is the same every week.
Estimation: Prompt
After we have heard students and demonstrated that we value their voice, we can land on the first question we will challenge them with:
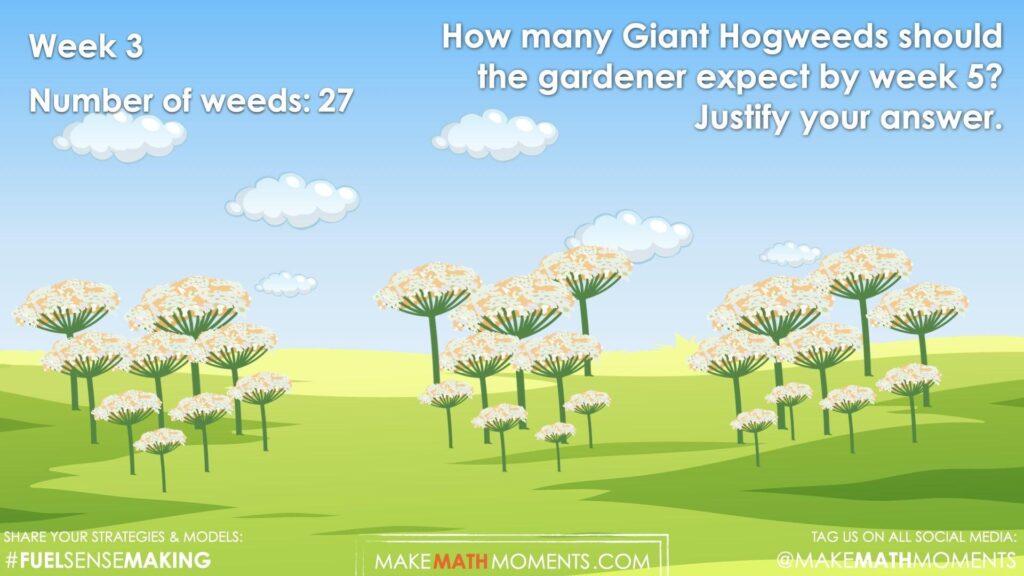
How many weeds will appear in the garden on week 3?
Sharing the video a second time could be helpful.
We can now ask students to make an estimate (not a guess) as we want them to be as strategic as they can possibly be. This will force them to determine a number of weeds through reasoning. Give them a chance to discuss with a partner before sharing their answer with the larger group. Some students may view this pattern as linear, add six, while others may recognize that each weed is being replaced by an additional three weeds every week.
Estimation: Reveal
Show students the following video.
Here is a screenshot of the final frame of the video.
Fuel Sense-making
Crafting A Productive Struggle: Prompt
Giant hogweed is an extremely invasive species that originated from Asia and Eastern Europe. An invasive species is an organism that is not native to an ecosystem and causes harm to the environment. The weed has taken over this patch of garden.
If the gardener does not intervene, predict how many Giant hogweeds she will find in her garden in 5 weeks. Justify your answer.
A screenshot of the final frame in the Struggle Prompt Video can be found below:
During Moves
While Students Are Productively Struggling…
Monitor student thinking by circulating around the room and listening to the mathematical discourse. Select and sequence some of the student solution strategies and ask a student from the selected groups to share with the class from:
- most accessible to least accessible solution strategies and representations;
- most common/frequent to least common/frequent strategies and representations; or,
- choose another approach to selecting and sequencing student work.
The tools and representations you might see students using to convince their peers and/or the teacher include:
- Counting on
- Addition
- Multiplication
- Partial Products
- Modelling
Have students share their strategies and reasoning for how to represent the number of weeds in 5 weeks. Ask them to convince you and their peers that their answer is correct by sharing mathematical models.
Discuss their strategies and elicit student thinking during your consolidation to build off of their current prior knowledge and understanding rather than “fixing” or “funnelling” student thinking to a strategy and/or model that does not connect to their strategy and/or approach.
Student Approaches
Student Approach #1: Counting in a Pictorial Model
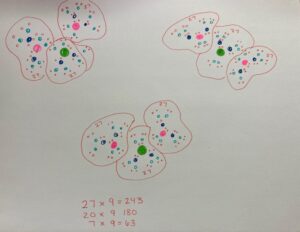
I drew what was happening in the video. Every week one weed turns into three weeds. I did this for five weeks, every week using a new colour to see the new weeds that had grown. Once I was done, there were two many weeds to count without making a mistake. So I circled clusters. There were 27 in each cluster, and nine clusters. Nine multiplied by 27 is 243 weeds altogether.
Student Approach #2: Tree Diagram
I knew that there would be a lot of weeds by week 5. I drew the first weed turning into three, and then I just focused on one of the three weeds from week one. I used a tree diagram to continue changing every weed into three weeds as time went on. I realized that one of the three weeds in week one became 81 weeds by week 5. I added 81 + 81 + 81, which gave me 243 weeds altogether.
Student Approach #3: General Term
I notice that on week 1, there are 3. So the number of weeds is three one time. But in week two, the number of weeds is 3 x 3, because 3 weeds became 9 weeds. And by week three, it was 3 x 3 x 3, or nine x three, because each weed became three weeds once again. I figured there must be a rule. I think the rule is however many weeks go by, that’s the number of times you multiply three by itself. So on week five, it must be 3x3x3x3x3, one three for every week. I multiplied 3 by itself five times, and the answer is 243 weeds.
Next Moves
Consolidation
Consolidate your intentionally selected student solutions. Look for similarities in students’ approaches along the developmental continuum. For this task, pictorial representations are likely most accessible for all learners.
Consider how students went about extending this pattern or using calculations to predict the number of weeds by week 5.
Students likely noticed that the number of weeds grew three times greater every week. In other words, the scale factor or multiplicative comparison from one week to next was consistently 3 times greater.
Help students make a generalization about this pattern by considering the relationship between the number of weeks and the number of weeds.
Share the information in a table to develop a generalization.
Viewing the following consolidation video will help you with planning and delivering an effective consolidation for this lesson:
Ask students:
What do we know about this pattern?
On week 1, we have 1 group of 3, (3)
On week two, we have 3 groups of 3, 3 x (3)
On week three, we have three groups three groups of 3, 3 x (3 x 3)
Ask students to generalize this pattern. Look at the number of threes in the multiplication sentence relative to the number of weeks.
Help students land on the idea that the initial value is one and the base number in this context is three.
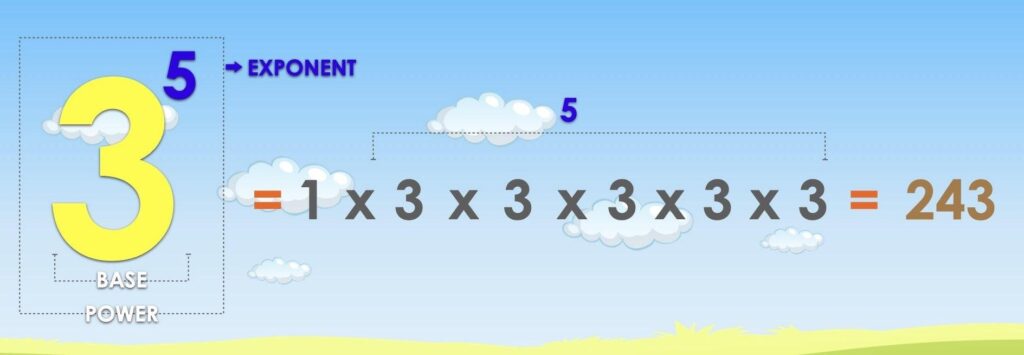
The number of times that we multiply the base by itself (how many times to use the number in a multiplication) is determined by the number of weeks (time), which is represented by an exponent.
This relationship can be represented as an expression using exponential notation, y = 1 x \(3^x\).
The number of weeds = the initial number of weeds x the base (3) to the exponent (the number of weeks)
Ask students to write an equation for the number of weeds on week 6.
number of weeds = 1 weed x (3 x 3 x 3 x 3 x 3 x 3)
or
number of weeds = 1 x \(3^6\)
Reflect and Consolidation Prompts
Provide students an opportunity to reflect on their learning by offering these consolidation prompts to be completed independently.
Consolidation Prompt #1:
Today we explored an expression where three (3) is the base and the exponent is the number of weeks. Describe the word base and exponent in this context.
Consolidation Prompt #2:
Consider the pattern below. Describe the pattern rule in words. Extend the pattern to day 5.
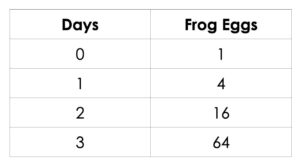
We suggest collecting this reflection as an additional opportunity to engage in the formative assessment process to inform next steps for individual students as well as how the whole class will proceed.
Resources & Downloads
Printable Lesson Plan PDF
Educator Discussion Area
Login/Join to access the entire Teacher Guide, downloadable slide decks and printable handouts for this lesson and all problem based units.
Explore Our 60+ Problem Based Units
This Make Math Moments Lesson was designed to spark curiosity for a multi-day unit of study with built in purposeful practice, number talks and extensions to elicit and emerge strategies and mathematical models.
Dig into our other units of study and view by concept continuum, grade or topic!