GUMMY WORMS
SUBTRACTION
Uncover the various subtraction structures including removal, conparison, missing, addend, and missing subtrahend.
Intentionality
Spark Curiosity
Fuel Sensemaking
During Moves
Student Approaches
Next Moves
Consolidation
Reflect and Consolidation Prompts
Resources & Downloads
Educator Discussion Area
Intentionality & Unit Overview

Length of Unit: 5 Days
Access each lesson from this unit using the navigation links below
Students will estimate the number of gummy worms in the jar.
In this task, students will explore the concept of quantity through estimation using their spatial reasoning skills.
Full Video Walk-Thru
Watch the full video walk-thru below to get a sense of how you might deliver this task:
Spark Curiosity
What Do You Notice? What Do You Wonder?
Show students this video:
Then, ask students:
What do you notice?
What do you wonder?
Give students 60 seconds (or more) to do a rapid write on a piece of paper.
Then, ask students to share with their neighbours for another 60 seconds.
Finally, allow students to share with the entire group.
Some of the noticing and wondering that came up in a class recently included:
- Jar is half full.
- How many gummy worms are there?
- There are at least two different kinds of gummy worms in the jar.
- Are the gummy worms full or cut in half?
- There are two large rectangles and 4 squares along the bottom wall
- What does the tag say?
- How large is the jar?
- What kind of activity are we doing?
- Will we get some gummy worms to eat?
- and many more…
At this point, you can answer any notices and wonders that you can cross off the list right away. Things like “I wonder whether we will get any gummy worms?” can be addressed right away to show students that we are indeed listening to their noticing and wondering and that we value student voice.
Estimation: Prompt
After we have heard students and demonstrated that we value their voice, we can land on the first question we’ll challenge them with:
How many gummy worms are in the jar?
Follow up that question with:
How might we convince someone that the quantity you come up with is correct?
We can now ask students to make an estimate (not a guess) as we want them to be as strategic as they can possibly be. This will force them to use spatial reasoning alone to try and come up with an initial estimate and to share it with their neighbours by trying to articulate why they believe their prediction is reasonable.
Consider asking students to think about a number that would be “too low” and a number that would be “too high” before asking for their best estimate in order to help them come up with a more reasonable estimate.
Let them chat with their neighbours and challenge them to an estimation duel or a math fight.
While Students Are Estimating…
Monitor student thinking by circulating around the room and listening to the mathematical discourse.
Encourage students to use precise mathematical language (including greater than, less than, more, less, half, rows…) and positional language (in front, behind, on top…) to articulate their defense.
If students’ estimates are unreasonable, encourage them to select a manipulative similar in size to the gummy worms (perhaps a relational rod) and ask them to lay out that number of items in front of them to consider whether that quantity seems reasonable.
Reveal 1: Counting The Gummy Worms
After allowing students to share their estimates with neighbours and writing them down on the chalkboard/whiteboard/chart paper, let’s give them something to celebrate about with our first reveal:
Answer: 25 gummy worms.
Revisit the student answers. Ask students why their answers may or may not have been exact.
Celebrate the closest estimate in the way that you typically do in class. One such method might be doing a “1, 2, 3, CLAP!” for those who were closest.
Also make a special note to congratulate some of the students who weren’t so close and ensure that they know that we are building our estimation skills through this process.
Fuel Sense-making
Crafting A Productive Struggle: Prompt
Since we’ve already taken some time to set the context for this problem and student curiosity is already sparked, we have them in a perfect spot to help push their thinking further and fuel sense making.
Now that the context is already set, we’re good to start pushing the thinking and it is likely that any additional noticing or wondering will not be necessary at this point in the lesson.
Show them the following video where all of the gummy worms are placed back into the jar and then some are removed.
The question we’ll try to figure out is:
How many gummy worms are left in the jar?
Keep in mind, you can modify what question(s) you ask depending on what mathematical thinking you are looking to elicit. For example, you could also ask:
How many gummy worms were taken from the jar?
Having students estimate is always fun, but it is probably not necessary to have them estimate and share out at this stage like we did in the previous portion of the task. However, proceed or pivot as you see fit here.
In this task, students will have an opportunity to reason through a subtraction scenario. This particular problem is an example of the “removal” subtraction structure, often referred to as “take away”. This task will allow students to apply a variety of strategies and models, while developing a deeper understanding of big ideas, including the following;
- Part-whole relations: Relationships between addition & subtraction.
- One-to-one correspondence.
- One structure of subtraction is “removal”.
During Moves
While Students Are Productively Struggling…
Monitor student thinking by circulating around the room and listening to the mathematical discourse. Select and sequence some of the student solution strategies and ask a student from the selected groups to share with the class from:
- most accessible to least accessible solution strategies and representations;
- most common/frequent to least common/frequent strategies and representations; or,
- choose another approach to selecting and sequencing student work.
The tools and representations you might see students using to convince their peers and/or the teacher include:
- Concrete manipulatives such as connecting cubes, square tiles or relational rods to model and count the number of gummy worms after 8 have been removed.
- Use of number path, number line or number chart to count on or count back.
- Part-whole place mat to reveal the missing addend.
- Drawings or tally marks.
Have students share their strategies and reasoning for determining the gummy worms left in the jar. Ask them to convince you and their peers that their answer is correct by sharing mathematical models.
Discuss their strategies and elicit student thinking during your consolidation to build off of their current prior knowledge and understanding rather than “fixing” or “funnelling” student thinking to a strategy and/or model that does not connect to their strategy and/or approach.
Student Approaches
Student Approach #1: Concrete Materials & Counting 3 Time
“These are the gummy worms. There were 25 in the jar. I put them in groups of 5 just like in the video, see that’s 5, 10, 15, 20, 25 gummy worms. Then I saw that 8 were taken out of the jar. Here are the 8 that were taken out. So then I counted how many are left (1, 2, 3, 4, 5, 6 , 7, 8,….) and I counted 17.”
Strategy:
This student used concrete materials to represent the whole: 25 gummy worms. They removed 8 by counting one to one, and then counted the remaining gummy worms. This student used a “counting three times” strategy.
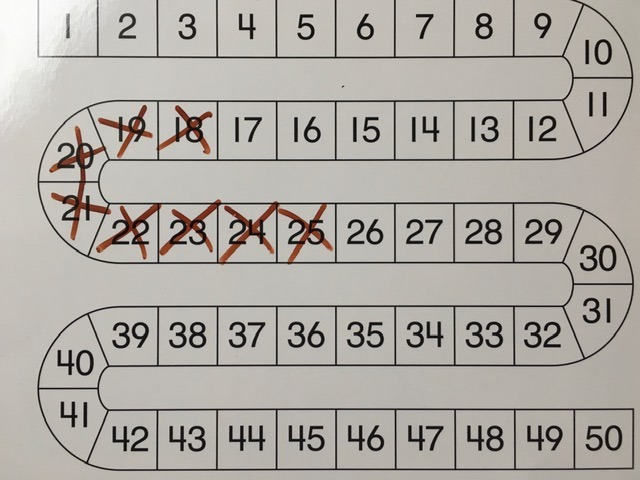
Student Approach #2: Number Path & Counting Back
“I know that there are 25 gummy worms in the jar. So I counted back and put an x on every gummy worm that was taken out of the jar. I see that there are 17 gummy worms still in the jar.”
Strategy:
This student used the number path to indicate the whole, 25 gummy worms in the jar. They counted back by ones 8 times to reveal 17 left.
Student Approach #3: Part Whole Mat & Friendly Numbers
“I used the part-part whole mat to write down what I know.
I know there are 25 gummy worms altogether because we saw that is the first video. I also saw that gummy worms were taken out of the jar and there are 8 on the counter. What I don’t know is how many are still in the jar. I have to figure out how many are left.
So I know that if there were 20 left, that would be 28 altogether, because 20 + 8 is 28. So I tried 19, that was too much. I saw that it was 2 too many gummy worms, so I knew it must be 17 gummy worms in the jar.”
Strategy:
This student used the part whole mat to identify the total number of gummy worms in the jar (25). They showed the two parts. The number of gummy worms removed and the number remaining in the jar. They used friendly facts and reasoning to add the two parts together and continued adjusting the number to reveal 17.
Next Moves
Reveal 2: How Many Are Left In The Jar?
After consolidating the learning by monitoring, selecting, and sequencing student work, have those students whose work will help expose different mathematical models. You can sequence in many ways, but a common method is from most accessible solution strategy to least accessible.
Then, share the second reveal video.
Answer: There are 17 gummy worms left in the jar
Revisit student answers and approaches.
Consolidation
Consolidate learning using student generated solution strategies based on what you selected and how you sequenced while monitoring during the Sense Making portion of the lesson.
The purpose of the consolidation is to generalize that one structure of subtraction is seperate or “take away”.
Reflect and Consolidation Prompts
More Subtraction Professional Learning
A common misconception that many of us have is that we must think of different contexts for different problems in each math class. However, this is simply not the case. Leverage the investment in doing the notice and wonder at the beginning of this lesson to allow you to squeeze out as much mathematical goodness as you can out of this single context. Students are all well aware of the context and now we can focus on the mathematical thinking.
Did you know that there are 4 types of addition and subtraction problems? Why not use this context as a way to ask questions that utilize the different types of addition and subtraction.
- Join – I had 18 gummy worms in the jar and I added 10 more. How many gummy worms do I have altogether?
- Separate – I had 25 gummy worms in the jar and I ate 10. How many did I eat?
- Part-Part-Whole – There are 13 gummy worms in one jar and 16 in another. How many gummy worms are there in total?
- Compare – One jar has 25 gummy worms while another has 18 gummy worms. How many more gummy worms does the first jar have?
There are even scenarios that we can build out within these structures such as:
- Missing Addend: There were 25 gummy worms and an extra package was added to the jar. There are now 32 gummy worms. How many were added?
- Missing Subtrahend: There were 25 gummy worms. Now there are 12 left in the jar. How many were eaten?
You can learn more about addition and subtraction structures in Module 4 of The Concept Holding Your Students Back mini-course.
Resources & Downloads
Printable Lesson Plan PDF
Videos, Images & Media Files
Apple Keynote Presentation
Powerpoint Presentation
Educator Discussion Area
Login/Join to access the entire Teacher Guide, downloadable slide decks and printable handouts for this lesson and all problem based units.
Explore Our 60+ Problem Based Units
This Make Math Moments Lesson was designed to spark curiosity for a multi-day unit of study with built in purposeful practice, number talks and extensions to elicit and emerge strategies and mathematical models.
Dig into our other units of study and view by concept continuum, grade or topic!