GRADUATION DAY
MULTIPLICATION
Sharpen estimation skills for two-digit by two-digit multiplication and connect tools and repesentations to begain thinking algebraically.
Intentionality
Spark Curiosity
Fuel Sensemaking
During Moves
Student Approaches
Next Moves
Consolidation
Reflect and Consolidation Prompts
Resources & Downloads
Educator Discussion Area
Intentionality & Unit Overview
Length of Unit: 2 Days
Access each lesson from this unit using the navigation links below
Students will determine how many chairs can fit in a gym for Grade 8 Graduation.
Intentionality…
As is true for any task, the intentionality or learning objective can vary depending on what mathematical thinking you are hoping to elicit. This task is a great way to help students solve problems using multiplication with concrete and/or visual models to make connections to symbolic algorithms.
Spark Curiosity
What Do You Notice? What Do You Wonder?
Show students this video:
Ask students to engage in a notice and wonder protocol. ANYTHING and EVERYTHING that comes to mind is fair game.
Here’s some of the “anything and everything” students noticed and wondered on chart paper:
- I notice the scene is a gymnasium.
- I notice basketball nets.
- I wonder why we’re looking at this video?
- I wonder if this is an elementary school or high school?
- And many others…
After taking student noticing and wondering, consider acknowledging and addressing any notices and wonderings that you can get “out of the way” at this point. For example, if a student says “what school is that?” you can say “John Campbell Public School in Windsor, Ontario.” etc.
Prompt and Estimate
The question we will land on for this task is:
How many chairs will fit in the gym for Grade 8 Graduation?
You can share the still image as well so students can try to use their spatial reasoning to make estimates, share and justify with their neighbours.
Fuel Sense-making
Crafting A Productive Struggle: Prompt
After students have shared estimates, show these images and prompt students to update their estimates given this newly revealed information.
Now, students are able to take the new information and update their estimates.
During Moves
While Students Are Productively Struggling…
Monitor student thinking by circulating around the room and listening to the mathematical discourse. Select and sequence some of the student strategies and ask a student from the selected groups to share with the class from:
- most accessible to least accessible solution strategies and representations;
- most common/frequent to least common/frequent strategies and representations; or,
- choose another approach to selecting and sequencing student work.
The key here is to get students to convince their neighbours of the number of chairs. Multiple representations are key and in particular, ensuring that all students are satisfied with “why” they came up with the number of chairs they did. The tools and representations you might see students using to convince their peers and/or the teacher include:
- Base ten blocks.
- Drawing area models.
- Student generated algorithms.
- Standard algorithms.
Have students share their strategies and reasoning for determining the number of cranks required to open the can.
Ask them to convince you and their peers that their answers are correct by sharing the mathematical models they used.
Discuss their strategies and elicit student thinking during your consolidation to build off of their current prior knowledge and understanding rather than “fixing” or “funnelling” student thinking to a strategy and/or model that does not connect to their strategy and/or approach.
Student Approaches
Sample Student Response #1:
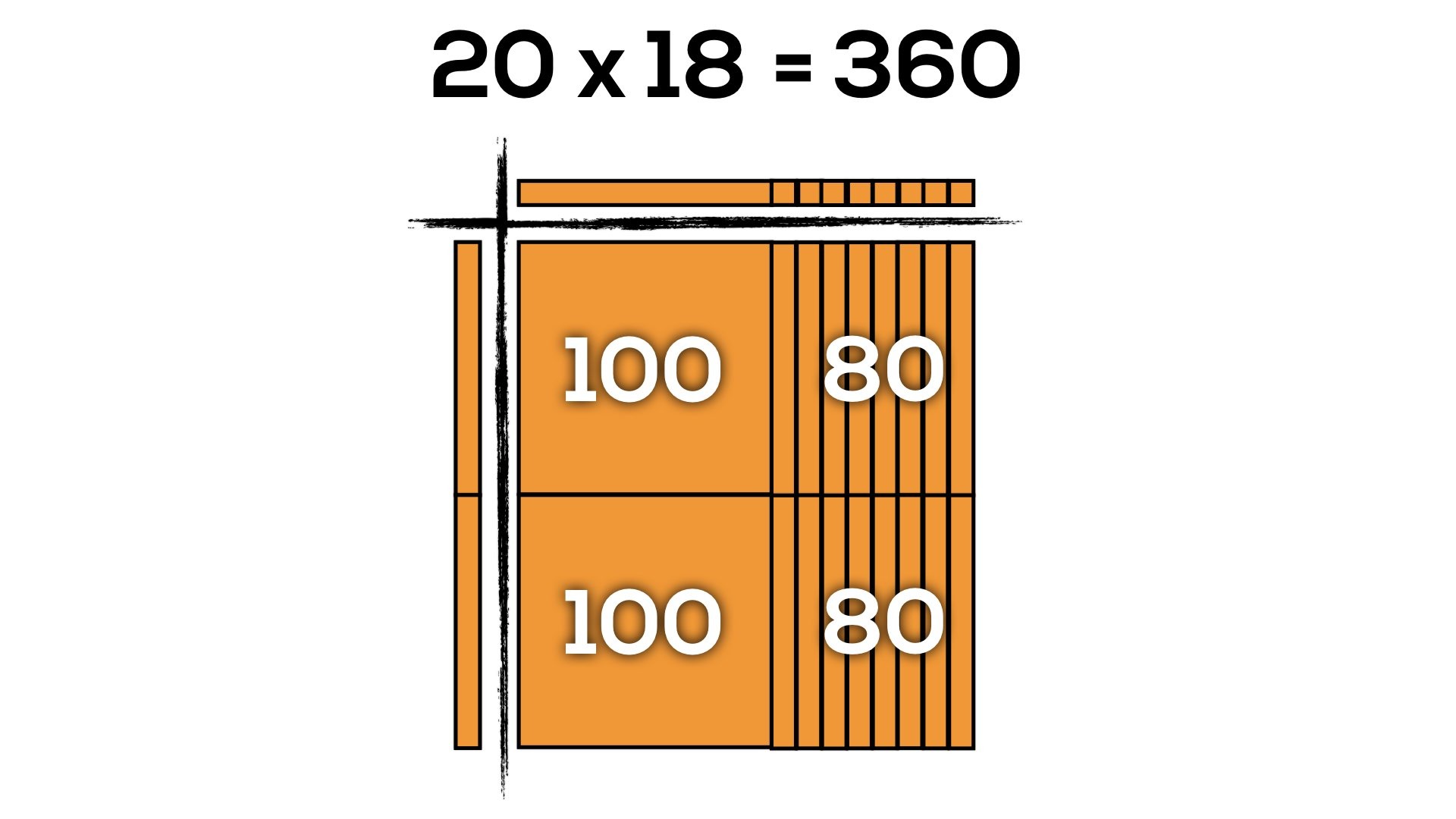
I took the dimensions of the gym in chairs of 18 by 20 and counted out a total of 360.
Sample Student Response #2:
I took the gym dimensions of 18 chairs by 20 chairs and created groups of 10. I showed my work using ten rods from the base ten block kit. When you count up all of the ten rods, I get 36 ten rods for 360 chairs total.
Sample Student Response #3:
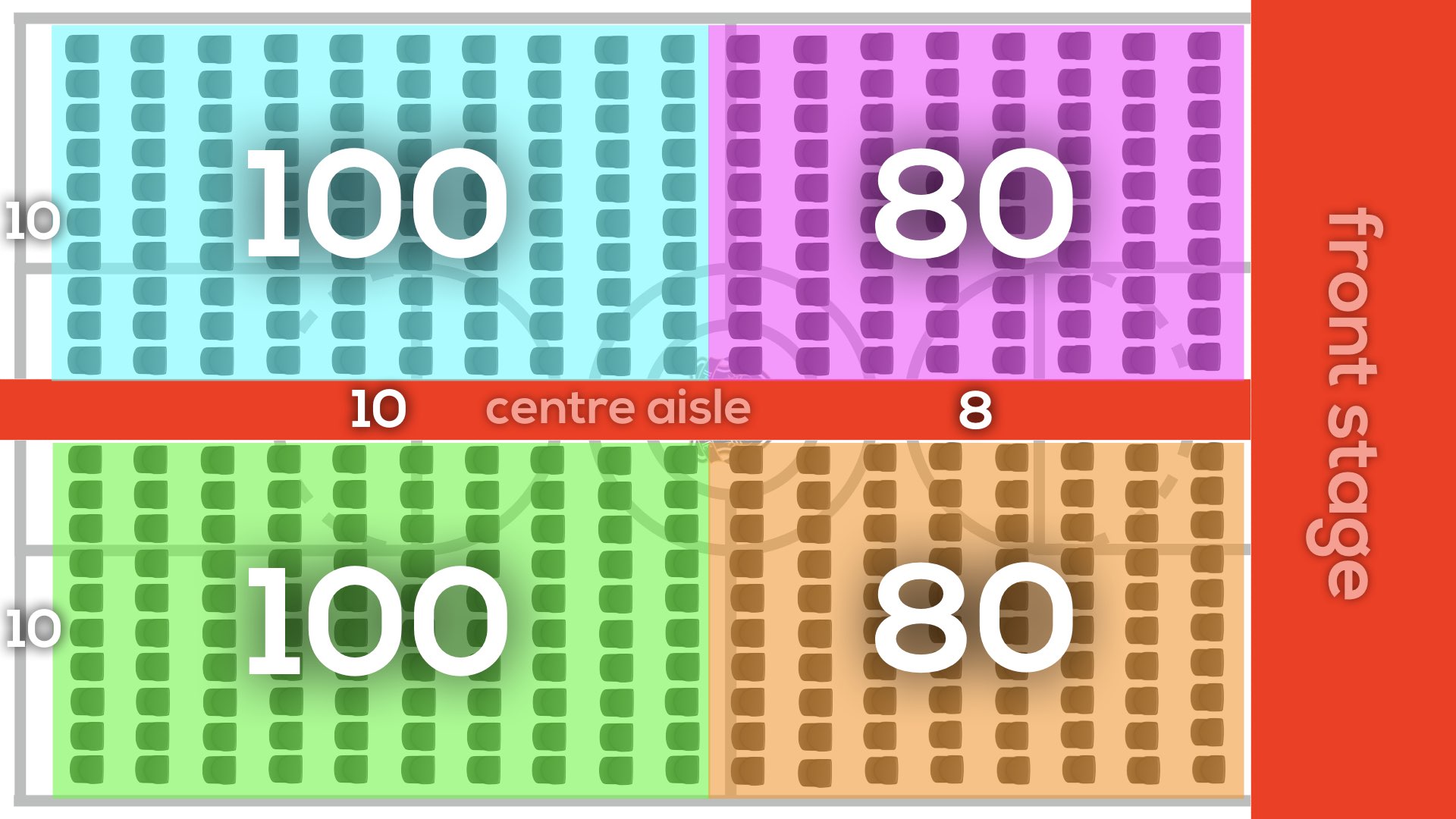
I created an array using base ten blocks with dimensions of 18 and 20 since the gym had 18 rows of 20 chairs.
Since I can break up 18 into 10 + 8 and 20 into 10 + 10, I could use 100 flats to take up big chunks of the array.
When I counted, I had 100 + 100 + 80 + 80 for a total of 360 chairs.
Sample Student Response #4:
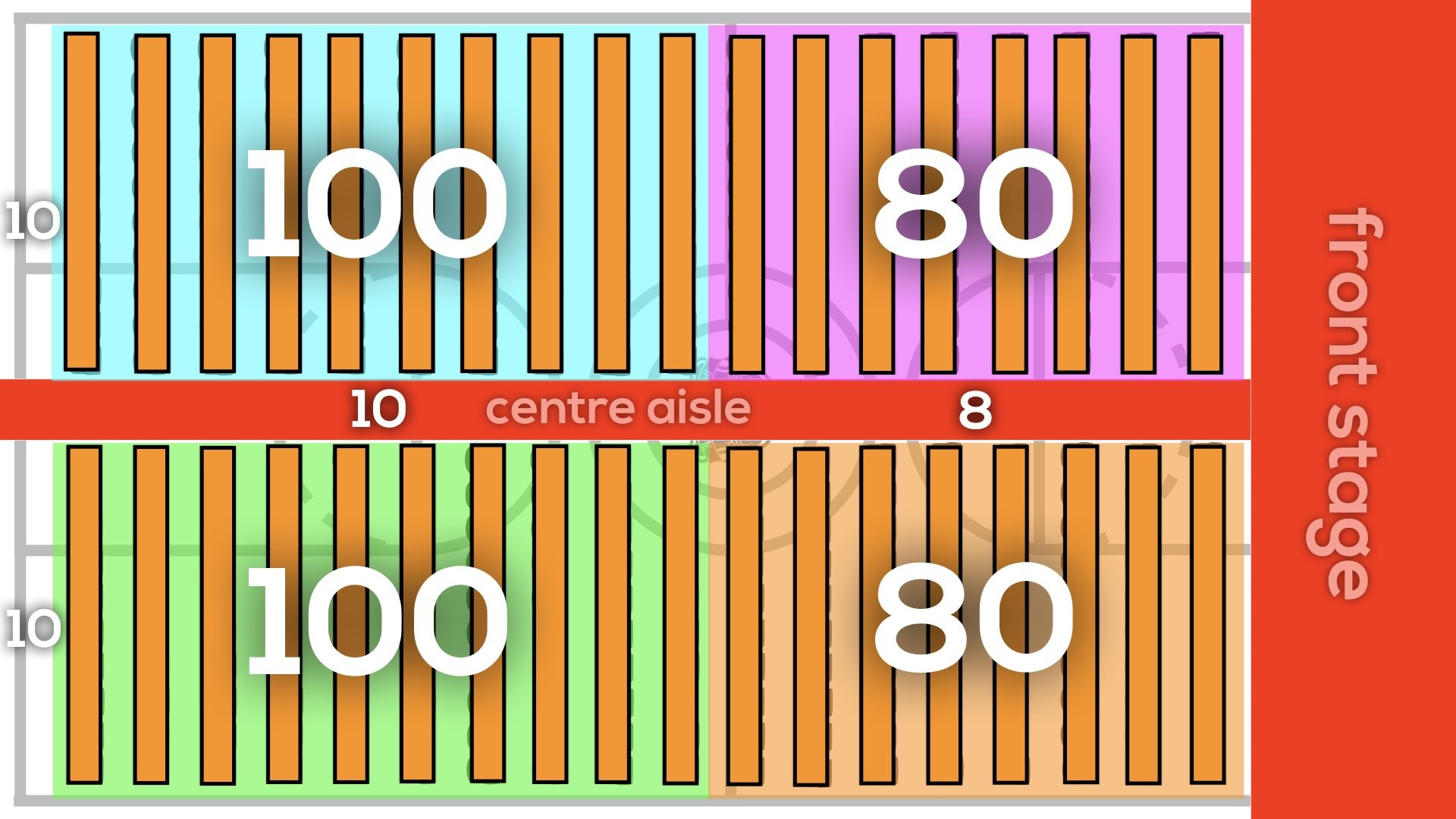
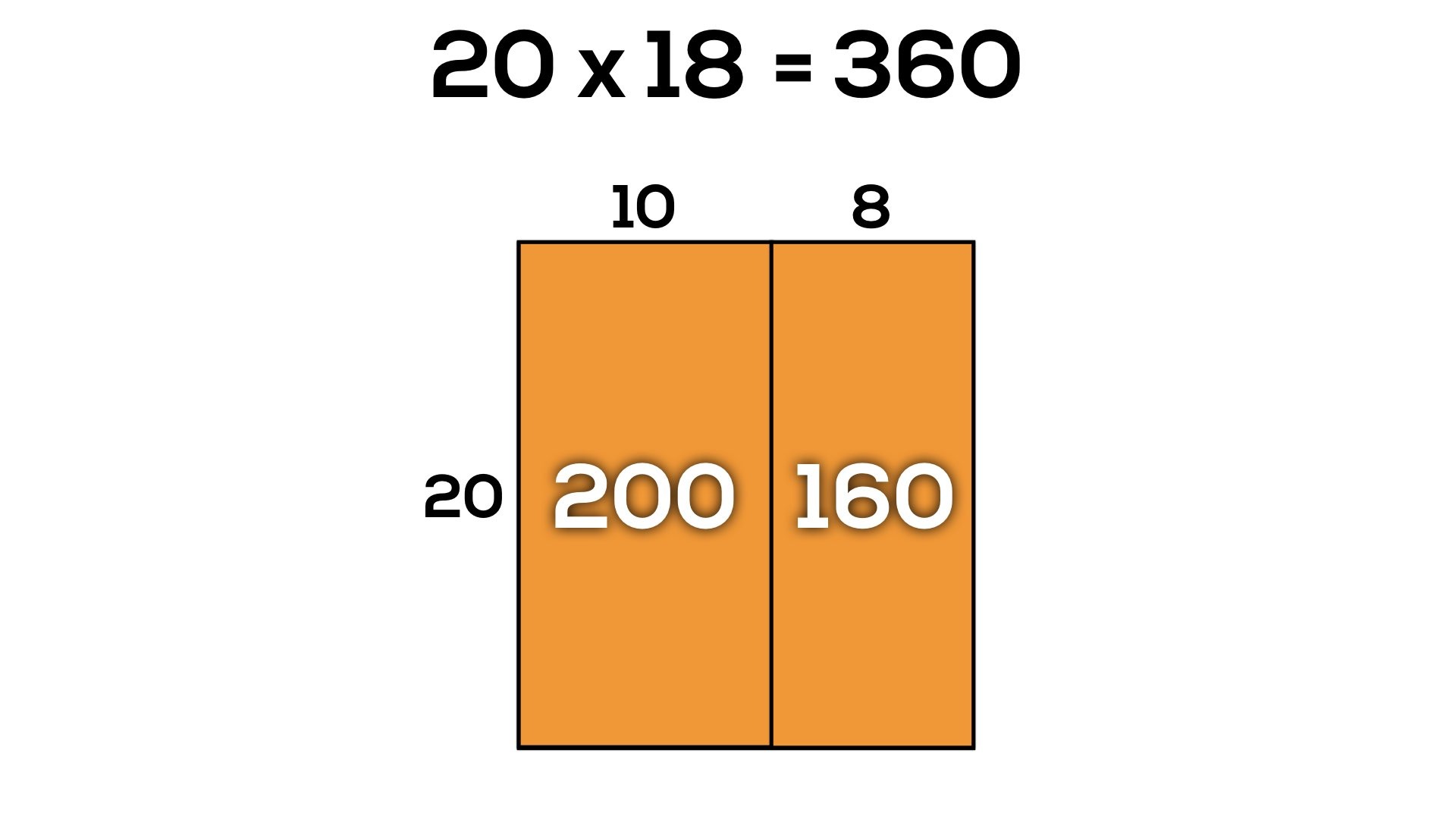
I created an area model to represent the gym with dimensions of 18 chairs and 20 chairs.
I know that multiplying 20 x 18 is easier if I use partial products by decomposing 18 into 10 + 8.
Since 20 x 10 = 200 and 20 x 8 = 160, I knew that there must be a total of 360 chairs.
Sample Student Response #5:
I used the standard algorithm by stacking 20 and 18:
20
x 18
0 (0 x 8)
160 (20 x 8)
0 (10 x 0)
+ 200 (10 x 20)
360
Next Moves
Reveal
After consolidating learning using student generated solution strategies and by extending their thinking intentionally, we can share what really happened with this video.
Or consider showing this image:
Students (and maybe even you as the facilitator) might be shocked when they see that the total number of seats is significantly less than the 360 seats they calculated.
Share the following prompt with students to discuss further:
The actual number of seats is different than the number of seats we expected.
How many rows and how many chairs in each row did they end up using for this graduation day ceremony?
Why do you suppose they changed their original plans?
Students might share that the guest list was smaller than originally anticipated or that they needed more leg/arm room between chairs/rows, etc.
After students discuss with neighbours, modify and/or create a new model to determine the factors that would result in 286 chairs, you can share the following image to confirm their findings:
Consolidation
The intent of monitoring students as they productively struggle through the task is to be able to provide more individualized purposeful questioning to nudge students along their learning journey as well as to select and sequence student generated solutions that can be leveraged during the consolidation.
Although there might be other solution strategies to leverage than what we will list here, keep in mind that trying to make too many connections can be overwhelming and thus limit the impact of the consolidation. A great opportunity for making connections during the consolidation could be selecting student samples that resemble:
- Student Solutions #1/2/3: Using Base Ten Blocks;
- Student Solution #4: Using an Area Model; and,
- Student Solution #5: Using the Standard Algorithm.
With these three (3) approaches, we can help students see that while the mathematical model used by each of the approaches is different, the strategy is very much connected. In particular, helping students to see both the concrete base ten model and area model inside of the standard algorithm can be helpful for them to understand that the algorithm is a proceduralized method to doing essentially the same work.
Another discussion point during consolidation could be to ask students to think about:
Which model shared (base ten, area model, standard algorithm) is most flexible to use when multiplying?
What we are hoping students can realize is that the area model is most flexible as we can use partial products in many different ways (distributive property) to “break up” the factors into as many managable chunks as we would like. Conversely, concrete base ten blocks and the standard algoirthm (in its current form) are “stuck” in base 10. In other words, the base ten blocks and the algorithm is already “chunked” for us leaving less flexibility to our thinking and strategy.
A perspective that might be surprising to many students who are using the standard algorithm and believe it to be “superior” to the other methods is that we might say the most valuable tool out of the three (3) would be the area model.
Consider showing an example using the area model such as breaking down the factors 18 x 20 into (9 + 9) x (10 + 10) showing a result of 90 + 90 + 90 + 90 = 360 as well as (10 + 5 + 3) x (10 + 10) showing another equivalent result of 100 + 100 + 50 + 50 + 30 + 30 = 360 using the area model to show these parts.
Reflect and Consolidation Prompts
Provide students an opportunity to reflect on their learning by offering these consolidation prompts to be completed independently.
Consolidation Prompt #1:
Which of the strategies and models shared during the consolidation did you find most useful to you? Why?
Give an example to show why you think the strategy and/or model you selected was more helpful to you than the others.
Consolidation Prompt #2:
A high school gym can fit 44 rows of 38 chairs for their graduation.
Without the use of a calculator, select an approach that you like using best.
Then, model it a second way using an approach that you aren’t as comfortable with.
Be sure that you show your thinking clearly enough that it would convince someone your answer is correct.
We suggest collecting this reflection as an additional opportunity to engage in the formative assessment process to inform next steps for individual students as well as how the whole class will proceed.
Resources & Downloads
Educator Discussion Area
Login/Join to access the entire Teacher Guide, downloadable slide decks and printable handouts for this lesson and all problem based units.
Explore Our 60+ Problem Based Units
This Make Math Moments Lesson was designed to spark curiosity for a multi-day unit of study with built in purposeful practice, number talks and extensions to elicit and emerge strategies and mathematical models.
Dig into our other units of study and view by concept continuum, grade or topic!
