GIRL GUIDE COOKIES
VOLUME OF RECTANGULAR PRISMS
Understand concepts of volume related to rectangular prisms.
Intentionality
Spark Curiosity
Fuel Sensemaking
During Moves
Student Approaches
Next Moves
Consolidation
Reflect and Consolidation Prompts
Resources & Downloads
Educator Discussion Area
Intentionality & Unit Overview

Length of Unit: 5 Days
Access each lesson from this unit using the navigation links below
Students will determine the volume of 8 boxes of Girl Guide cookies organized in a 2 x 2 x 2 rectangular prism. Students will measure the volume of the prism using cookies as their non-standard unit of measure.
Intentionality…
In this task, students will learn that one box of Girl Guide Cookies contains 24 cookies. They will observe 8 boxes being stacked together to form a rectangular prism (2 boxes x 2 boxes x 2 boxes). Students will be asked to draw the top and side view of the prism and to show the cookies that would be visible from both sides (if they had x-ray vision).
They will be asked to calculate the total number of cookies inside the rectangular prism, and to describe the dimensions of the rectangular prism using cookies as their unit of measure. This unit will support the development of the following big ideas:
- Volume and capacity can be measured using non-standard and standard units;
- A rectangular prism has three views. It can be viewed from the top, front and side. Each of these three faces are two dimensional, with a length and a width;
- A rectangular prism has three dimensions, which can be described using three linear measurements; the length, the width and the height;
- The measurements of length, width, and height are used to determine volume;
- Volume can be determined by multiplying the area of the base by the height of the prism;
- Volume is related to the operations of multiplication and addition;
- A solid figure which can be packed without gaps or overlaps using a quantity of unit cubes is said to have a volume of that same quantity of cubic units.
Spark Curiosity
What Do You Notice? What Do You Wonder?
Part 1
Show students the following video:
Then, ask students:
What do you notice?
What do you wonder?
Give students 60 seconds (or more) to do a rapid write on a piece of paper.
Replaying the video and/or leaving a screenshot from the video up can be helpful here.
Then, ask students to share with their neighbours for another 60 seconds.
Finally, allow students to share with the entire group. Be sure to write down these noticings and wonderings on the blackboard/whiteboard, chart paper, or some other means to ensure students know that their voice is acknowledged and appreciated.
Some of the noticing and wondering that may come up includes:
- I notice a box.
- I notice the name is Sweet Shop.
- I notice cookies.
- I notice 2 rows of cookies.
- It looks like about 8 cookies are showing.
- I wonder how many cookies there are in the whole box?
- I wonder what kinds of cookies they are?
- I wonder if they are Girl Guide Cookies?
At this point, you can answer any wonders that you can cross off the list right away. For example:
- This is one box of cookies that are being sold for a school fundraiser.
- They are shortbread cookies.
You might consider adding other details that you feel will be helpful to build an understanding of the context.
Part 2
Show students the following video:
Then, ask students:
What do you notice?
What do you wonder?
Give students 60 seconds (or more) to do a rapid write on a piece of paper.
Replaying the video and/or leaving a screenshot from the video up can be helpful here.
Then, ask students to share with their neighbours for another 60 seconds.
Finally, allow students to share with the entire group. Be sure to write down these noticings and wonderings on the blackboard/whiteboard, chart paper, or some other means to ensure students know that their voice is acknowledged and appreciated.
Some of the noticing and wondering that may come up includes:
- I notice there are eight boxes.
- I notice the eight boxes make one big rectangle.
- I wonder how many cookies there are.
- I wonder if all of the boxes are full.
- I wonder if it is the same type of cookie.
At this point, you can answer any wonders that you can cross off the list right away. For example:
- These are the same boxes of Shortbread Cookies.
- There are 8 boxes.
Estimation: Prompt
After we have heard students and demonstrated that we value their voice, we can land on the first questions we will challenge them with:
If you could look down on this arrangement of boxes from above with x-ray vision, how many cookies do you think you would see on the top layer? Draw a diagram of how the cookies would be arranged.
We can now ask students to draw a diagram of the cookies viewed from the top of this arrangement of boxes. Encourage them to actually identify the cookies pictorially or concretely and represent how they would be arranged in their columns and rows. Encourage students to engage in a conversation about how many cookies they would see from the top of the boxes, and how they know.
Estimation: Partial Reveal
Share the following image:
![Girl Guide Cookies [Day 1] - 06 - Spark Estimate Partial Reveal Image.001](https://learn.makemathmoments.com/wp-content/uploads/2021/06/Girl-Guide-Cookies-Day-1-06-Spark-Estimate-Partial-Reveal-Image.001.jpeg)
Engage students in a conversation around the dimensions and the total area of the top view using cookies as your unit of measure.
Fuel Sense-making
Crafting A Productive Struggle: Prompt
Prompt students with the following:
Prompt #1:
Draw a diagram of the side view of this arrangement.
Make sure that your diagrams show how the first layer of cookies would be organized in their rows and columns if you could see through the boxes with your x-ray vision.
After giving students some time to estimate how many layers are in each box, you can prompt them with the following:
Prompt #2:
How many cookies are in this arrangement of boxes altogether? How do you know?
Students should reason through this prompt without the use of a calculator. Visual or concrete representations are expected of all learners.
During Moves
While Students Are Productively Struggling…
Monitor student thinking by circulating around the room and listening to the mathematical discourse. Select and sequence some of the student solution strategies and ask a student from the selected groups to share with the class from:
- most accessible to least accessible solution strategies and representations;
- most common/frequent to least common/frequent strategies and representations; or,
- choose another approach to selecting and sequencing student work.
The tools and representations you might see students using to convince their peers and/or the teacher include:
- Using linking cubes.
- Using a pictorial representation with circles for each cookie.
- Using an array.
- Using a formula or numeric representation.
- Using addition.
- Using skip-counting.
- Using multiplication.
Have students share their strategies and reasoning for how to draw their diagrams and determine the total number of cookies. Ask them to convince you and their peers that their answer is correct by sharing their mathematical models.
Discuss their strategies and elicit student thinking during your consolidation to build off of their current prior knowledge and understanding rather than “fixing” or “funnelling” student thinking to a strategy and/or model that does not connect to their strategy and/or approach.
Student Approaches
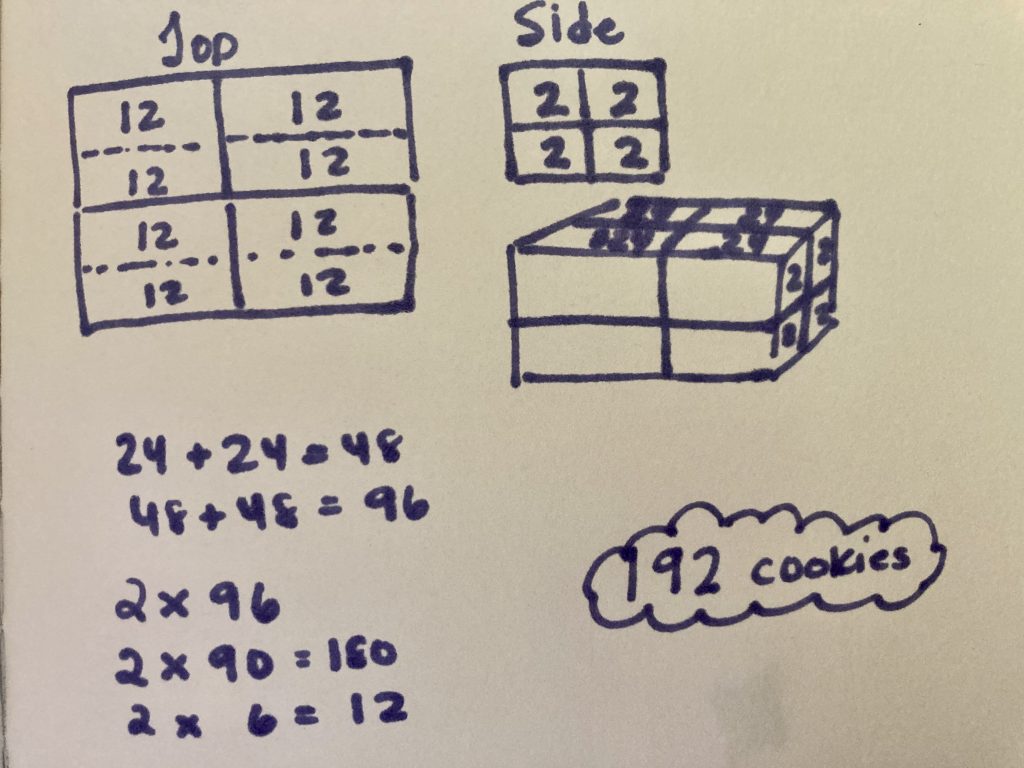
Student Approach #1: Linking Cubes with Addition Using Compensation
I started by building the top row of boxes. I know there are four boxes on the top, and there are two rows of 12 cookies in each box. From the side, I know that I will have that row of boxes, with another row underneath. From the side I will see two rows of four cookies. If there are 96 cookies on the top row, there are 96 cookies on the bottom. 96 + 96 is the same as 100 + 100, – 8. So there are 192 cookies.
Student Approach #2: Pictorial Representation with Addition Using Partial Sums
I drew four boxes from the top, each box has two rows of 12 cookies, so each box has 24 cookies. From the side, I can see four boxes, and each box has two rows of cookies. Because there are eight boxes altogether, there are actually two rows of 4 boxes stacked on top of each other. If the top row has 96 cookies, then 96 + 96 = 192 cookies altogether.
Student Approach #3: Open Array with Multiplication Using Partial Products
I have four boxes on top. Each box has two rows of 12 cookies. So the dimensions of the top are 4 cookies by 24 cookies. From the side, I would see two boxes side by side, and another row of two boxes side by side underneath. The dimensions are 2 cookies by 2 cookies. 2 x 96 is the same as (2 x 90) + (2×6)
Next Moves
Consolidation
Through today’s consolidation, we really want to begin emerging the relationship between the area of the base, and the height of the prism.
It is important in the early development of the concept of volume for students to be able to visualize the layers of units within the prism, which is why this first task measures the volume in cookies, because they are concrete and tangible.
As students move into more abstract units of measure, they should still be able to visualize the units layered within the prism with no gaps or overlaps, completely filling the space.
During the consolidation, draw connections to how students went about determining the total number of cookies, did they skip count, add or multiply? Highlight the connection between addition and multiplication to the concept of volume.
Reflect and Consolidation Prompts
Provide students an opportunity to reflect on their learning by offering this consolidation prompt to be completed independently.
Consolidation Prompt:
18 boxes of chocolate are placed in a larger box for shipment.
- Draw a diagram highlighting how the boxes of chocolates might have been organized in the larger box for shipment. Label the dimensions of your larger box using individual chocolates as the unit of measure.
- How many chocolates are in a single layer of your box?
- How many chocolates are there altogether?
Be sure to convince the reader of your thinking.
We suggest collecting this reflection as an additional opportunity to engage in the formative assessment process to inform next steps for individual students as well as how the whole class will proceed.
Resources & Downloads
Printable Lesson Plan PDF
Videos, Images & Media Files
Apple Keynote Presentation
Powerpoint Presentation
Printable Consolidation Prompts
Educator Discussion Area
Login/Join to access the entire Teacher Guide, downloadable slide decks and printable handouts for this lesson and all problem based units.
Explore Our 60+ Problem Based Units
This Make Math Moments Lesson was designed to spark curiosity for a multi-day unit of study with built in purposeful practice, number talks and extensions to elicit and emerge strategies and mathematical models.
Dig into our other units of study and view by concept continuum, grade or topic!


![Girl Guide Cookies [Day 1] - 02 - Spark Image.001](https://learn.makemathmoments.com/wp-content/uploads/2021/06/Girl-Guide-Cookies-Day-1-02-Spark-Image.001.jpeg)
![Girl Guide Cookies [Day 1] - 04 - Spark Notice Wonder Part 2 Image.001](https://learn.makemathmoments.com/wp-content/uploads/2021/06/Girl-Guide-Cookies-Day-1-04-Spark-Notice-Wonder-Part-2-Image.001.jpeg)
![Girl Guide Cookies [Day 1] - 05 - Spark Estimate Prompt Image.001](https://learn.makemathmoments.com/wp-content/uploads/2021/06/Girl-Guide-Cookies-Day-1-05-Spark-Estimate-Prompt-Image.001.jpeg)
![Girl Guide Cookies [Day 1] - 07 - Sense Making - Prompt 1 Image - Side View Arrangement.001](https://learn.makemathmoments.com/wp-content/uploads/2021/06/Girl-Guide-Cookies-Day-1-07-Sense-Making-Prompt-1-Image-Side-View-Arrangement.001.jpeg)
![Girl Guide Cookies [Day 1] - 08 - Sense Making - Prompt 2 Image - How Many Cookies.001](https://learn.makemathmoments.com/wp-content/uploads/2021/06/Girl-Guide-Cookies-Day-1-08-Sense-Making-Prompt-2-Image-How-Many-Cookies.001.jpeg)


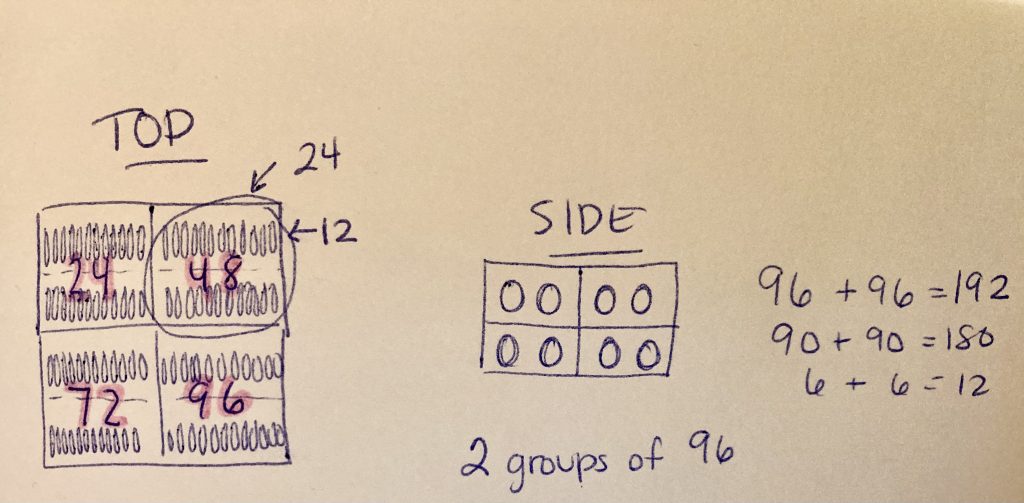
![Girl Guide Cookies [Day 1] - 10 - After Moves - Reveal Image.001](https://learn.makemathmoments.com/wp-content/uploads/2021/06/Girl-Guide-Cookies-Day-1-10-After-Moves-Reveal-Image.001.jpeg)
![Girl Guide Cookies [Day 1] - 11 - After Moves - Reflect Consolidation Prompt Image.001](https://learn.makemathmoments.com/wp-content/uploads/2021/06/Girl-Guide-Cookies-Day-1-11-After-Moves-Reflect-Consolidation-Prompt-Image.001.jpeg)

