COVERING GROUND
AREA OF A TRIANGLE & PARALLELOGRAM
Investigate the area of a triangle and area of a parallelogram to generalize a formula for each.
Intentionality
Spark Curiosity
Fuel Sensemaking
During Moves
Student Approaches
Next Moves
Consolidation
Reflect and Consolidation Prompts
Resources & Downloads
Educator Discussion Area
Intentionality & Unit Overview

Length of Unit: 5 Days
Access each lesson from this unit using the navigation links below
Students will leverage the relationship between triangles and rectangles to uncover the formula for calculating the area of a triangle.
In this task, students will explore the relationship between rectangles and triangles. They will use their prior knowledge of the area of a rectangle to uncover the formula for calculating the area of a triangle. Some of the big ideas that may emerge in this unit include:
- The area of a rectangle can be determined by multiplying the length of its base by the length of its height;
- The area of a rectangle is used to determine the area formulas for other polygons;
- Using “base” and “height” rather than “length” and “width” can support student understanding when determining the area formulas for triangles and all quadrilaterals;
- A parallelogram is any quadrilateral with two sets of parallel sides;
- A rectangle is a parallelogram;
- Any triangle can be doubled to create a parallelogram; and,
- Congruent shapes have the same size and shape, but not necessarily the same orientation.
Spark Curiosity
What Do You Notice? What Do You Wonder?
Show students this video:
The video shows a square backyard with dirt and sod (pre-cut pieces of grass to use for a lawn) being “rolled out” to cover the backyard area. However, this might not be initially obvious to students.
Then, ask students:
What do you notice?
What do you wonder?
Give students 60 seconds (or more) to do a rapid write on a piece of paper.
Then, ask students to share with their neighbours for another 60 seconds.
Finally, allow students to share with the entire group.
Some of the noticing and wondering that came up in a class recently included:
- I notice a square.
- I notice small green squares being placed.
- I wonder if this is a yard.
- I wonder if the green is grass.
- I wonder how many pieces of grass are placed in the yard.
At this point, you can answer any notices and wonders that you can cross off the list right away.
For example:
- This is a backyard.
- The backyard is being covered in sod.
- Sod is pre-cut sections of grass that is used to cover a yard quickly instead of planting grass seed and having to wait for it to grow.
Estimation: Prompt
Next, share the following visual prompt briefly and ask the following question:
Each piece of sod (grass) placed on the ground in the backyard measures 1 square metre. Estimate how many square metres will cover the entire area of this backyard?
We can now ask students to make an estimate (not a guess) as we want them to be as strategic as they can possibly be. This will force them to use reasoning to try and come up with a reasonable measurement.
As students share their estimates, consider drawing a number line to represent the range of estimates and lead a discussion about how confident the group is that the actual number of pieces of sod will land within the range.
While Students Are Estimating…
Monitor student thinking by circulating around the room and listening to the mathematical discourse. Encourage students to use precise mathematical language and listen for student understanding of how to determine the area of a rectangle. Are students using the dimensions of the square to determine the total number of square units?
Allow students to share their estimates with neighbours first, then with the class. Write down their estimates on the chalkboard/whiteboard/chart paper so students feel their voices are being heard and so they feel they have a stake in solving this problem.
Estimation: Update
You might offer students a visual that shows the lawn partitioned into 1 square-metre sections of sod and then ask them to:
Update your estimate.
Monitor how students update their estimates. Do their approaches change? Record their updated estimates on the number line. Be sure to note the change in the range of estimates. Is the range tighter now?
Estimation: Reveal
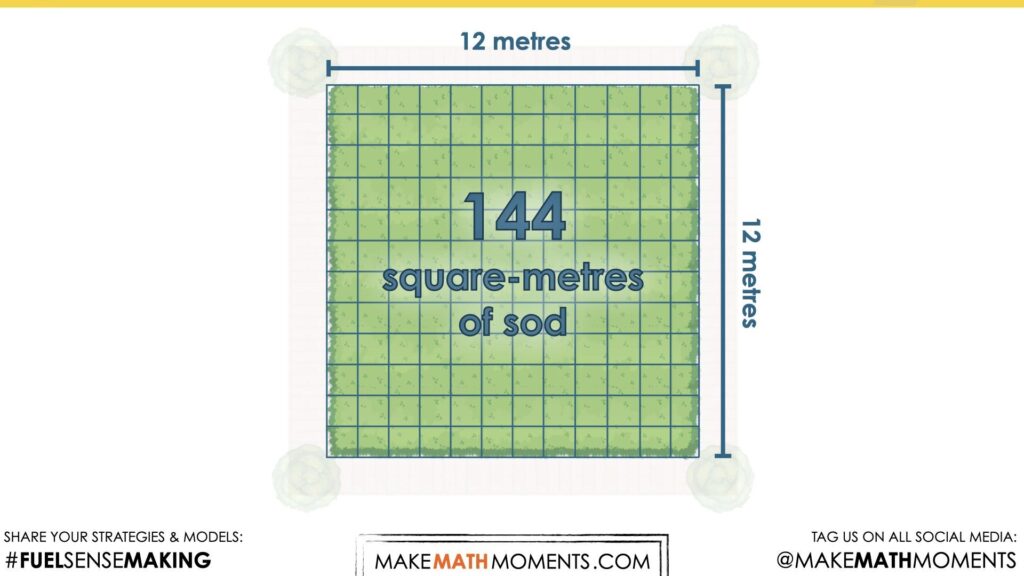
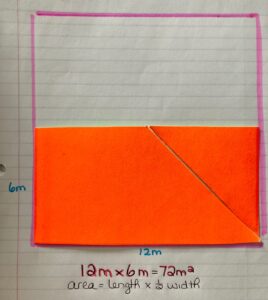
Share the following image revealing that the yard is 12 metres by 12 metres long, which gives 144 square-metres of area to cover with sod.
Fuel Sense-making
Crafting A Productive Struggle: Prompt
Since you have already taken some time to set the context for this problem and student curiosity is already sparked, we have them in a perfect spot to help push their thinking further and fuel sense making.
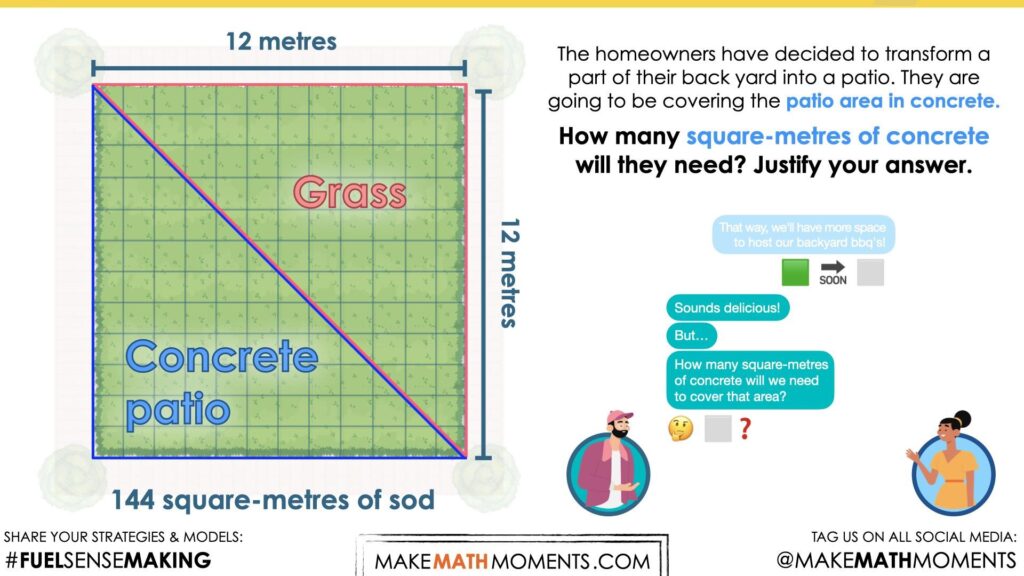
Share the following silent animation that shows the same 12 metre by 12 metre backyard being split diagonally to have a triangular section of sodded grass area and a triangular section of concrete patio.
You can verbally share the following prompt with students:
The homeowners have decided to transform a part of their back yard into a patio. They are going to be covering the patio area in concrete. How many square metres of concrete will they need? Justify your answer.
During Moves
While Students Are Productively Struggling…
Monitor student thinking by circulating around the room and listening to the mathematical discourse. Select and sequence some of the student solution strategies and ask a student from the selected groups to share with the class from:
- most accessible to least accessible solution strategies and representations;
- most common misconceptions;
- most common/frequent to least common/frequent representations; or,
- choose another approach to selecting and sequencing student work.
The strategies you might see students use include:
- Counting the square pieces of sod in one half of the yard;
- Halving the total area of the rectangle;
- Using a formula to calculate the area of the triangular section.
Have students share their reasoning for determining the area of concrete in square metres.
Discuss their thinking during your consolidation to build off of their current prior knowledge and understanding rather than “fixing” or “funnelling” student thinking to a representation and justification that does not connect to their understanding.
Student Approaches
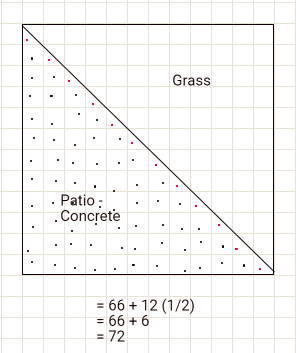
Student Approach #1: Counting the Whole & Half Squares
To find out how many square metres of concrete are needed, I counted all the full pieces of sod, and then all the half pieces of sod. I added them together. I can see that 72 square metres are needed to cover the patio.
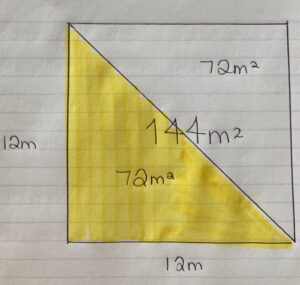
Student Approach #2: Halving the Total Area
I think that when they split the yard diagonally, they cut it in half. I think the patio and the grass are the same size. So if the total area of the backyard is 144 metres squared, then half is 72 metres squared. I checked my prediction by making a square, cutting it in half diagonally and then confirming that the two triangles are the same size.
Student Approach #3: Decomposing and Recomposing
It looked to me that cutting the yard diagonally into two triangles was the same as cutting it in half. To be completely sure, I cut out a square and traced it on my page. Then I cut the square diagonally, just like in the video. To check that the triangle is half the yard, I cut the triangle and rearranged it to fit in half the square. So basically, the area is the same length as the rectangle, but half the height. The area is 72 metres squared.
Student Approach #4: Area of a Triangle Formula
Last year, my teacher taught us the formula for the area of a triangle. It was:
A = (\(\frac{1}{2}\))bh
Since the base of the triangle is 12 metres and the height of the triangle is 12 metres, then I need to take half of 12 metres x 12 metres or half of 144 square-metres. The area of the concrete patio is 72 metres squared.
Next Moves
Reveal
Show students the following reveal video that partitions the yard diagonally into two triangles that each cover half of the yard. One of the triangles will flip to “cover” the other triangle to make it clear that each triangle represents half of the square (rectangular) yard.
You can consider sharing the screenshot of the final frame of the video as well.
Consolidation
The big idea in today’s consolidation is to examine the relationship between the area of a rectangle, and the area of a triangle.
In today’s context, students likely realized that the patio area of the yard is half the total backyard area.
Conclusions that we can make from this observation:
- A rectangle (or any other parallelogram) can be decomposed into two congruent triangles.
- Any triangle can be doubled to make a parallelogram (a rectangle is a parallelogram).
Based on the findings, what can we say about the area of a triangle?
Help students land on the formula through investigation and confirmation of these big ideas. You may want to test these generalizations with other rectangles (or any other parallelograms) and congruent triangles. It is helpful when students actually take construction paper and cut them out in order to compose and decompose. They will likely want to investigate triangles that are not right angles.
Some version of the standard formula will likely emerge as students confirm this understanding.
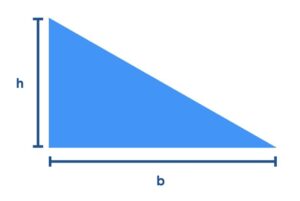
area of a triangle = (base x height) ÷ 2
or
area of a triangle = \(\frac{1}{2}\)bh
Although students may be familiar with length times width as the formula for the area of a rectangle, we are going to nudge students towards base x height. This shift will be helpful as we continue exploring the areas of other polygons.
Consider sharing the following consolidation video to reiterate the various ways rectangles can be partitioned in half to create triangles (and visa versa).
Reflect and Consolidation Prompts
Provide students an opportunity to reflect on their learning by offering these consolidation prompts to be completed independently.
Consolidation Prompt #1:
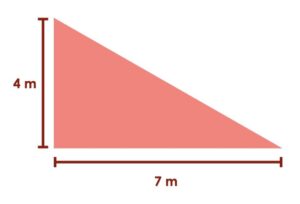
What is the area of the triangle below? Justify your answer.
Consolidation Prompt #2:
The area of a triangle is half the area of a rectangle with the same length base and height. Defend this statement.
Consolidation Prompt #3:
The cost of sod is $6.75 per square-metre, while the cost to hire a company to cement a patio is $180 per square-metre.
- How much will it cost to sod the 72 square-metre section of grass and cement the 72 square-metre section of patio? Do not consider any taxes or additional charges.
- In some states or provinces, the government charges a sales tax calculated as a percentage of the total cost. What would the sales tax be for areas that have a:
- 10% sales tax?
- 5% sales tax?
- 15% sales tax?
- What is the sales tax in your region? Use it to calculate the sales tax on the cost of the sod and cement patio.
We suggest collecting this reflection as an additional opportunity to engage in the formative assessment process to inform next steps for individual students as well as how the whole class will proceed.
Resources & Downloads
Printable Lesson Plan PDF
Videos, Images & Media Files
Apple Keynote Presentation
Powerpoint Presentation
Printable Consolidation Prompts
Educator Discussion Area
Login/Join to access the entire Teacher Guide, downloadable slide decks and printable handouts for this lesson and all problem based units.
Explore Our 60+ Problem Based Units
This Make Math Moments Lesson was designed to spark curiosity for a multi-day unit of study with built in purposeful practice, number talks and extensions to elicit and emerge strategies and mathematical models.
Dig into our other units of study and view by concept continuum, grade or topic!