COVERING GROUND [DAY 4]
AREA OF A TRIANGLE & PARALLELOGRAM
Investigate the area of a triangle and area of a parallelogram to generalize a formula for each.
Intentionality
Math Talk
Visual Math Talk Prompt #1
Visual Math Talk Prompt #2
Visual Math Talk Prompt #3
Visual Math Talk Prompt #4
Purposeful Practice
Resources & Downloads
Educator Discussion Area
Intentionality & Unit Overview

Length of Unit: 5 Days
Access each lesson from this unit using the navigation links below
Students will continue exploring how to determine the area of any parallelogram when the base and height is known.
Intentionality…
The purpose of the Day 4 activities is to reinforce key concepts from Day 3. Students will engage in a math talk and will have an opportunity to complete independent purposeful practice. The math talk and purposeful practice serve to develop a deeper understanding of the following big ideas.
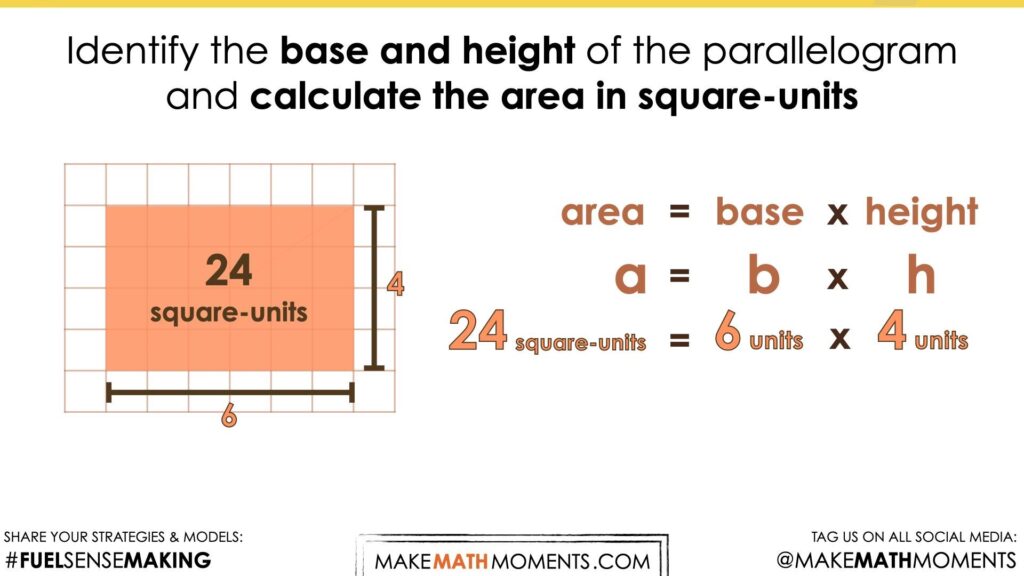
- The area of a rectangle can be determined by multiplying the length of its base by the length of its height;
- The area of a rectangle is used to determine the area formulas for other polygons;
- Using “base” and “height” rather than “length” and “width” can support student understanding when determining the area formulas for triangles and all quadrilaterals;
- A parallelogram is any quadrilateral with two sets of parallel sides;
- A rectangle is a parallelogram;
- Any triangle can be doubled to create a parallelogram;
- Congruent shapes have the same size and shape, but not necessarily the same orientation;
- Any parallelogram can be decomposed and recomposed to build a rectangle with the same area.
Math Talk
Present the following parallelograms one at a time. Students are asked to identify the base and the height of each parallelogram, and then calculate the area in square units. Encourage students to share their thinking as you model their strategies symbolically.
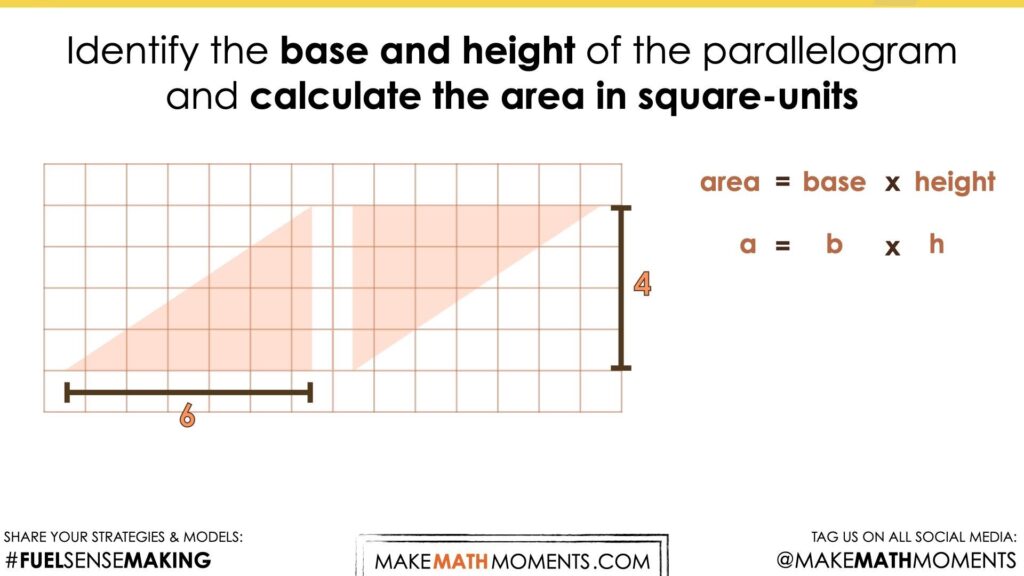
Model how each of the following parallelograms can be decomposed and recomposed to create a rectangle with the same area if that is not obvious to students.
Parallelogram #1 : 3 x 4
Parallelogram #2: 6 x 4
Parallelogram #3: 6 x 8
Parallelogram #4: 12 x 8
Providing students with grid paper could be helpful for them to draw, decompose and recompose each parallelogram into rectangles to determine the area.
The following set of visual number talk prompt videos are provided to ensure that all students can see visually why the area of a parallelogram is equivalent to the area of a rectangle with the same base and height.
Facilitator note:
There is a relationship between these parallelograms. From the first to the second, the length of the base is doubled. From the first to the third, both the base and the height are doubled. From the third to the fourt, the base is again doubled. Ask students to make generalisations about the result of doubling one dimension, versus doubling both the base and the height.
For example:
- When you double one dimension, the area is doubled.
- When you double both dimensions, the area is quadrupled.
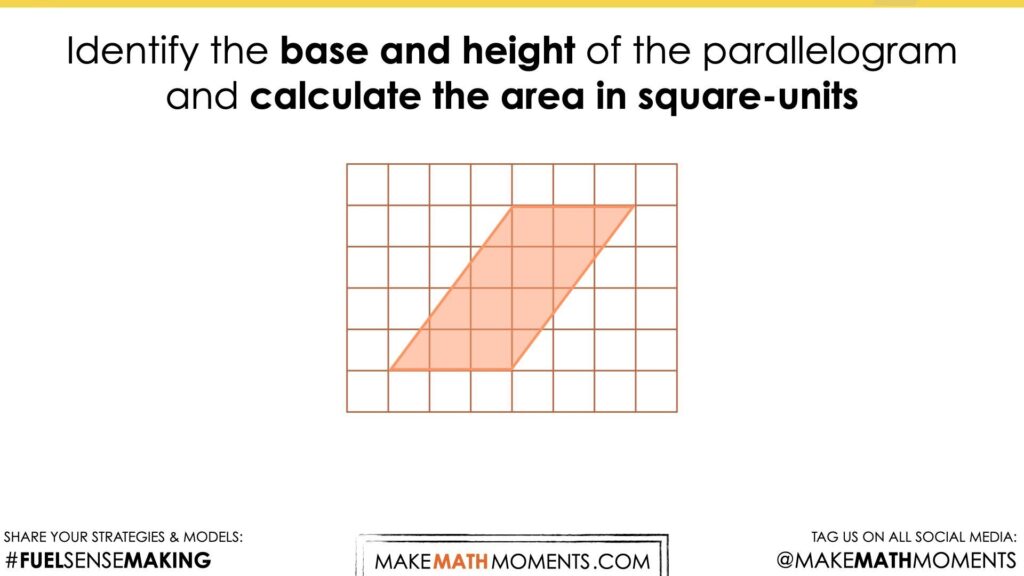
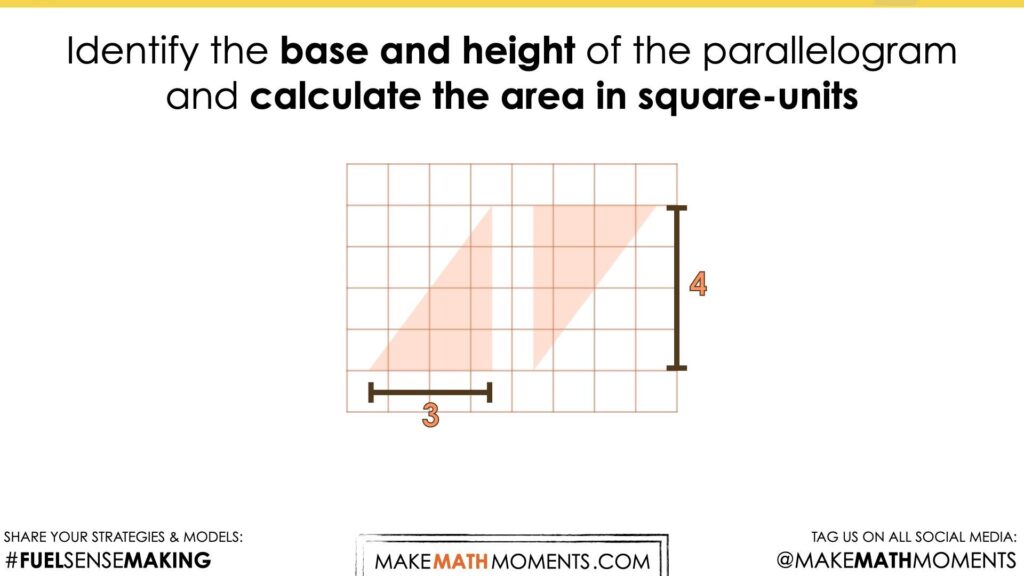
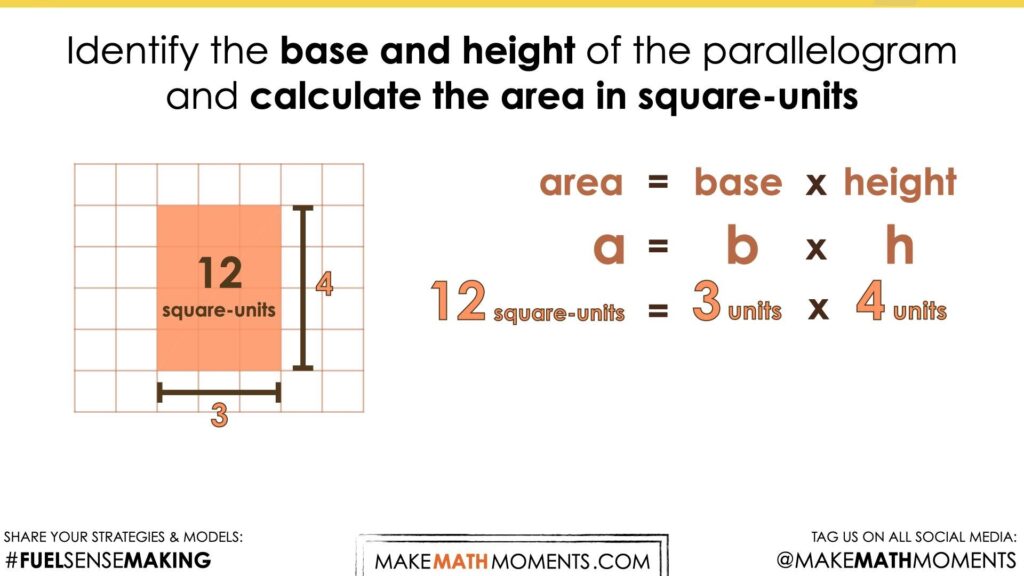
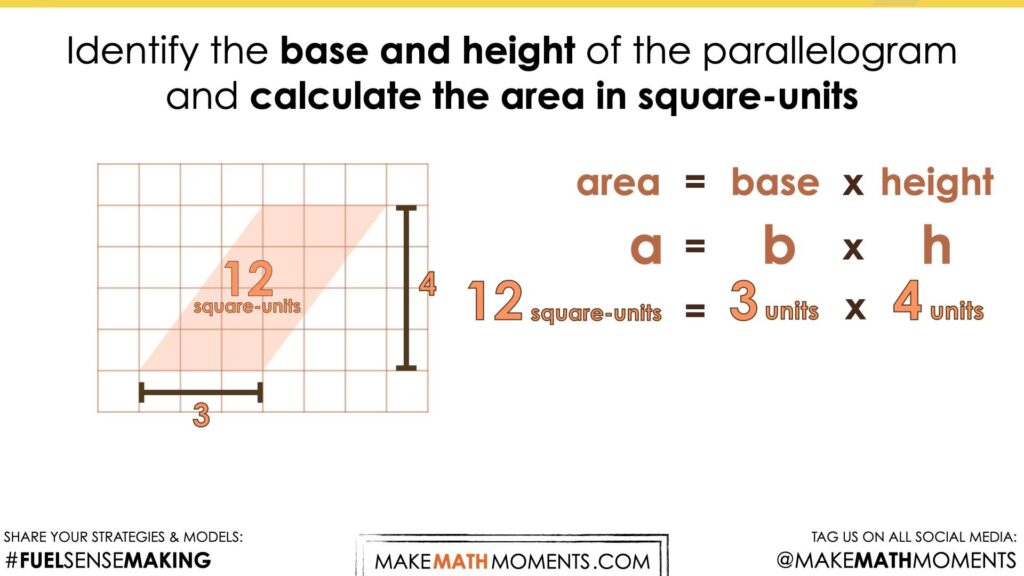
Visual Math Talk Prompt #1
Begin playing the following visual number talk prompt video and be ready to pause the video to allow for think time.
After a grid and a parallelogram appear on the screen, pause the video and share the following prompt:
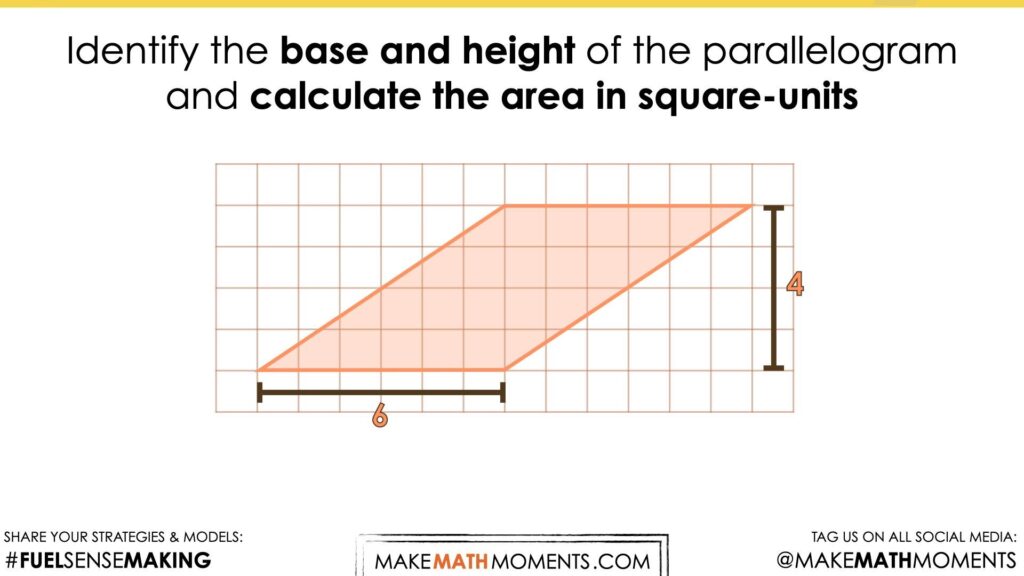
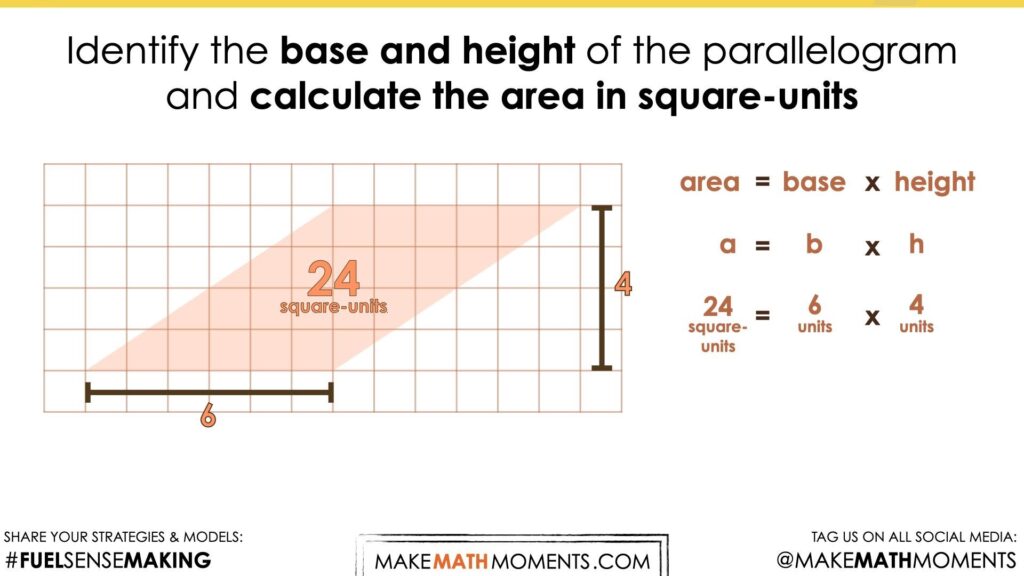
Identify the base and height of the parallelogram and calculate the area in square-units.
As we explore these visual prompts, we want students to begin visualizing the decomposition of each parallelogram and recomposition into a rectangle to drive home the connection between the area of a parallelogram and the area of a rectangle.
As students engage in this work, they will be able to quickly identify the base and height of a parallelogram and visualize both measures as the length and width of a rectangle with an equivalent area.
Repeatedly finding the area of a rectangle and seeing this quantity of square units as equivalent to the area covered by a parallelogram with the same dimensions is important to strengthen the conceptual understanding of students and allow them to work towards building procedural fluency.
Visual Math Talk Prompt #2
Begin playing the following visual number talk prompt video and be ready to pause the video to allow for think time.
After a grid and a parallelogram appear on the screen, pause the video and share the following prompt:
Identify the base and height of the parallelogram and calculate the area in square-units.
Again, encourage students to visualize the parallelogram being decomposed and recomposed into a rectangle with a length of 6 units and a width of 4 units.
From this, students will be able to quickly identify the area of both the rectangle and the area of the parallelogram.
If students are still not writing down their thinking symbolically, encourage this activity to ensure that they build a connection between the visual and the symbolic representations.
Visual Math Talk Prompt #3
Login/Join to access the entire Teacher Guide, downloadable slide decks and printable handouts for this lesson and all problem based units.
Visual Math Talk Prompt #4
Login/Join to access the entire Teacher Guide, downloadable slide decks and printable handouts for this lesson and all problem based units.
Purposeful Practice
Login/Join to access the entire Teacher Guide, downloadable slide decks and printable handouts for this lesson and all problem based units.
Questions: Area of a Parallelogram
Login/Join to access one (1) additional Math Talk Prompt as well as the Teacher Guide, downloadable slide decks and printable handouts for this lesson and all problem-based units.
Resources & Downloads
Login/Join to access the entire Teacher Guide, downloadable slide decks and printable handouts for this lesson and all problem based units.
Printable Lesson Plan PDF
Videos, Images & Media Files
Apple Keynote Presentation
Powerpoint Presentation
Printable Consolidation Prompts
Educator Discussion Area
Login/Join to access the entire Teacher Guide, downloadable slide decks and printable handouts for this lesson and all problem based units.
Explore Our 60+ Problem Based Units
This Make Math Moments Lesson was designed to spark curiosity for a multi-day unit of study with built in purposeful practice, number talks and extensions to elicit and emerge strategies and mathematical models.
Dig into our other units of study and view by concept continuum, grade or topic!