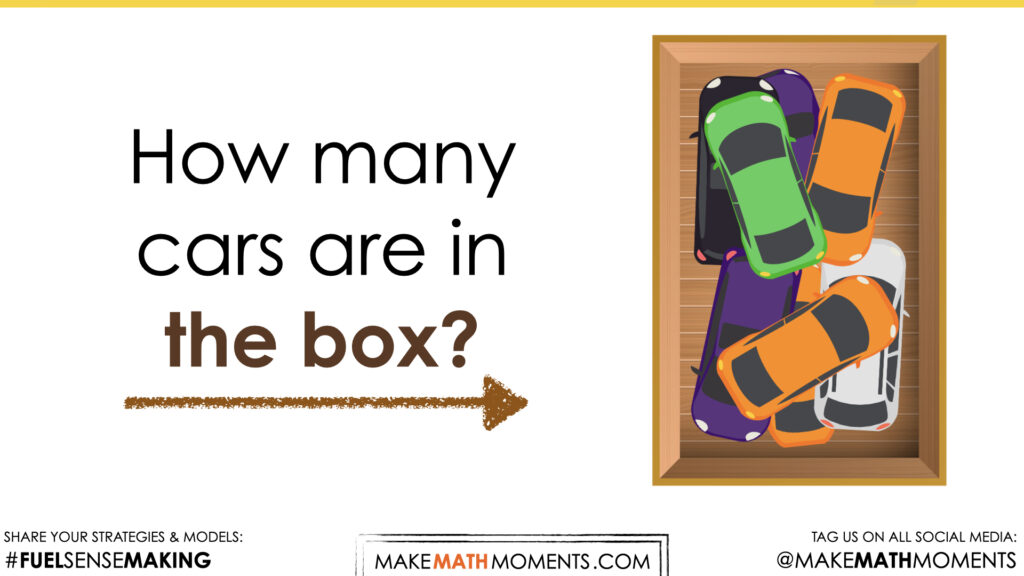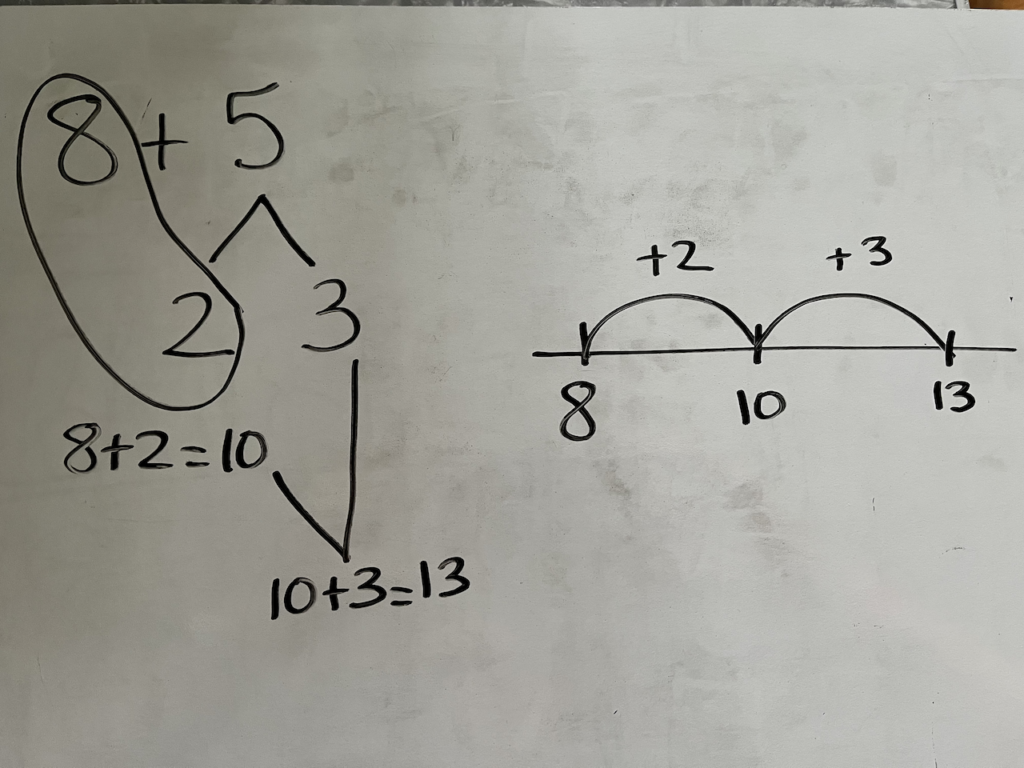COUNTING CARS
ADDITION STRATEGIES: COUNTING ON
Explore addition through the strategy of counting on and the part whole model.
Intentionality
Spark Curiosity
Fuel Sensemaking
During Moves
Student Approaches
Next Moves
Consolidation
Reflect and Consolidation Prompts
Resources & Downloads
Educator Discussion Area
Intentionality & Unit Overview

Length of Unit: 5 Days
Access each lesson from this unit using the navigation links below
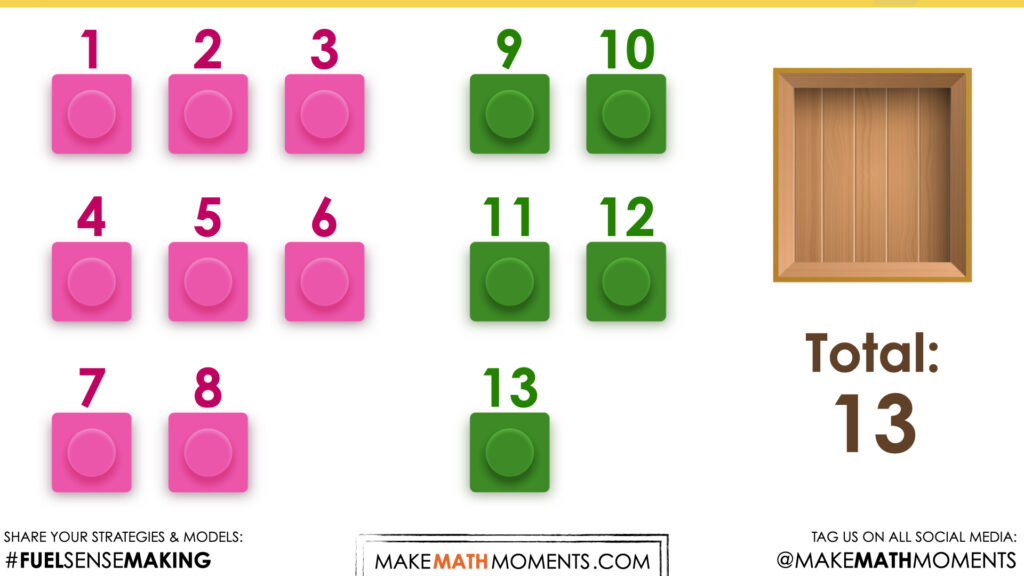
Students will estimate the number of cars in the box. They will also explore the addition situation “Join: result unknown”.
In this task, students will explore estimation, quantity, the addition strategy of counting on and the part whole relationship.
Big ideas of the unit:
- Addition names the whole in terms of the parts: when the parts of a set are known we call it addition
- The part whole relationship is connected to addition as numbers are composed of two or more parts
- Addition can be used in action (or active) situations (i.e.: joining and separating) and static (or passive) situations (i.e.: part part whole)
- Different addition situations will elicit different strategies
- Number relationships provide the foundation for strategies to help students remember basic facts
- Student estimation of small amounts and understanding of quantity as the amount of objects
- Using the part whole model to understand the unknown parts of a problem. The unknown identified which operation needs to be used to solve the problem
- Provide students an opportunity to visualize a situation then interpret which operation is needed to solve word problems
- Models can be used to connect concrete to abstract
- Explore addition strategies and provide opportunities for students to move from “direct modelling and counting all” to using counting on as a strategy to solve addition problems. Counting on is an important development as students work with bigger numbers, so students do not have to model both numbers in the question
Spark Curiosity
What Do You Notice? What Do You Wonder?
Show students this video:
Then, ask students:
What do you notice?
What do you wonder?
Ask the students to share some of their notice and wonderings with their neighbours for about 60 seconds.
Finally, allow students to share with the entire group. Be sure to write down these noticings and wonderings on the blackboard/whiteboard, chart paper, or some other means to ensure students know that their voice is acknowledged and appreciated.
Some of the noticing and wondering that may come up includes:
- There are 4 green ones
- There are 2 orange ones
- There are 2 blue ones
- There is 1 black one
- There are tractors
- It is like a rainbow of
- What kind of cars are they?
- I like all of the colours
Estimation: Prompt
Show the following short silent animation in order to introduce the first question we will challenge them with:
How many cars are in the box?
Allow students time to look at the final picture. Consider removing the picture after a short amount of time (5 seconds) to encourage students to make that estimate rather than giving too much time for them to count each one. If students need to see the picture again to confirm an estimation, then show the picture again. Consider asking students to think about a number of cars that would be “too low” and a number that would be “too high” before asking for their best estimate in order to help them come up with a more reasonable estimate. Encourage students to share their estimates, however avoid sharing their justification just yet. We do not want to rob other students of their thinking.
Estimation: Update & Partial Reveal
Celebrate student estimates that were very close to the actual number of cars using a routine of your choice as we head into the sense making portion of this lesson.
Fuel Sense-making
Crafting A Productive Struggle: Prompt
Show the following video to create a context for the students.
It is birthday party time. One of the gifts at the party is going to make the birthday boy very happy.
He receives a gift from his Great Aunt. He knows his Great Aunt always gives the best gifts so he rips it open immediately. Sure enough, inside the bag are 5 more cars! He grabs the box of cars that he already has and wants to know how many cars he has now.
How many cars are there now?
During Moves
While Students Are Productively Struggling…
Use this time to monitor student approaches to be used for consolidation. Thinking about which strategies will be selected and how they will be sequenced during consolidation discussion.
- most accessible to least accessible solution strategies and representations;
- most common/frequent to least common/frequent strategies and representations; or,
- choose another approach to selecting and sequencing student work.
Tools to have available to students:
- blocks or small manipulatives
- Whiteboard and marker
- part part whole mat
- number lines
Ask students to share their strategies for how many cars are in the box.
Assessment:
This checklist can be used for tracking formative assessment as students are working. The information collected can be used to form whole group, small group or one-to-one support models.
Student Approaches
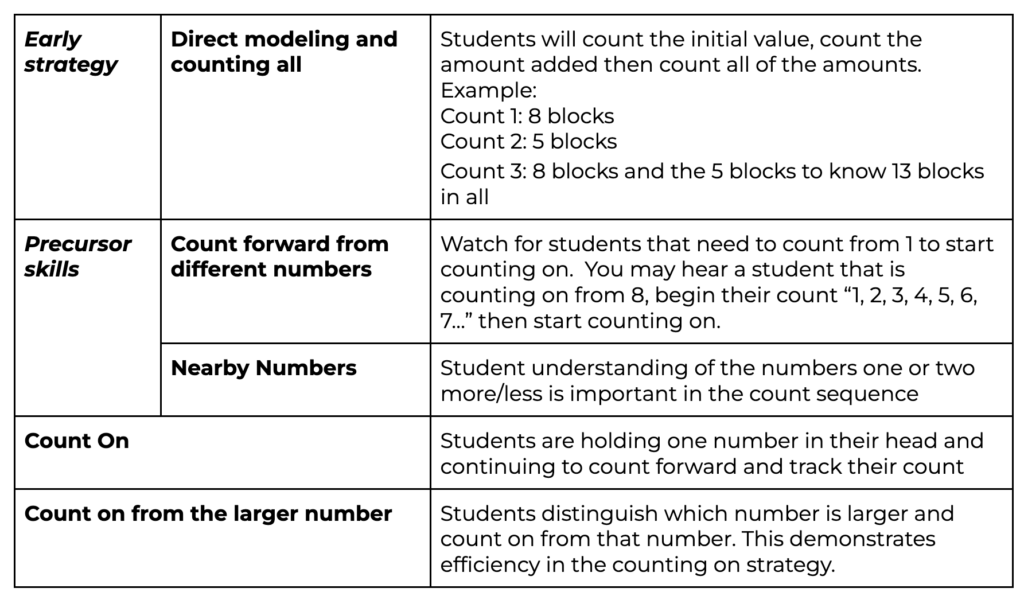
Student Approach #1: Direct Modeling and Counting All
I counted out 8 blocks to represent the 8 cars in the box. I counted out 5 more blocks to represent the amount of cars that were given in the birthday present. I went back and counted all of the blocks starting at 8.
Note: This strategy is called counting 3 times because of the 3 counts that the student is making.
Count 1: 8 blocks
Count 2: 5 blocks
Count 3: 8 blocks and the 5 blocks
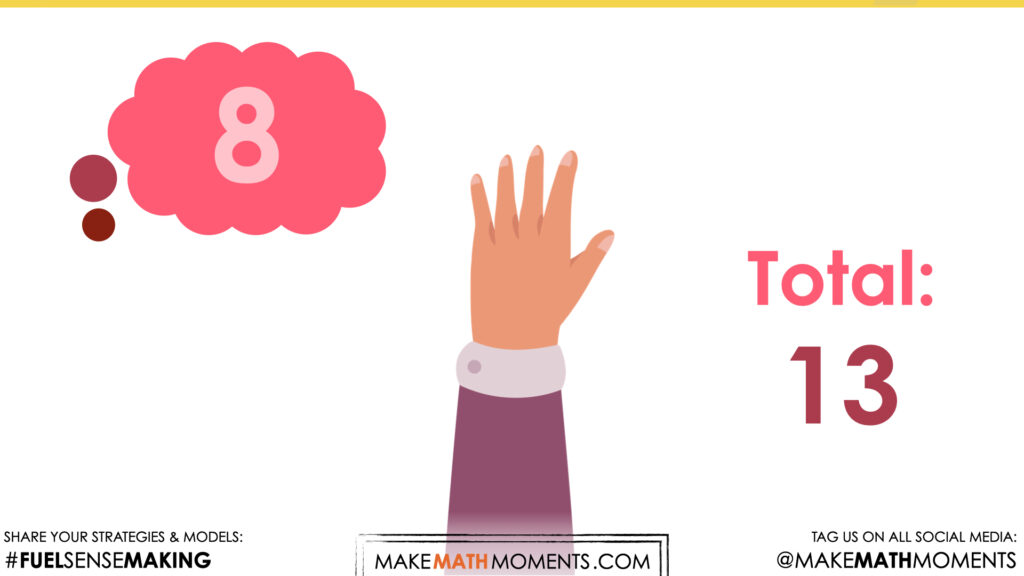
Student Approach #2: Counting on using Fingers
I held the number of cars that I have before the birthday present in my head (8) then I counted on the 5 more cars.
Note: This strategy can vary slightly by watching the student’s fingers as they are counting on. Does the student need to have a pre counted model of 5 to count on? Or can the student track the 5 as they are counting?
Students may also count on from the larger amount. This demonstrates an understanding of the commutative property: changing the order of the addends does not change the sum.
Student Approach #3: Counting On Using a Number line
I found 8 on the numberline then I counted on 5 more. I got to 13 so that is how many cars the child has now.
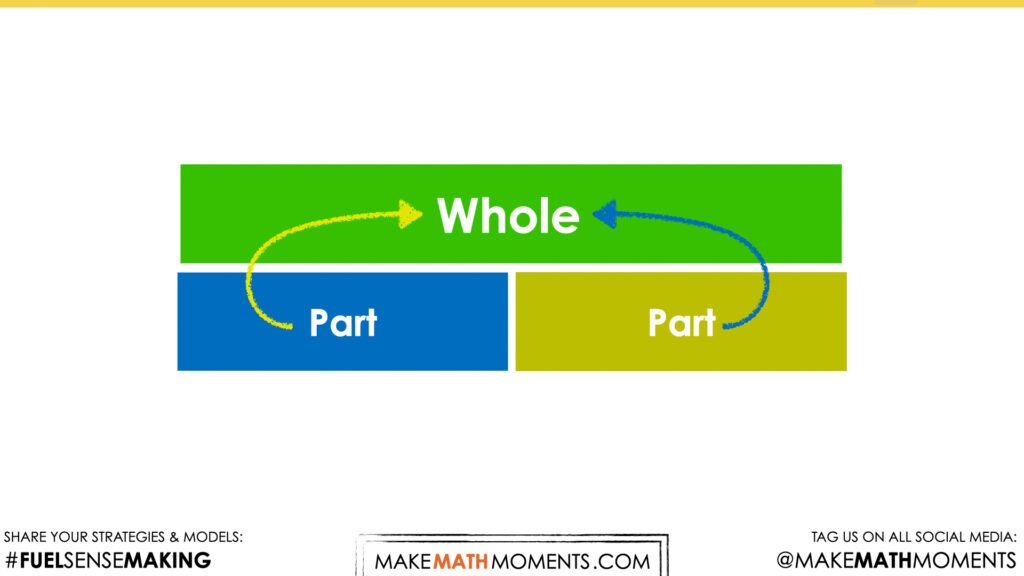
Student Approach #4: Part whole mat
This strategy might be used if a classroom has been practicing use the part-part-whole mat to model where the unknown is for the question. In this case, the student would represent/write 8 in one “part” then represent/write 5 in the other “part”. In this case, the whole is unknown. The student will still have to use a strategy to add the numbers but the PPW mat can be used to help the student navigate which operation they will need to use to solve the question.
Student Approach #5: Up and Over Ten
This strategy uses the part-whole idea again but decomposes (breaks apart) the numbers in the question. As shown on the number line, a student could start at 8 then break apart the 5 into numbers that are more accessible without counting on. In this case, a student could think about bonds of ten to use 2 from the 5 to make 10 then add three more to make 13.
Another option is that a student would start at 5 and break apart the 8. Some students are easily able to “find the 5” in a number. In this example, a student would use their doubles fact of 5 + 5 to make 10. Then there would be 3 more from the 8 to add on.
Note: This requires lots of key ideas for the student to have:
- PPW (breaking up the 5)
- Bonds of ten (8 +2)
- Adding to a decade number
Next Moves
Consolidation
When selecting student responses, consider your learning goal. This may vary depending on grade level. This question will elicit counting on, but it can also be used in discussion with the beginning stages of Up and Over ten.
When sequencing student responses, consider the order that will best lead to the learning goal. If a student response does not come up when monitoring student work, consider demonstrating that response and which skills/activities students need to lead them the targeted strategy.
The purpose of the consolidation is to generalize addition as the combination of two parts.
If a student has modeled the situation using a part-whole mat, consider showing that strategy first to show how the student used the context to fill in the part-whole mat. Consider asking students how we know which number goes with which portion of the mat? If a student did not use a part-whole mat, it could be done during this consolidation phase. Demonstrate that the two amounts would come together to make a whole.
Direct modeling (the student uses concrete materials or a drawing to help solve the problem) and counting all (the student uses concrete materials or drawings to model all of the numbers in the problem and then counts all of the items represented) is a starting point for any student. It is an important stage and shows that students do understand the context of the question. The goal of this lesson/unit is to encourage students to move away from counting all and into storing one number and only having to track one amount. Direct modeling is still an important phase and is often a phase that students will use when the numbers become bigger or situation type is harder. Therefore, still value this strategy by showing a student who has used it.
This video may be use to support demonstrating “Direct Modelling and counting all”:
The counting principle of cardinality (the last number stated when counting a group of objects represents how many objects there are) may need to be explored to support a transition from direct modelling and counting all to counting on. When a student has developed the understanding of cardinality, a consolidation of the direct modelling and counting all strategy could be questioned with “Do we need to count these objects again if we already know that there are ____ of them?”.
Click here for more information on the counting principles.
As a way to move students towards counting on, consider using an action. The goal of counting on is to start counting from one amount and give each item in the second amount an additional count.
Demonstrate how students can use an action to support remembering one of the counts by “placing one number in their head”. Show the movement of touching your hand to your head as you say the number out loud.
“We have 8 cars, I am going to put that number in my head so I don’t forget” (demonstrate that action and have the students try it too).
This video may be used to demonstrate counting on using fingers as trackers:
Highlight options for students to be about to count on the other amount. By using student strategies, show how students can use their fingers to track the second amount or a numberline (draw one or use classroom number line).
This unit continues with additional opportunities for students to practice counting on.
Consult the assessment tracker used during the Sense Making portion. Did students have a strategy? Were students able to at least direct model? It is possible that not all of the students were observed/talked to during the Sense Making portion, ensure that those students are observed/talked to first on day 2. As the unit progresses, this data will be used to inform instruction and create small group/ whole class support.
Reflect and Consolidation Prompts
Provide students an opportunity to reflect on their learning by offering these consolidation prompts to be completed independently.
Consolidation Prompt #1:
How can the counting on strategy make adding more efficient?
Consolidation Prompt #2:
Try using the counting on strategy to solve this question:
7 + 5
We suggest collecting this reflection as an additional opportunity to engage in the formative assessment process to inform next steps for individual students as well as how the whole class will proceed.
Resources & Downloads
Printable Lesson Plan PDF
Videos, Images & Media Files
Apple Keynote Presentation
Powerpoint Presentation
Printable Consolidation Prompts
Educator Discussion Area
Login/Join to access the entire Teacher Guide, downloadable slide decks and printable handouts for this lesson and all problem based units.
Explore Our 60+ Problem Based Units
This Make Math Moments Lesson was designed to spark curiosity for a multi-day unit of study with built in purposeful practice, number talks and extensions to elicit and emerge strategies and mathematical models.
Dig into our other units of study and view by concept continuum, grade or topic!