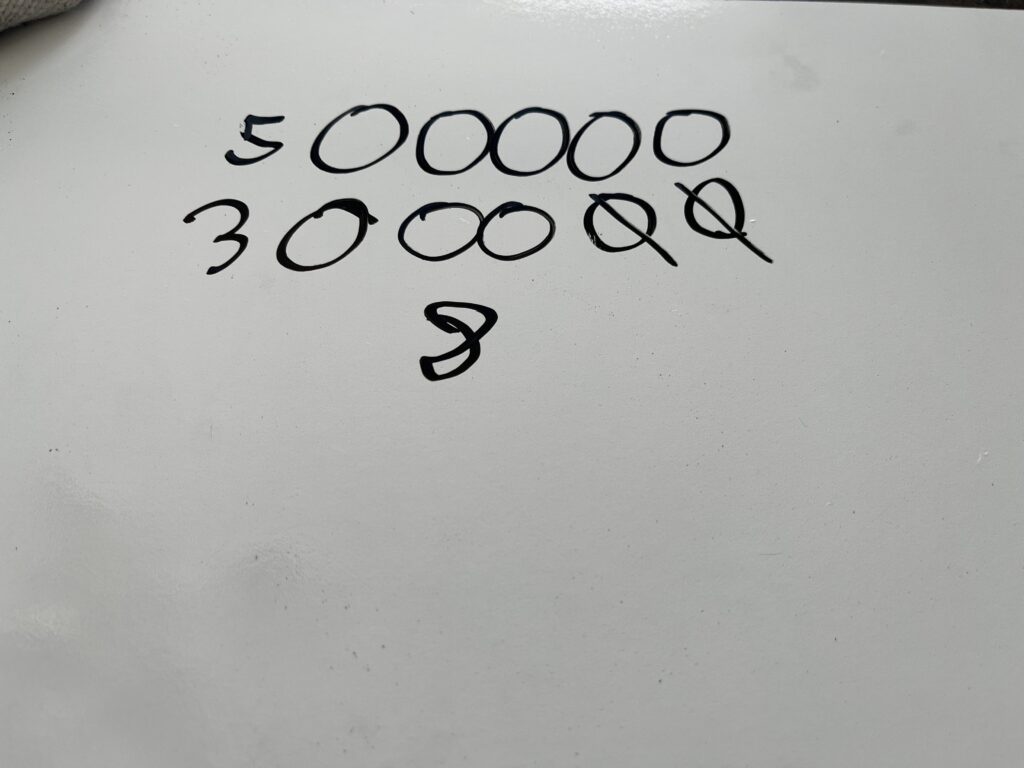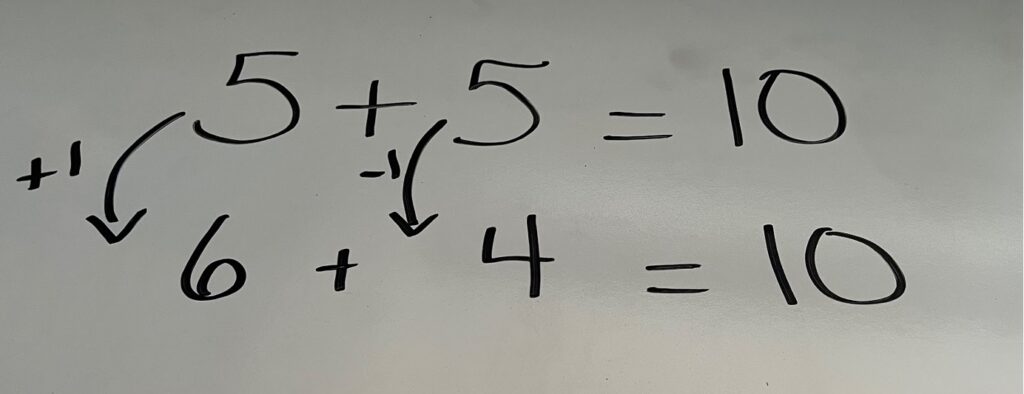BOWLING PINS
ADDITION STRATEGIES: BREAKING APART TO MAKE TEN
Explore addition through the strategy of breaking apart to make ten.
Intentionality
Spark Curiosity
Fuel Sensemaking
During Moves
Student Approaches
Next Moves
Consolidation
Reflect and Consolidation Prompts
Resources & Downloads
Educator Discussion Area
Intentionality & Unit Overview

Length of Unit: 5 Days
Access each lesson from this unit using the navigation links below
Students will estimate the number of bowling pins knocked down. Then students will build initial understanding of ten by exploring bowling pins and the vicious 7-10 split.
Intentionality…
In this task, students will explore combinations of ten in a context through an estimation prompt. This will allow for an opportunity to recognize 10 as an anchor and the relationship between the numbers that compose to make 10.
Big ideas of the unit:
- Understanding hierarchical inclusion allows for flexible composing and decomposing of numbers
- Numbers can be decomposed by separating a whole into two or more parts
- Addition names the whole in terms of the parts: when the parts of a set are known we call it addition
- Different addition situations will elicit different strategies
- Number relationships provide the foundation for strategies to help students remember basic facts
- Commutative and Associative property of addition can be used to help learn facts
- Models can be used to connect concrete to abstract
Spark Curiosity
What Do You Notice? What Do You Wonder?
Show students the following video:
Then, ask students:
What do you notice?
What do you wonder?
Ask the students to share some of their notice and wonderings with their neighbours for about 60 seconds.
Finally, allow students to share with the entire group. Be sure to write down these noticings and wonderings on the blackboard/whiteboard, chart paper, or some other means to ensure students know that their voice is acknowledged and appreciated.
Some of the noticing and wondering that may come up include:
- It is a bowling alley
- All of the pins were knocked down in one shot
- All of the pins down is called a strike
- There are ten bowling pins
- 10 bowling pins knocked down
- The ball is rolling
Estimation: Prompt
After we have heard students and demonstrated that we value their voice, we can land on the first question we will challenge them with a quick estimation prompt video:
Then students will be prompted with the following estimation prompt:
How many bowling pins are still standing up?
Make an estimate.
Allow students time to look at the final picture. Consider removing the picture after a short amount of time (5 seconds) to encourage students to make that estimate rather than giving too much time for them to count each one. If students need to see the picture again to confirm an estimation, then show the picture again.
It might be helpful to remind students that there are 10 pins in each lane before the shot. Consider asking students before asking for their best estimate in order to help them come up with a more reasonable estimate:
What number of pins knocked down would be too low?
What number of pins knocked down would be too high?
Encourage students to share their estimates, however avoid sharing their justification just yet. We do not want to rob other students of their thinking.
Estimation: Update & Reveal
Share the following estimation reveal video:
Celebrate student estimates that were very close to the actual number of cars using a routine of your choice as we head into the sense making portion of this lesson.
Fuel Sense-making
Crafting A Productive Struggle: Prompt
Next, we will leverage storytelling in combination with a silent animation video as a means to create context for students.
Here is a potential script you could use to create the storyline while playing the video down below:
Over the weekend I went 10-pin bowling. It was a great game until I hit a shot known as the “7 – 10 split”. This shot is considered one of the hardest shots in bowling.
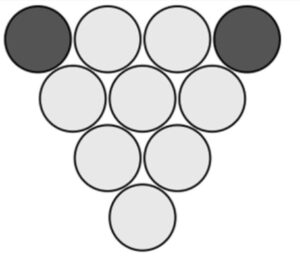
Facilitator Notes: In 10 pin bowling, the bowling pins are set up in a triangle arrangement and each pin is referred to as a number 1-10.
The “7-10 split” refers to the 2 bowling pins in the back left and back right of the lane that are still standing after the first shot. They are pin #7 and pin #10. So the name comes from the fact that after the shot, those two pins are still standing.
This shot is so tricky because it is hard to get the ball to hit one of the pins and then go across the lane to hit the other pin.
Picture below for reference:
Below is the video you can play while verbally sharing the storyline regarding the 7-10 split. As the video is playing be prepared to pause the video after the prompt:
How many pins?
Pause video to confirm with students that there are 10 pins standing. Consider asking students how they knew there were 10 pins:
Possible responses:
- count by 1s
- count by 2s
- subitized small amounts and added them together
It is necessary for the students to know that there were initially 10 pins before continuing to play the video. The next part of the video reveals the struggle prompt:
How many pins were knocked down?
During Moves
While Students Are Productively Struggling…
Since the number is inside of 10, it is possible that students will use their fingers as a tool. Watch how students are using their fingers and pose purposeful questions to determine student reasoning.
- Do they know the amount on their fingers without counting?
- Possible prompt: “Show me 6 fingers.” Do students have to count each finger to make 6?
- When both hands are being used, how do they keep track the count? Often students will nod along tracking the count in their head or a more tactile approach of tapping their nose with each finger as they say the count.
Encourage students to demonstrate their thinking on their fingers by drawing on a whiteboard or discussing orally.
As students are working, monitor approaches that will be used during the consolidation of this question. Consider consolidating a variety of strategies that are selected and sequenced based on:
- Most accessible to least accessible solution strategies and representations;
- Most common/frequent to least common/frequent strategies and representations;
Tools to have available to students:
- Blocks or small manipulatives
- Whiteboard and marker
- Ten frames
Ask students to share their strategies for how many pins were knocked down.
Assessment tool:
A tracking tool such as a checklist may be useful to gather evidence of student thinking. The checklist can then be used to create small groups or individual support as student needs become apparent. It is likely that a student will not have information under each column of the assessment tracker but provides a consolidated space for evidence gathering.
| Pre-cursor skills | ||
| Finger recognition | Students are able to recognize the number of fingers they are holding or hold up an amount on their fingers without having to count | |
| Early strategy | Direct modeling and counting all | Students will count the initial value, count the amount added then count all of the amounts. Example: Count 1: 6 bowling pins Count 2: 4 bowling pins blocks Count 3: 6 bowling pins and the 4 bowling pins to know 10 bowling pins in all |
| Count On | Students are holding one number in their head and continuing to count forward and track their count | |
| Count on from the larger number | Students distinguish which number is larger and count on from that number. This demonstrates efficiency in the counting on strategy. | |
| Using another known fact | Students are using another combination to assist. E.g., using the 5 + 5 doubles fact to help with 6 + 4 | |
| It is a known fact | Student can automatically recall a matching combination of 10 | |
Student Approaches
Student Approach #1: Direct Modeling and Counting All
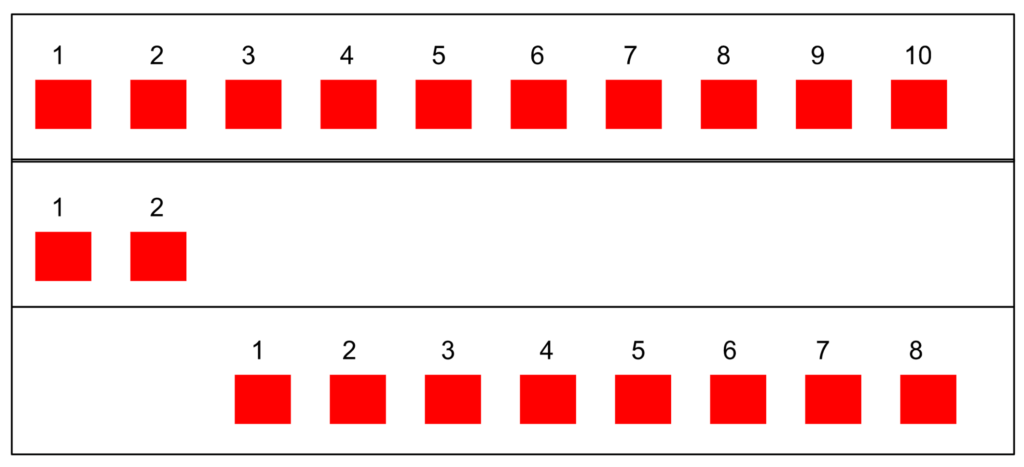
I counted out 10 blocks to represent the 10 bowling pins at the start. I pulled 2 blocks to the side to represent the 2 bowling pins left. I counted the number of blocks left.
- Count 1: 10 blocks
- Count 2: 2 blocks
- Count 3: 8 blocks
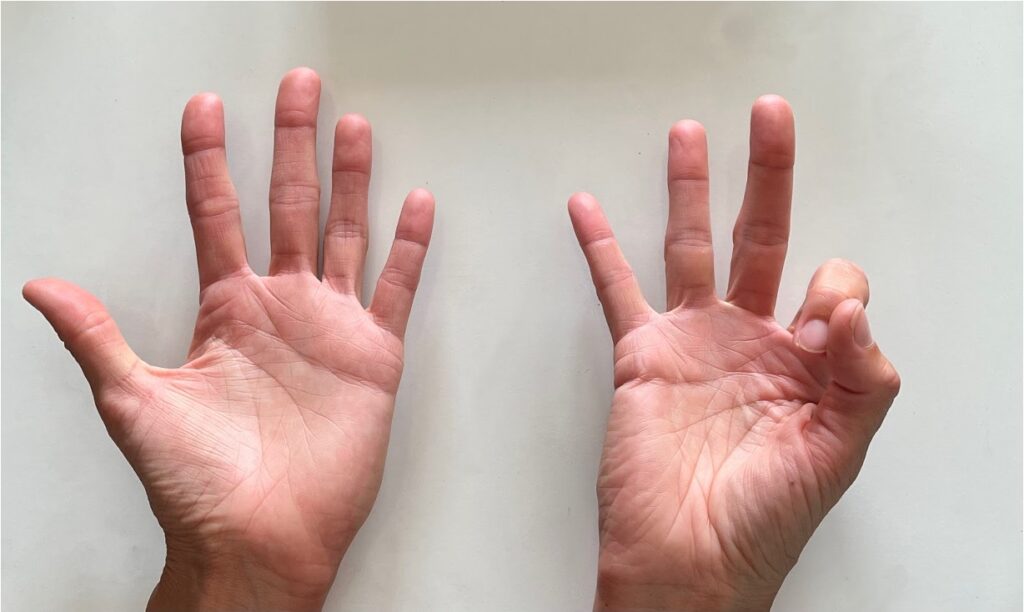
Student Approach #2: Adding up using fingers
I held up 10 fingers because that is how many pins there are. I put down two fingers then knew there was 8 fingers left.
Facilitator Note: This strategy might also be done but the student will count the remaining fingers one by one. Since both hands are preoccupied, the student may tap the fingers on their desk or tap their fingers to their nose as they track the count.
Student Approach #3: Pictorial and direct modelling with a ten frame
I drew 10 circles like a ten frame. I crossed off 2 of the circles because there were two pins standing up. I knew that there were 5 in the top row and 3 in the bottom row. 5 and 3 make 8. So there were 8 pins knocked down.
Student Approach #4: Known fact
I know that 2+8 make 10.
Depending on the exposure of the combinations of 10, students may have the patterns memorized already.
Student Approach #5: Subtraction
I know that 2+8 make 10.
There was 10 pins and then 2 were left still standing. Since 10-2 = 8, there must be 8 pins that were knocked down.
Next Moves
Reveal
Depending on how you consolidated the learning by using student solution strategies, you may or may not feel these reveal videos are helpful.
However, if you are just learning to model student thinking and feel it could be helpful for students to see thinking represented visually, consider the following reveal video.
Alternatively, you might consider sharing the final frame of the reveal video:
Consolidation
This Sense Making opportunity is a subtraction structure with the “change unknown”. This means that the starting amount of 10 pins is “known” then we subtract some pins and now there are two left. It could be modelled with this number sentence: 10 – ___ = 2
Although this is a subtraction question structure, students may use an “add up” strategy to find the unknown. When selecting student responses, consider your learning goal. This may vary depending on grade level.
The task provides exposure to composing ten but also to a subtraction question structure that may challenge student thinking. The numbers in this problem will be accessible in a variety of classrooms, so a more challenging question structure is an opportunity to expose students to different types of questions. For more information about addition and subtraction question structures: https://mathisvisual.com/adding-subtracting/
When sequencing student responses, consider the order that will best lead to the learning goal. If a student response does not come up when monitoring student work, consider demonstrating that response and which skills/activities students need to lead them the targeted strategy.
The purpose of the consolidation is to demonstrate strategies that students can use when solving a question involving the decomposition of 10 or the combinations of 10. Student understanding of the combinations of 10 (7+3, 6+4, etc) is considered one of the most important strategies (Van de Walle, 2018). The base ten pattern of the number system allows students to use the known combinations of 10 as they solve increasingly complex questions.
A very common tool that students will use is their fingers. Recognizing how students are using their fingers will provide an insight into development as well. In the case of this question, as demonstrated in student approach number one, a student may hold up 10 fingers then put down two to represent the pins that are still standing. The student will then count each of the remaining fingers to find the answer.
If you notice that a student has to recount their fingers, consider some intervention work to support finger recognition.
Possible intervention practice: Finger Recognition
If students need support with finger recognition, provide practice with this by asking the students to show different amounts on their fingers.
E.g.
“Using only one hand, show me 4 on your fingers.
Student may count out 4 fingers.
“How would 4 look if you had to use both of your hands?”
Student shows 3 on one hand and 1 on the other. Or students shows 2 on one hand and 2 on the other.
This is different from a student who holds up 10 fingers then puts down two but can recognize the remaining 8 fingers without having to count. This strategy is more sophisticated than a student counting each of their fingers.
There has been a lot of discussion around finger recognition and the use of fingers in the math class. Children are asked questions related to numbers their whole life so use of fingers is a strategy that will be very natural. When asked, “How old are you?”, even from a very young age children will hold up their fingers to represent the amount. Considering the numbers in the combinations of 10, the use of fingers should not be discouraged.
To transition from direct modelling and counting all, encourage students to use their fingers to track as they “count on”. A student that counts on, stores one amount in their head and counts on the other amount. In this case, a student would store “2” in their head and count on 8 more to get to 10.
Some students may also have some of the combinations of 10 as known facts. The doubles fact of 5+5 can be utilized here for the understanding of some facts close by. E.g. “I know 5+5 so if I can take one from 5 and add one to the other 5. This would make 6+4!”
If a student is sharing this strategy with the class, consider demonstrating their thinking with a number sentence so the class can “see” where the amounts are going.
Consult the assessment checklist used during the Sense Making portion.
- Do students have a strategy?
- Were students able to at least direct model?
It is possible that not all of the students were observed/talked to during the Sense Making portion, ensure that those students are observed/talked to first on day 2. As the unit progresses, this data will be used to inform instruction and create small group/ whole class support.
Elementary and Middle School Mathematics: Teaching Developmentally. John Van de Walle, et al. 2018.
Reflect and Consolidation Prompts
Provide students an opportunity to reflect on their learning by offering these consolidation prompts to be completed independently.
Consolidation Prompt #1:
How does knowing 2 + 8 help when trying to solve 8 + 2?
Consolidation Prompt #2:
How many pins would have been knocked down if there were 4 pins still standing?
We suggest collecting this reflection as an additional opportunity to engage in the formative assessment process to inform next steps for individual students as well as how the whole class will proceed.
Resources & Downloads
Educator Discussion Area
Login/Join to access the entire Teacher Guide, downloadable slide decks and printable handouts for this lesson and all problem based units.
Explore Our 60+ Problem Based Units
This Make Math Moments Lesson was designed to spark curiosity for a multi-day unit of study with built in purposeful practice, number talks and extensions to elicit and emerge strategies and mathematical models.
Dig into our other units of study and view by concept continuum, grade or topic!