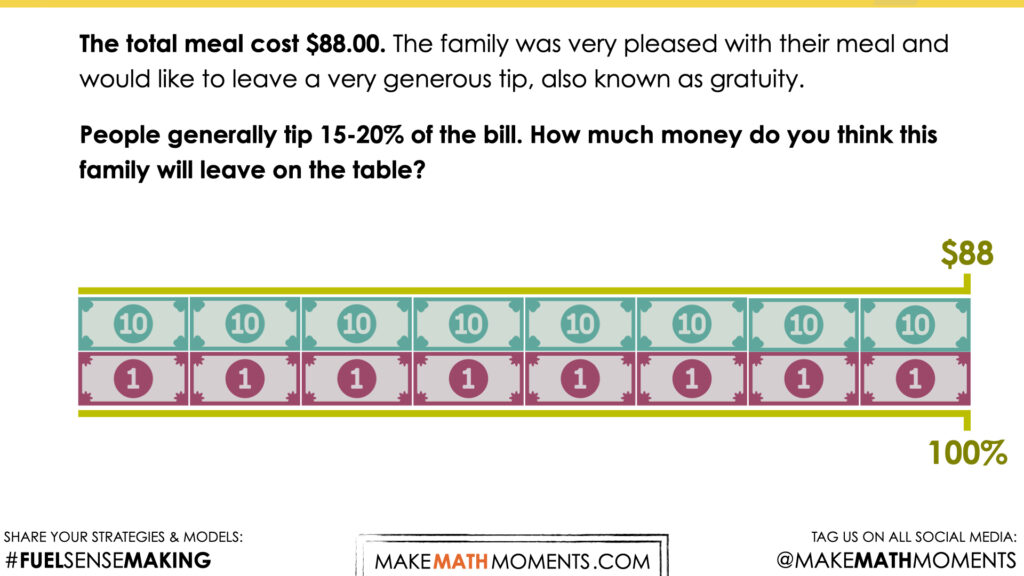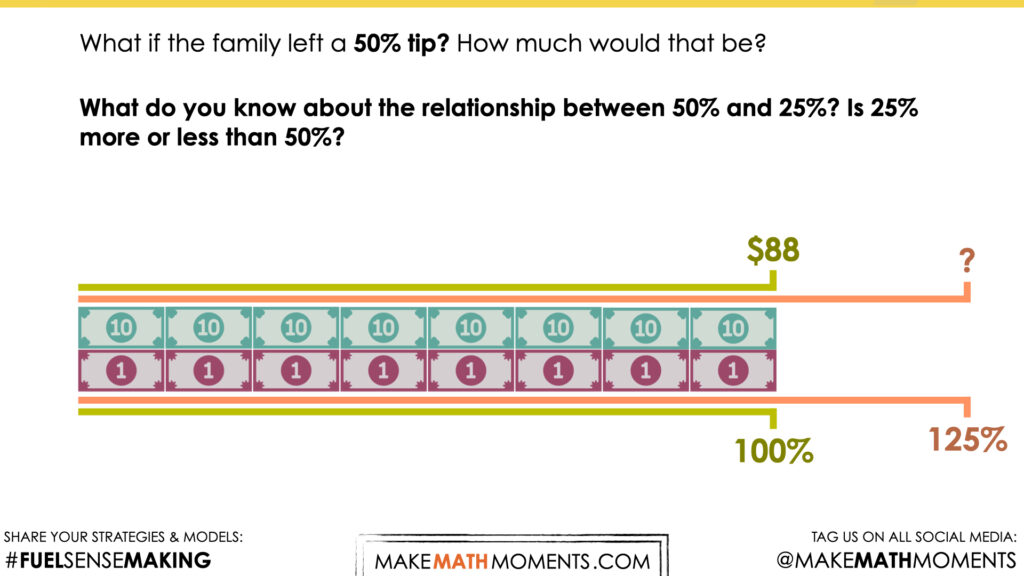BIG TIPPER
PERCENT AND FINANCIAL LITERACY
Investigate strategies to increase and decrease a whole number by a percent.
Intentionality
Spark Curiosity
Fuel Sensemaking
During Moves
Student Approaches
Next Moves
Consolidation
Reflect and Consolidation Prompts
Resources & Downloads
Educator Discussion Area
Intentionality & Unit Overview
Length of Unit: 5 Days
Access each lesson from this unit using the navigation links below
Students will explore the concept of gratuity using a benchmark percent as an operator.
In this task, students will begin exploring financial literacy concepts that require a percent as an operator. On Day 1, students will investigate the idea of gratuity. A bar model will be introduced to position students to think about gratuity, leaving a tip, as a percentage relative to the total cost of the meal. Some of the big ideas that may emerge in today’s lesson include:
- Fractions, decimals, and percents can all represent relationships to a whole;
- Any fraction, decimal or percent can be used as an operator;
- Increasing by a given percent means the percent is added to the whole;
- A bar model is helpful for representing a situation that involves a percent increase.
Spark Curiosity
What Do You Notice? What Do You Wonder?
Show students this video:
Then, ask students:
What do you notice?
What do you wonder?
Give students 60 seconds (or more) to do a rapid write on a piece of paper.
Then, ask students to share with their neighbours for another 60 seconds.
Finally, allow students to share with the entire group.
Some of the noticing and wondering that came up in a class recently included:
- I notice a receipt.
- I notice there are different items of food and the cost.
- I wonder if five people went out for dinner.
- I notice money being placed on the table.
- I notice the total is $88.
- I wonder if there is tax.
At this point, you can answer any notices and wonders that you can cross off the list right away. For example, five family members went out for dinner. The total cost of their meal is $88. Tax was included.
Estimation: Prompt
Next, share the following short animation or visual prompt and ask the following question:
Prompt students with:
The total meal cost $88.00. The family was very pleased with their meal and would like to leave a very generous tip, also known as gratuity. People generally tip 15-20% of the bill. How much money do you think this family will leave on the table?
We can now ask students to make an estimate (not a guess) as we want them to be as strategic as they can possibly be. This will force them to use reasoning to justify an amount.
While Students Are Estimating…
Monitor student thinking by circulating around the room and listening to the mathematical discourse. Encourage students to use precise mathematical language and listen for the use of fractional language or percent to describe the total amount of money left for the bill. Listen for the use of benchmark percentages such as 10%, 20%, 25% or 50%. In today’s task, students will be encouraged to leverage the relationship between fractions and percent.
The purpose of the estimate is to encourage students to start thinking about percent relative to the whole. The whole in this case being $88.00. Estimation is a useful strategy when exploring financial literacy concepts involving percent.
Allow students to share and justify their estimates with a neighbour first, then with the class. Write down their estimates on the chalkboard/whiteboard/chart paper so students feel their voices are being heard and so they feel they have a stake in solving this problem.
Fuel Sense-making
Crafting A Productive Struggle: Prompt
Since you have already taken some time to set the context for this problem and student curiosity is already sparked, we have them in a perfect spot to help push their thinking further and fuel sense making.
Share the following silent animation.
You can verbally share the following prompt with students:
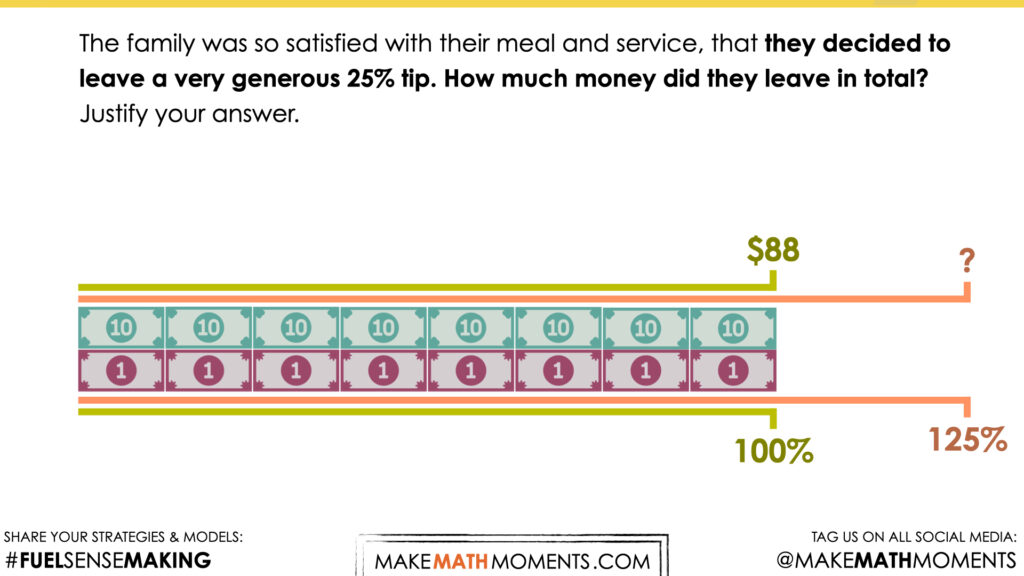
The family was so satisfied with their meal and service, that they decided to leave a very generous 25% tip.
How much money did they leave in total?
Justify your answer.
During Moves
While Students Are Productively Struggling…
Monitor student thinking by circulating around the room and listening to the mathematical discourse. Select and sequence some of the student solution strategies and ask a student from the selected groups to share with the class from:
- most accessible to least accessible solution strategies and representations;
- most common misconceptions;
- most common/frequent to least common/frequent representations; or,
- choose another approach to selecting and sequencing student work.
The strategies you might see students use include:
- Partitioning the bar in fourths, and the adding on.
- Fair sharing in four parts, and then adding a fifth part (five fourths).
- Halving.
- Using an algorithm.
In order for students to solve this problem without the use of a calculator, it will be critical that students understand that 25% is equal to one-fourth. If students do not demonstrate an understanding of this relationship, pose the following purposeful question:
What if the family left a 50% tip? How much would that be?
What do you know about the relationship between 50% and 25%? Is 25% more or less than 50%?
Have students share their reasoning for determining the total amount of money left for this dinner bill.
Discuss their thinking during your consolidation to build off of their current prior knowledge and understanding rather than “fixing” or “funnelling” student thinking to a representation and justification that does not connect to their understanding.
Student Approaches
Student Approach #1: Fair Sharing
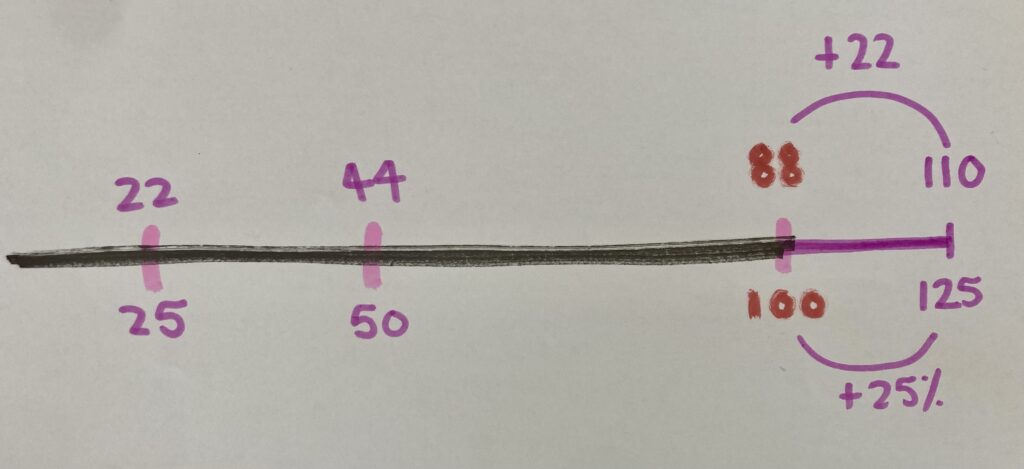
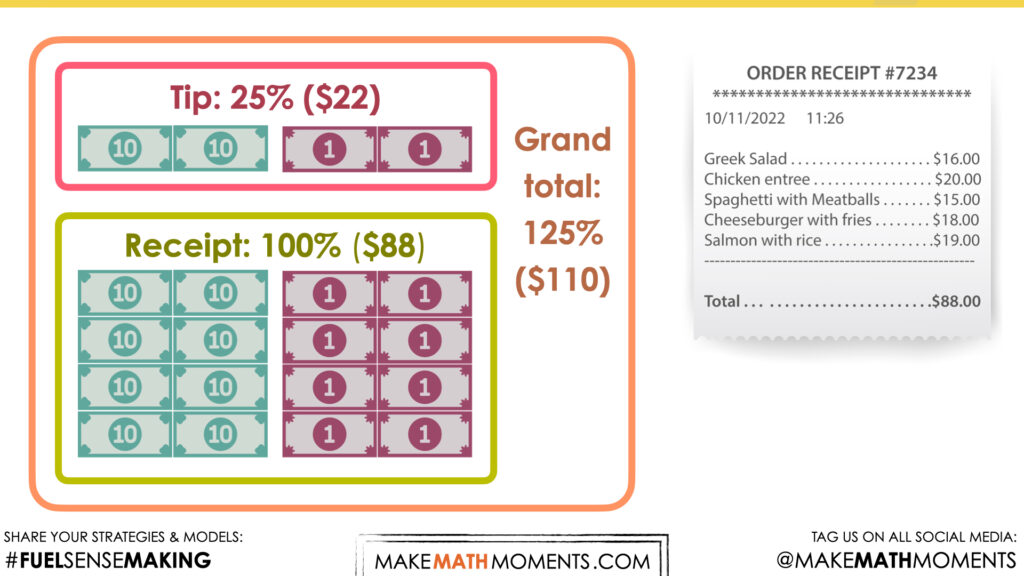
I know that 25% is the same as one quarter. So I made four groups, and divided the money between the four groups. I saw that each one-fourth, or 25% is equal to $22. So I know that the family left another $22. That means the total is $88 + $22. The family left $110.
Student Approach #2: Partitioning Through Halving
I started at $88. Then I went to half of that, which is $44. And then half again is $22. I know that 25% is the same as one-quarter, that’s why I split the total bill into quarters. That means they must’ve added another $22 to their bill. That’s a total of $110.
Next Moves
Consolidation
During the consolidation, review the strategies for determining the total amount left for the bill.
As previously mentioned, it is imperative that students understand the relationship between 25% and one-fourth in order to solve this problem using conceptual understanding, without the use of a calculator.
Share a few student solutions to model how to go about determining 25% of $88.00.
Consider sharing the following silent animations:
Startegy #1:
Consider the following strategy for your consolidation:
Strategy #2:
Consider another strategy for your consolidation:
Ask student the following question:
How could I represent this situation as an equation? What operator did we use today?
After student have had an opportunity to discuss with a neighbor, document all the different ways to represent this context symbolically. One of the equations shared might include:
125% x $88 = $110
Many students likely solved this equation using the distributive property of multiplication. For example:
(100% + 25%) x $88 = $110
(100% x $88) + (25% x $88) = $110
Students may also view this context as:
$88 + (25% x $88) = $110
In today’s context, we used percent as an operator to determine a total with gratuity. A big idea that this task serves to reveal is:
- Increasing by a given percent means the percent is added to the whole. So, a 25% increase is 125% of the whole.
The word of in the sentence 125% of the whole is an indicator that the operator in use is in fact multiplication.
Reflect and Consolidation Prompts
Provide students an opportunity to reflect on their learning by offering these consolidation prompts to be completed independently.
Consolidation Prompt #1:
Explain what it means to increase by a percent. Share a few examples.
Consolidation Prompt #2:
Create your own example of a situation involving gratuity. Choose a total bill, the percent you would like to tip. Model and solve for your example.
We suggest collecting this reflection as an additional opportunity to engage in the formative assessment process to inform next steps for individual students as well as how the whole class will proceed.
Resources & Downloads
Printable Lesson Plan PDF
Videos, Images & Media Files
Apple Keynote Presentation
Powerpoint Presentation
Printable Consolidation Prompts
Educator Discussion Area
Login/Join to access the entire Teacher Guide, downloadable slide decks and printable handouts for this lesson and all problem based units.
Explore Our 60+ Problem Based Units
This Make Math Moments Lesson was designed to spark curiosity for a multi-day unit of study with built in purposeful practice, number talks and extensions to elicit and emerge strategies and mathematical models.
Dig into our other units of study and view by concept continuum, grade or topic!