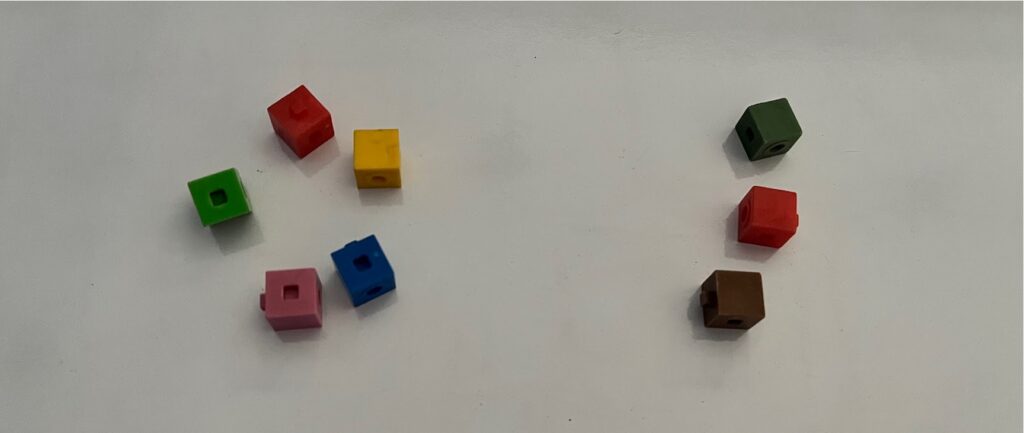BARNYARD
Subtraction: Counting Back and Adding Up
Investigate early subtraction strategies through counting back and adding up to find the difference.
Intentionality
Spark Curiosity
Fuel Sensemaking
During Moves
Student Approaches
Next Moves
Consolidation
Reflect and Consolidation Prompts
Resources & Downloads
Educator Discussion Area
Intentionality & Unit Overview

Length of Unit: 5 Days
Access each lesson from this unit using the navigation links below
In this task, students will begin to explore subtraction and using a natural first strategy of counting back. The numbers used in this lesson will provide an opportunity for students to efficiently use this strategy in a context.
Some of the big ideas that may emerge in today’s lesson include:
- Subtraction names the missing part in terms of the whole
- Counting back is efficient when the count back is small
- Addition and subtraction are related in that addition names the parts in the whole and subtraction uses the whole to find a missing part.
- Subtraction can be used in either take away, comparison, or missing addend situations.
Spark Curiosity
What Do You Notice? What Do You Wonder?
Show students the following video:
Then, ask students:
What do you notice?
What do you wonder?
Give students 60 seconds (or more) to do a rapid write on a piece of paper.
Then, ask students to share with their neighbours for another 60 seconds.
Finally, allow students to share with the entire group.
Some of the noticing and wondering that came up in a class recently included:
- I notice that there is a red barn.
- I notice there are lots of animals
- I wonder if there are more animals in the barn?
- I notice there are 3 chickens
- I notice there are ____ (cows, goats, horses, pigs)
- I wonder if there are any tractors on the farm?
Estimation: Prompt
Next, share the following short animation or visual prompt and ask the following question:
The farmer is closing the barn door for the night.
How many animals does the farmer need to put back in the barn?
We can now ask students to make an estimate (not a guess) as we want them to be as strategic as they can possibly be. This will force them to use reasoning to justify an amount.
While Students Are Estimating…
Monitor student thinking by circulating around the room and listening to the conversations that students are having about the amount of animals that are on the screen.
While students are updating their estimate, listen and observe as students work to make updates. What strategies and mathematical models are students leveraging?
Are they:
- Counting by ones?
- Skip counting?
Allow students to share and justify their estimates with a neighbour first, then with the class. Write down their estimates on the chalkboard/whiteboard/chart paper so students feel their voices are being heard and so they feel they have a stake in solving this problem.
Estimation Reveal
Share the following estimation reveal video:
Fuel Sense-making
Crafting A Productive Struggle: Prompt
Since you have already taken some time to set the context for this problem and student curiosity is already sparked, we have them in a perfect spot to help push their thinking further and fuel sense making.
It has been established that there are 20 animals in the barnyard.
Share the following image and verbally share the following prompt with students:
The pigs are the last animals to be put into the barn.
Three of the pigs are put into the barn. How many pigs still need to be put into the barn?
During Moves
While Students Are Productively Struggling…
Monitor student thinking by circulating around the room and listening to the mathematical discourse. Select and Sequence some of the student solution strategies and ask a student from the selected groups to share with the class from:
- most accessible to least accessible solution strategies and representations;
- most common misconceptions;
- most common/frequent to least common/frequent representations; or,
- choose another approach to selecting and sequencing student work.
Tools to have available to students:
- blocks or small manipulatives
- Whiteboard and marker
- number lines
The strategies you might see students use include:
- Direct Modeling and counting all
- Counting back
- Known addition fact
Facilitator Notes: Tools may include manipulatives, fingers or a number line. When students use a tool, observe how the tool is being used.
Manipulatives:
- Do students count 3 of the objects one by one to remove?
- Are students able to subitize (“see” the amount without counting) 3 and remove in one step?
- Do students count the remaining 5 objects one by one?
- Are students able to subitize 5 as the remaining amount?
For more information about subitizing.
Fingers:
- Do they count their fingers one at a time to figure out how many need to be up to show 8?
- Do the students automatically know how many fingers to hold up to demonstrate 8?
- Do they put down their fingers one at a time to demonstrate 3 pigs?
- Do they automatically put down 3 fingers?
- Do they recognize that they have 5 fingers left without counting?
Number line:
- After finding 8 on the numberline, does the student count back by saying 1, 2, 3 as they are pointing to the numbers? (picture below) This is a transitional stage before counting back. Technically the student is not counting back, but is only counting to 3 and using the number line to direct model. A student that is counting back, has to track 2 counts. They must track the count of 3 while saying each additional count.
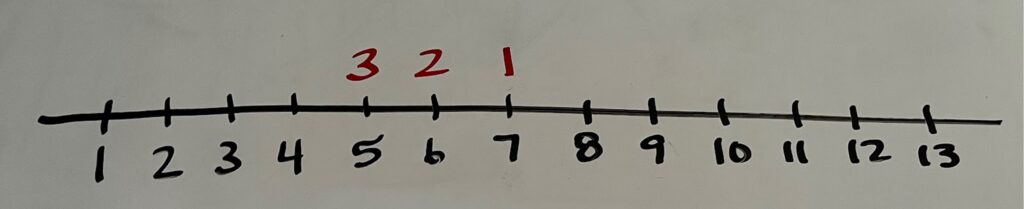
Discuss their thinking during your consolidation to build off of their current prior knowledge and understanding rather than “fixing” or “funnelling” student thinking to a representation and justification that does not connect to their understanding.
Assessment:
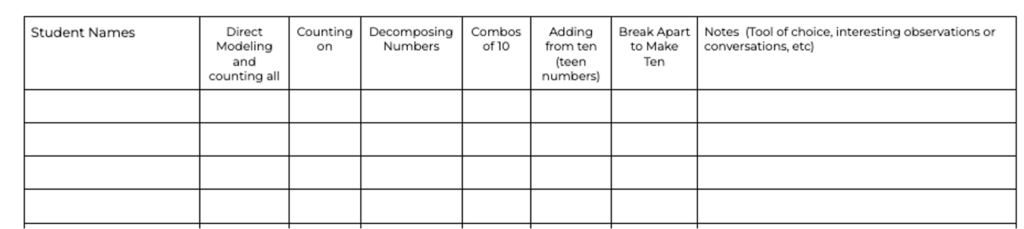
This checklist can be used for tracking formative assessment as students are working. The information collected can be used to form whole group, small group or one-to-one support models.
| Early strategy | Direct modeling and counting all | Students will count the initial value, count the amount added then count all of the amounts. Example: Count 1: 8 blocks Count 2: 5 blocks Count 3: 8 blocks and the 5 blocks to know 13 blocks in all |
| Pre-cursor skills | Count backwards from different numbers | Watch for students that need to count forwards in order to start counting backwards. You may hear a student that is counting back from 8, begin their count “1, 2, 3, 4, 5, 6, 7, 8” then start counting back. |
| Nearby Numbers | Student understanding of the numbers one or two more/less is important in the count sequence | |
| Using the count back strategy | Students are holding one number in their head and continuing to count backwards and track their count | |
| Count up instead | Students are finding the difference/space between in the numbers by adding up from the lower number to the higher number | |
| Strategic and efficient strategy (e.g. Known facts, Down and Under Ten, etc) | Students may start to use known addition facts to support their understanding of subtraction. Students may also use benchmark numbers like 10 when subtracting. The Down and Under Ten strategy is effective when subtracting from a teen number. | |
Student Approaches
Student Approach #1: Skip Counting
I counted out 8 blocks to represent the 8 pigs. I counted 3 of the blocks and moved them to the side. I counted the rest of the blocks, there were 5.
Facilitator Note: This strategy is called counting 3 times because of the 3 counts that the student is making.
Count 1: 8 blocks as the starting amount
Count 2: 3 blocks to remove
Count 3: 5 blocks that are remaining
Student Approach #2: Pouring And Updating
I am thinking about 8.
(Student holds up 1 finger) If 1 pig went into the barn, there would be 7 left.
(Student holds up another finger) If 2 pigs went in the barn, there would be 6 left.
(Student holds up another finger) If 3 pigs went into the barn there would be 5 pigs left.
Student Approach #3: Generalizing a Formula For Volume of a Pyramid
I know that 5 + 3 is 8, so 8 – 3 is 5
Next Moves
Consolidation
During the consolidation, review the strategies for determining the amount of pigs that were left outside of the barn.
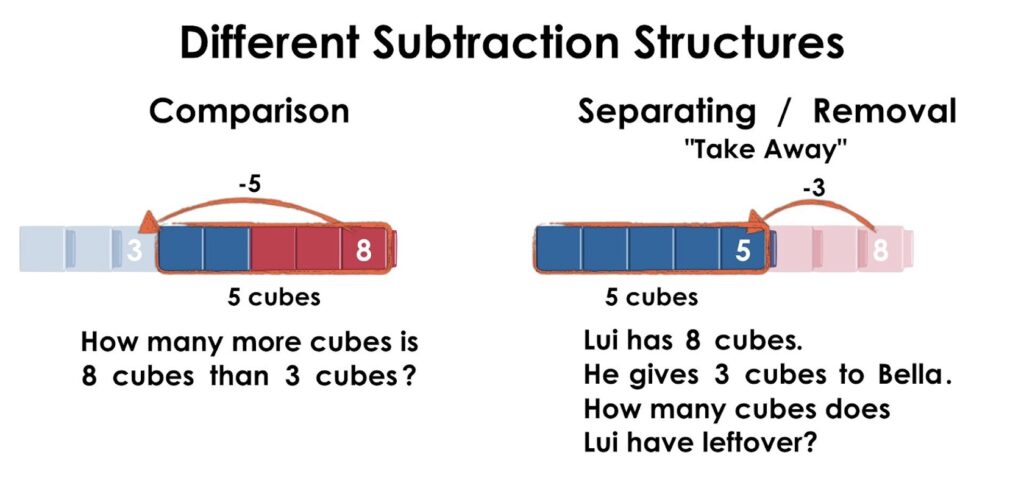
Subtraction is much more complex than addition. It is considered the opposite of addition but there are some subtle differences. Subtraction is often initially introduced to mean “take away” but there are different meanings of subtraction: take away, comparison and part-whole. The names of these meanings vary but overall students need to be exposed to a variety of subtraction situations to help develop fluency. Interestingly enough, it is common for educators to teach students early on that subtraction means take away, when in reality, it only means take away some of the time; particularly when the context involves separating a quantity or removing a part from the whole.
Contexts involving a comparison of two quantities and determining how many more or less one quantity is than the other (or the difference) looks very different than separating / removal / take away:
You may notice that in the comparison situation, the difference is found in the jump, whereas in the separating situation, we see the subtrahend as the jump and the difference is the remaining cubes.
The goal for the consolidation is to discuss counting back. Counting Back is an effective strategy when the count back is small. However, when the count back is larger, such as 23- 18, this strategy is prone to errors. Instead students should be encouraged to use a strategy such as breaking apart the second number or even adding up/counting on to find the difference. Therefore, selecting a particular number is important when presenting a problem. To practice counting back, keep the numbers small such as 5 and under. As students start to subtract higher amounts, counting back becomes more clunky.
Counting backwards in general is difficult for many students, especially when moving beyond 10. Counting forwards is very familiar to most students, particularly when starting from 1. Consider providing opportunities for students to practice counting back from various points. There are activities suggested on Day 2 of this unit.
To introduce symbolism, it can be stated that it is a way to record thinking to a contextual problem. There will be varying exposure to the subtraction symbol in a classroom but students can have an understanding of a subtraction context at a very early age. As early a grade 1, students should start to engage with the subtraction symbol.
For example, “We knew that were 8 pigs outside of the barn, when 3 pigs went into the barn, we figured out that there were 5 pigs left. We can write that using special symbols:
8 – 3 = 5”. The subtraction symbol should be read as “minus” or “subtract” rather than “take away” to eliminate confusion of the different meanings of subtraction.
When modeling an addition problem, each number of the problem can be represented with an object. However, modeling subtraction may pose a problem as it is awkward to model the subtrahend without causing confusion. In the case of this particular scenario, direct modeling the minuend or the whole (8 pigs to start) and then removing the subtrahend (3 pigs to be removed) results in how many pigs remain (5 pigs remain). When you “remove” 3 pigs, you can place them to the side, however a student may easily confuse them to be the number of pigs that remain instead of the number of pigs to be removed from the whole. Confusion is less likely when modeling this same problem on paper as a student may use a crossing out method to demonstrate which part they are removing, while still being able to “see” the subtrahend.
Share a few student solutions to model how they determined how many pigs were left.
Consider sharing the following silent animations:
Counting back
Reflect and Consolidation Prompts
Provide students an opportunity to reflect on their learning by offering these consolidation prompts to be completed independently.
Consolidation Prompt #1:
How could you subtract 1 from a number without counting?
Consolidation Prompt #2:
Create your own subtraction problem involving pigs. How many pigs started and how many pigs went into the barn?
We suggest collecting this reflection as an additional opportunity to engage in the formative assessment process to inform next steps for individual students as well as how the whole class will proceed.
Resources & Downloads
Educator Discussion Area
Login/Join to access the entire Teacher Guide, downloadable slide decks and printable handouts for this lesson and all problem based units.
Explore Our 60+ Problem Based Units
This Make Math Moments Lesson was designed to spark curiosity for a multi-day unit of study with built in purposeful practice, number talks and extensions to elicit and emerge strategies and mathematical models.
Dig into our other units of study and view by concept continuum, grade or topic!