ACORN HOARDING
GROWING & SHRINKING LINEAR PATTERNS
Explore growing & shrinking visual patterns and linear relationships by constructing pattern rules in words, tables of values and equations.
Intentionality
Spark Curiosity
Fuel Sensemaking
During Moves
Student Approaches
Next Moves
Consolidation
Reflect and Consolidation Prompts
Resources & Downloads
Educator Discussion Area
Intentionality & Unit Overview

Length of Unit: 5 Days
Access each lesson from this unit using the navigation links below
Students will analyze a squirrel’s acorn hoarding pattern. They will determine the pattern rule and extend the pattern.
Intentionality…
In this task, students will analyze data based on a squirrel’s acorn hoarding behaviour. They will organize the data. Students will extend the pattern and determine a missing value. Some of the big ideas that may emerge in this lesson include:
- Some patterns are obvious (or easy) to identify, while others are more complex and less obvious.
- Patterns can be extended because they are repetitive by nature.
- Pattern rules are generalizations about a pattern, and they can be described in words.
- A pattern can be extended to make a prediction.
- For far predictions, calculations are required for efficiency.
- In a growing pattern, the values increase.
- In a linear pattern, the values increase at the same rate.
- Graphical representations of linear growing patterns appear as straight lines.
Spark Curiosity
What Do You Notice? What Do You Wonder?
Show students the following video:
Then, ask students:
What do you notice?
What do you wonder?
Give students 60 seconds (or more) to do a rapid write on a piece of paper.
Replaying the video can be helpful here.
Then, ask students to share with their neighbours for another 60 seconds.
Finally, allow students to share with the entire group. Be sure to write down these noticings and wonderings on the blackboard/whiteboard, chart paper, or some other means to ensure students know that their voice is acknowledged and appreciated.
Some of the noticing and wondering that may come up includes:
- I notice there are trees.
- I notice there are days across the top.
- I notice acorns are being dropped on each day.
- I wonder if it’s the same number of acorns every day.
- I wonder how many days this will continue.
- I wonder how many acorns there are altogether.
Estimation: Prompt
After we have heard students and demonstrated that we value their voice, we can land on the first question we will challenge them with:
The grey squirrel is gathering acorns and burying them in trees or in the ground in preparation for the long winter months. The grey squirrel is a classic example of a scatter hoarder. A scatter hoarder hides food in a bunch of different places within its territory.
If the grey squirrel hoards acorns for ten days, how many acorns will he have?
You might consider replaying the Spark video to give students another opportunity to visualize the number of acorns in the first five days.
We can now ask students to make an estimate (not a guess) as we want them to be as strategic as they can possibly be. This will force them to determine a number of acorns that would be reasonable before determining a more precise answer. Students will likely debate the number of acorns stashed on each day. Discussing whether or not the number was consistently the same. They may also estimate various numbers since it’s difficult to tell how many exactly. Consider asking students to think about a number of acorns that would be “too low” and a number that would be “too high” before asking for their best estimate in order to help them come up with a more reasonable estimate. Encourage students to share their estimates, however avoid sharing their justification just yet. We do not want to rob other students of their thinking.
Estimation: Update & Partial Reveal
Show the following video to students and then ask them to update their estimate:
While students are updating their estimate, listen and observe as students work to make updates. What strategies and mathematical models are students leveraging? Are they:
- Counting by ones?
- Skip counting?
- Repeatedly adding?
- Using known multiplication facts?
- Using a doubling strategy?
Reveal the number of acorns.
Celebrate student estimates that were very close to the actual number of acorns using a routine of your choice as we head into the sense making portion of this lesson.
Fuel Sense-making
Crafting A Productive Struggle: Prompt
Consider sharing the following visual animation to dig deeper into this context:
Here is a script that you can use to prepare for sharing the context with students as the video plays or in place of the video.
Not all squirrels are scatter hoarders. Red squirrels are plain old hoarders. If you’ve ever been walking through the woods and a red squirrel starts screaming at you, it’s defending its one and only stash.
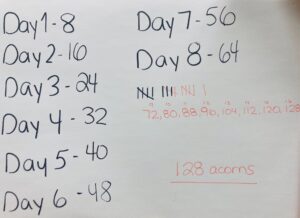
I once observed a red squirrel begin preparing his stash for the winter in a nest in a tree in my yard. At first the nest was empty. On the first day of hoarding, he hid eight acorns in the tree. On the second day, he had 16 acorns altogether. By the third day, there were 24 acorns.
Assuming this squirrel continues hoarding the same number of acorns each day, predict how many acorns he will have at the end of days 4, 5, 6, 7 and 8. How many will he have on day 16?
Be sure to remind students that they are not to use a calculator to determine the number of acorns as using that tool will rob them of this mathematical experience. Students should use a mathematical model in order to communicate their thinking.
During Moves
While Students Are Productively Struggling…
Monitor student thinking by circulating around the room and listening to the mathematical discourse. Select and sequence some of the student solution strategies and ask a student from the selected groups to share with the class from:
- most accessible to least accessible solution strategies and representations;
- most common/frequent to least common/frequent strategies and representations; or,
- choose another approach to selecting and sequencing student work.
The tools and representations you might see students using to convince their peers and/or the teacher include:
- Counting on
- Skip counting by eight
- Repeated addition
- Using doubling strategies and partial products
Have students share their strategies and reasoning for how to represent the number of acorns. Ask them to convince you and their peers that their answer is correct by sharing mathematical models.
Discuss their strategies and elicit student thinking during your consolidation to build off of their current prior knowledge and understanding rather than “fixing” or “funnelling” student thinking to a strategy and/or model that does not connect to their strategy and/or approach.
Student Approaches
Student Approach #1: Counting On
I wrote down the number of acorns on days 1, 2 and 3. I noticed that each time, he adds eight more. So I added 8 more each day by counting, 24… 25, 26, 27, 28. To get to 16 days, I had to count a lot. I used my fingers and tally marks to keep track every time I added eight more.
Student Approach #2: Skip Counting
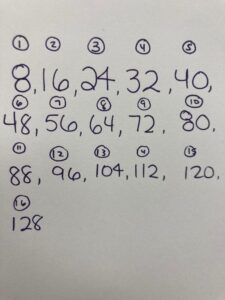
If he adds eight acorns every day, then I can keep counting by 8. I counted by eight and recorded the number of acorns for days 4, 5, 6, 7 and 8… and then I kept counting by eight until I got to 16 days.
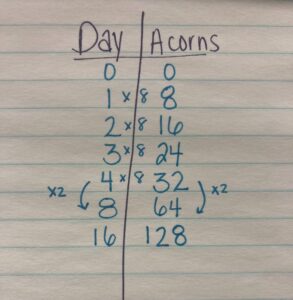
Student Approach #3: Multiplication & Doubling
I know that for every day he collects 8 acorns, I need to multiply by 8. Once I got to 4 days, I doubled the number of acorns for 8 days, I realized that 16 days is twice as many. So I doubled 64 acorns. He collected 128 acorns in 16 days.
Next Moves
Reveal
Show students the following reveal video:
Or, consider sharing the following screenshots from the reveal video:
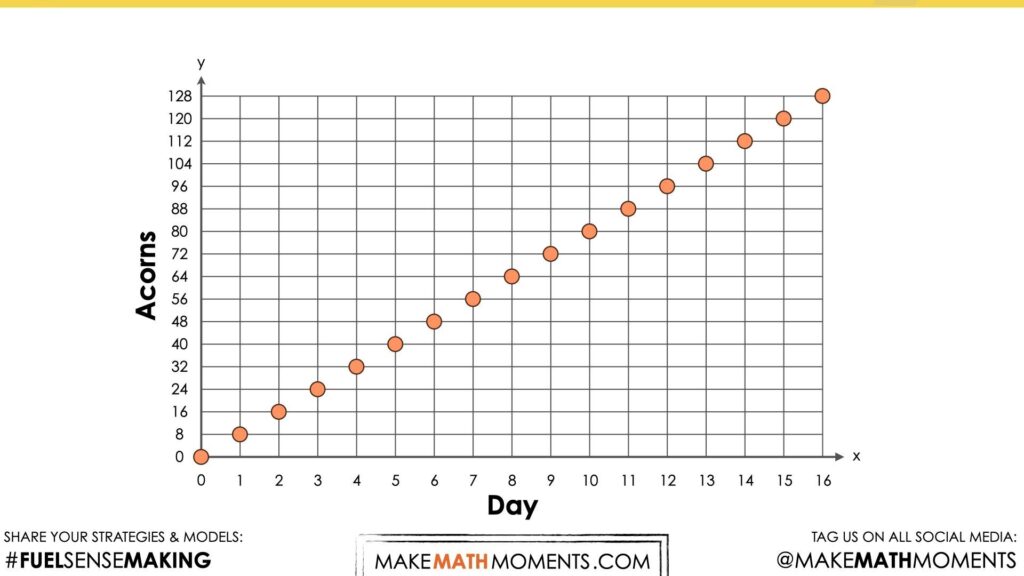
Screenshot #2:
Students will notice that the points of this graph create a straight line that is increasing. Ask them to articulate why they believe that is. Land on the big idea that this is a growing linear pattern, because it increases by the same rate every time.
Facilitator Note: The points in this graph are intentionally not connected. This is in response to the type of data. In the context of the acorns, the data is discrete (not continuous). Each acorn is counted concretely, not measured. In a subsequent unit, Bird Migration, the patterns will reflect continuous, measurable data (distance), and for this reason, the points on the graph will be connected.
Consolidation
Consolidate your intentionally selected student solutions. Look for similarities in students’ approaches along the developmental continuum of counting, to addition and eventually multiplicative thinking.
Consider how students went about extending this pattern and determining the number of acorns on day 16. Encourage students to look for efficiency.
Students likely noticed that this pattern has a constant rate of 8 acorns per day (8 acorns/day).
Ask students the following question:
How would you describe this pattern in words?

Students might be able to articulate that they have to add 8 acorns each time. Others may be able to describe this pattern using multiplicative thinking. Multiply the day by 8 acorns. Help students see both pattern rules in the table of values.
Ask students the following question:
If we were to plot each number in this pattern on a graph (8, 16, 24, 32, 48…), where the x-axis is the number of days, and the y-axis is the number of acorns, what shape will the graph take?
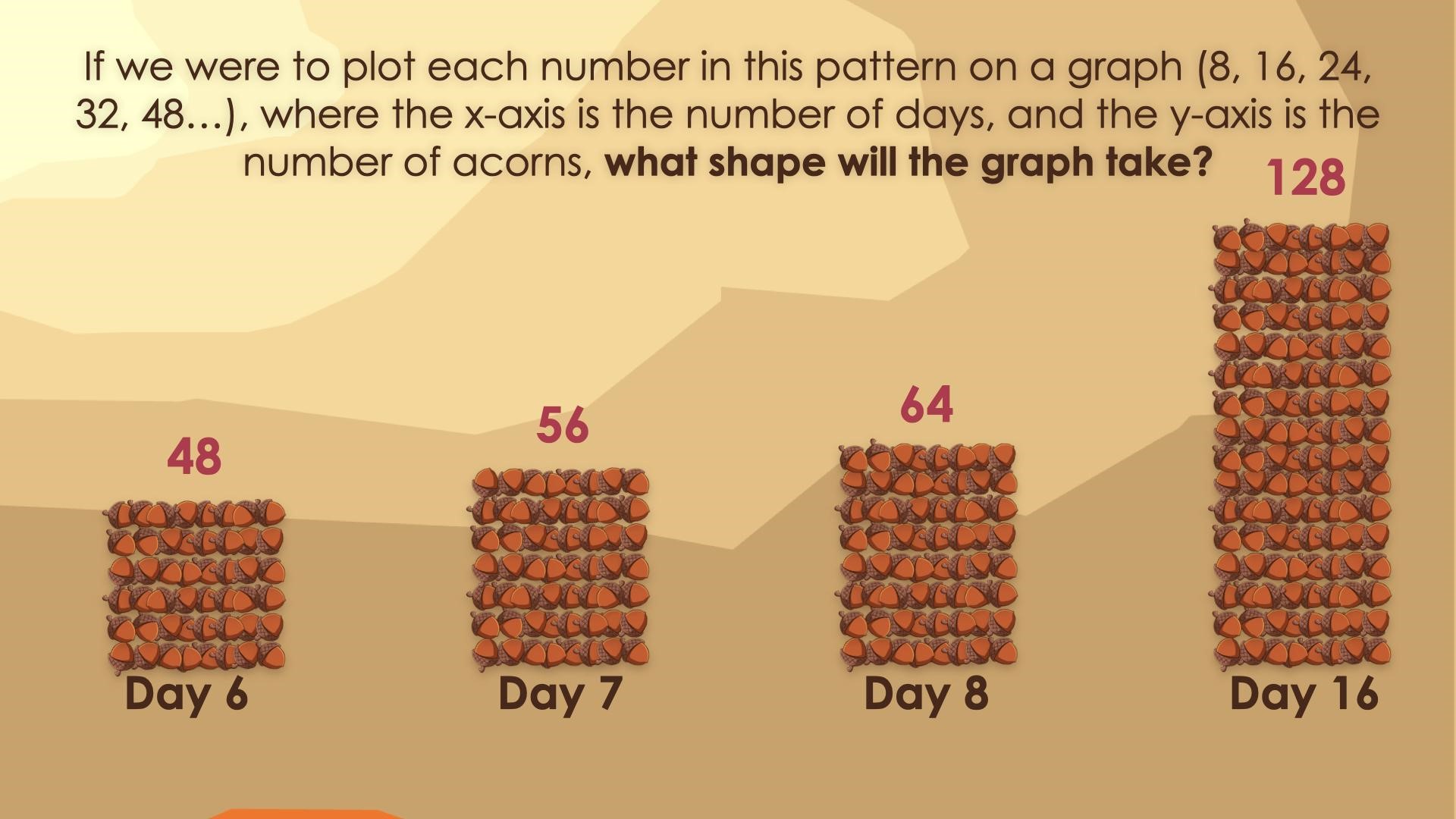
Give students an opportunity to reflect on this question and turn and talk. Allow students the opportunity to share and defend their thinking.
Reflect and Consolidation Prompts
Provide students an opportunity to reflect on their learning by offering these consolidation prompts to be completed independently.
Consolidation Prompt #1:
Today we explored an expression where three (3) is the base and the exponent is the number of weeks. Describe the word base and exponent in this context.
Consolidation Prompt #2:
Consider the pattern below. Describe the pattern rule in words. Extend the pattern to day 5.
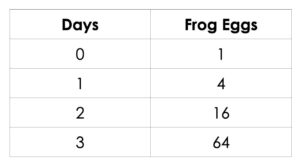
We suggest collecting this reflection as an additional opportunity to engage in the formative assessment process to inform next steps for individual students as well as how the whole class will proceed.
Resources & Downloads
Printable Lesson Plan PDF
Videos, Images & Media Files
Apple Keynote Presentation
Powerpoint Presentation
Printable Consolidation Prompts
Educator Discussion Area
Login/Join to access the entire Teacher Guide, downloadable slide decks and printable handouts for this lesson and all problem based units.
Explore Our 60+ Problem Based Units
This Make Math Moments Lesson was designed to spark curiosity for a multi-day unit of study with built in purposeful practice, number talks and extensions to elicit and emerge strategies and mathematical models.
Dig into our other units of study and view by concept continuum, grade or topic!