CALVIN'S COOKIE COMPANY: BATCHES & BOXES
DEVELOPING PLACE VALUE UNDERSTANDING
Bake in student understanding with this Unit of 3 Act Math Task lessons focused on developing place value understanding
Intentionality
Spark Curiosity
Fuel Sensemaking
During Moves
Student Approaches
Next Moves
Consolidation
Reflect and Consolidation Prompts
Resources & Downloads
Educator Discussion Area
Intentionality & Unit Overview

Length of Unit: 5 Days
Access each lesson from this unit using the navigation links below
Students will determine how many boxes of ten cookies and how many extras can be grouped from a batch of 24 cookies.
Some important vocabulary to use consistently throughout the unit:
Batch: The number of cookies made at one time. A batch of cookies is made from one or more baking sheets.
Baking sheet or sheet: Cookies are baked on sheets in random (non array) arrangements.
Boxes: Cookies are grouped by tens in boxes. All of the cookies in the box are the same flavor. These boxes are for sale to take out of the store.
Trays: Extra cookies are kept on trays. These single cookies are for sale in the store.
Intentionality…
In this task, students will determine how many boxes of ten cookies and how many extras can be grouped from a batch of 24 cookies.
Some of the big ideas that may emerge through this task include:
- Unitizing (10 single cookies can be understood as 1 group of 10 cookies.)
- Place Value Number System (The two digits of a two-digit number represent amounts of tens and ones.)
- Properties of Addition [The commutative a+b=b+a and associative properties (a+b)+c=a+(b+c)]
- Equivalence [through composition and decomposition, a particular quantity can be represented in more than one way
- (22 ones = 1 ten and 12 ones = 2 tens and 2 ones)
- (22 cookies= 1 box and 12 loose cookies = 2 boxes and 2 loose cookies)].
Before starting this unit, students should be familiar with:
- Counting to 100 by ones and by tens.
- Writing numbers from 0 to 100.
- Understanding the relationship between numbers and quantities; connect counting to cardinality.
Spark Curiosity
What Do You Notice? What Do You Wonder?
Show students the following video:
Then, ask students:
What do you notice?
What do you wonder?

Give students about 30-60 seconds to do a rapid write on a piece of paper or silent individual think time.
Replaying the video can be helpful here if appropriate.
Then, ask students to pair share with their neighbours for another 60 seconds.
Finally, allow students to individually share with the entire group. Be sure to write down these noticings and wonderings on the blackboard/whiteboard, chart paper, or some other way that is visible to all. This helps students to see the thinking of their classmates and ensures each student that their voice is acknowledged and appreciated. Adding student names or initials next to their notice/wonder is one way to acknowledge their participation and can motivate others to join in.
Some noticings and wonderings that may come up:
- I wonder what kind of cookies he baked?
- Does Calvin make more than one kind of cookie?
- He took 1 sheet of cookies out of the oven.
- I wonder if all of the cookies on the sheet are the same kind?
- I wonder how many cookies he made in this batch.
- And many more.
At this point, you can answer any noticings and wonderings that you can cross off the list right away. Questions such as “I wonder if all of the cookies are the same kind?” can be addressed right away to show students that we are indeed listening to their contributions and that we value student voice.
Estimation: Prompt
After we have heard students and demonstrated that we value their voice, we can land on today’s question. Acknowledging that the question came from students underscores their identities as thinking mathematicians who are making sense of problems.


How many cookies are in this batch?
Follow up that question with:
How could you convince someone that the quantity you come up with for your estimation is correct?
We can now ask students to make an estimate (not a guess) as we want them to be as strategic as they can possibly be. While you can briefly rerun the video, do not leave the image up for students while they are estimating. This will prevent counting and push students to use their life experience and visual sense of how many cookies are on the try. This will force them to use spatial reasoning such as estimating how many cookies are on the sheet.
Some students may also estimate how many groups of ten are on the baking sheet and add up from that. Before collecting student estimates, students can share their estimates in small groups along with a justification for the reasonableness of their prediction.
Consider asking students to think about a number that would be “too low” and a number that would be “too high” before asking for their best estimate in order to help them come up with a more reasonable estimate.
While Students are Estimating:
Monitor student thinking by circulating around the room and listening to the mathematical discourse. You may identify some students whose thinking would be valuable to share when the group’s estimates are collected.
Encourage students to use precise mathematical language (including tens, ones, extras, groups of ten, greater than, less than, more, less, half, higher than, lower than) to articulate their defense of their estimate. As well, now may be a good time to build up the vocabulary of this context: batch, baking sheet, box, tray.
Similar to collecting their noticings and wonderings, collect students’ range of estimates and/or best estimates along with initials or names. Having some students share justifications is an opportunity for rich, mathematical discourse.
At the end of this task, during The Reveal, revisit the estimates to see how accurate students were and to reflect on the assumptions they held and justifications they argued.
Fuel Sense-making
Crafting A Productive Struggle: Prompt

Since we’ve already invested time to set the context for this problem and student curiosity is already sparked, we have them in a perfect spot to help push their thinking further and fuel sense making.
Ask the students what information they will need and how they will use it in order to find out:
How many cookies are in this batch?
How many boxes can Calvin fill? How many loose cookies will be left over?
Here we are asking students to envision a solution path. By considering what information will be needed and how it can be used to solve the problem, students are being asked to make sense of the problem and reason abstractly and quantitatively (Math Practices 1 and 2). By not simply providing this information, we are inducing students to engage more deeply with the problem and think about all of its parts, known and unknown, before they begin crunching the numbers.
After they have requested information and explained how they would use it to solve the problem, the following information can be provided.
- A picture of the 24 chocolate chip cookies randomly arranged on the baking sheet.
- An empty Calvin’s Chocolate Chip Cookies box with the label on the side clearly showing that it can hold 10 cookies. (The 10 cookie capacity was not visible in the video).
During Moves
While Students Are Productively Struggling…
Monitor student thinking by circulating around the room and listening to the mathematical discourse. At this time, teachers are looking for clear representations of student thinking to display later during the whole class discourse. In order to have a rich discussion later in the task, it is vital that teachers are intentional when they select a few work samples to share.
As students work to find out how many boxes can be filled, how many extras will be on the tray, and how many cookies there are all together in this batch, teachers can use some of their time to guide students who are struggling towards tools that might help them move forward towards a solution. Throughout this unit 10 frames and Base 10 notation{ ⎢ , ⌑ } might be tools that could help students with unitizing in groups of ten.
However, during the majority of the student working time, it is essential for teachers to thoughtfully select some of the student solution strategies. After making a selection, ask a student from the group if they will be willing to present the group’s thinking during the whole class discourse.
Teachers should then sequence these work samples in a way that structures the discourse. Some possible ways to sequence the work samples include:
- Most accessible to least accessible solution strategies and representations.
- More common/frequent to less common/frequent strategies and representations.
- From concrete to pictorial to symbolic representations.
- Side by side simultaneous views that can highlight one key difference that is essential to finding a solution.
- Choose another approach to selecting and sequencing student work.
The tools and representations you might see students using to convince their peers and/or the teacher include:
- Using a tool to count out each of the 24 cookies and then group them in ten with some type of barrier such as a string or a ruler.
- Making 24 marks (ie: tallies, circles, exes, etc) and counting all of them. Then circling groups of ten.
- Circle groups of 10 cookies. Skip count 10, 20. Then add on the final cookies one at a time (10, 20, 21, 22, 23, 24).
- Represent the 24 with Base 10 block drawing representing the cookies in groups of ten and some ones { ⎢ , ⌑ }. Then add or count by tens and then the ones.
- Starting with the equation 10+10+4=?. Then adding 10+10=20. Then, combining the partial sums 20+4=24. Or start with 24 and subtract groups of ten when moving cookies from the baking sheet to a box.
Student Approaches
Student Approach #1: Counting All with a Tool
I counted out 24 stackers for the 24 cookies. Then I found 10 cookies and put them in one box. Then I found 10 more cookies and put them in another box. There were 4 extras left over. So, there are two boxes and 4 extra cookies.
Student Approach #2: Counting All with a Drawing
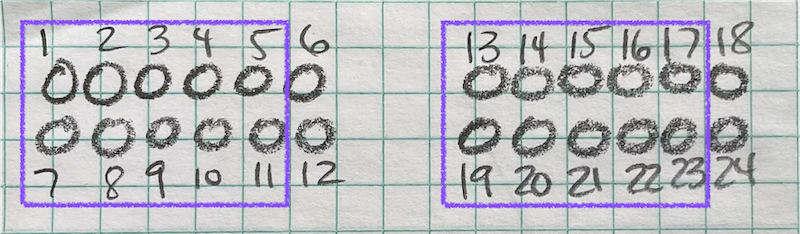
I drew 24 circles for the 24 cookies. Then I drew a box around two groups of ten cookies. That’s 2 boxes with 4 extras to sell in the store.
Student Approach #3: Grouping and Skip Counting/Repeated Addition
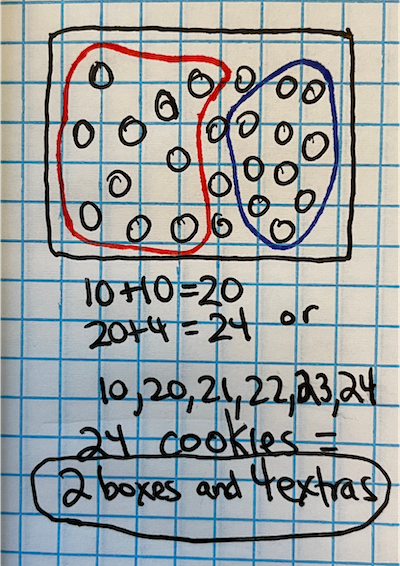
I drew all 24 cookies. Then I circled two groups of ten cookies. There were 4 extra cookies. That’s 10, 20, 21, 22, 23, 24. My partner knew it was 24 because 10+10=20 and 20+4=24.
So, we think it’s 2 boxes of ten and 4 extra cookies.
Student Approach #4: Base 10 Block Drawing to Represent Skip Counting
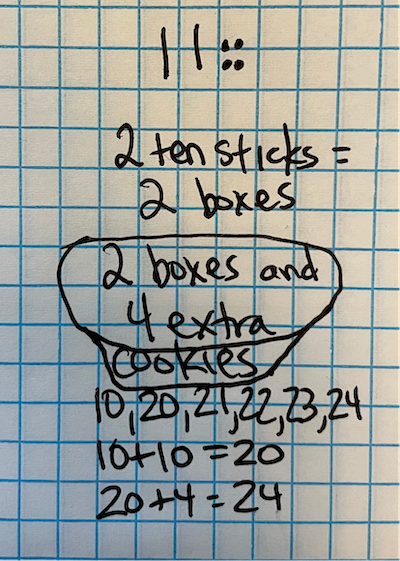
I know 24 is made of 2 tens and 4 ones. So I drew 2 ten sticks and 4 ones to show it. Each ten stick is a box. So, the 24 cookies can go in 2 boxes with 4 extras.
Student Approach #5: Equations to Represent a Represent Skip Counting or Adding by Place
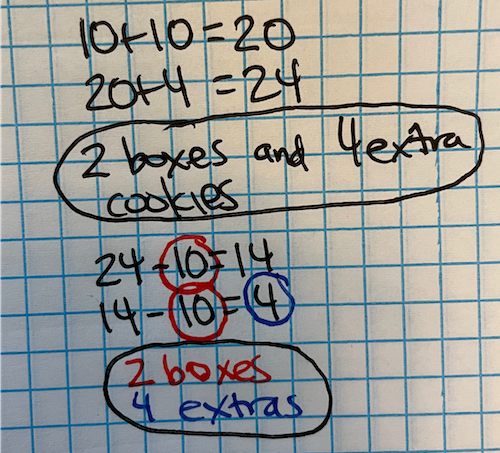
Partner #1: I know 24=10+10+4. So that is two boxes of ten cookies and 4 extras to keep on the tray to sell in the store.
Partner#2: I thought about the 24 cookies on the baking sheet. I took 10 cookies to put in one box. That left 14 cookies on the sheet. Then I put another 10 cookies in another box. That left 4 cookies to put in the tray. So, it’s 2 boxes and 4 extras.
Next Moves
Reveal
Show students the following reveal video:

Consolidation
Consolidate learning by facilitating a student discussion.
Have a few students present their work one by one or group by group according to the sequence that the teacher determined during the Sense Making portion of the lesson. During student presentations, the teacher can promote discussion by facilitating commenting and question asking between classmates. The twin goals of discussion are to get students to engage one another and to think about how groups of 10 (unitizing) can help when counting or adding within 100.
To promote student engagement and facilitate discussion, teachers can:
- Create a psychologically safe space to promote intellectual risk taking, new ideas, and broader participation during discussions,
- Providing guided practice in advance regarding how to present work, appropriate voice volume, how to listen, how to agree/disagree respectfully, and other behaviors and practices to promote discussion.
- Make student work easily visible by using a document camera or other tool so that the image is large.
- When an important point is made by a student, prompting other students to repeat/rephrase it. This encourages listening to one another and allows for an important point to be stated 2-3 times so that more people can hear it.
- Instead of answering questions asked by students, redirecting the question back to the class. This promotes student to student dialogue.
- While it is important to keep the consolidation purpose in mind, also being open to other important thoughts and ideas that arise. Honoring these rich insights builds excitement and students’ vision of themselves as mathematicians making discoveries.
To promote greater understanding of place value thinking, teachers can:
- Familiarize themselves with the place value thinking teaching points below each Student Approach. As students explain their thinking during the class discussion, listen for and highlight their explanations and representations that demonstrate unitizing ten cookies into a box of ten (place value understanding). Or better yet, have a classmate rephrase the approach of the presenting group. By guiding the discussion in this direction, teachers will help their class to construct their own understanding of using place value thinking to count large numbers of objects.
- Ask questions such as,
- How many cookies are in each box?
- How can we show that in a drawing or diagram?
- How is counting all of the cookies by ones different from counting by boxes of ten plus the extras?
- How can the boxes of 10 cookies help us figure out the total number of cookies?
- What about the extra cookies on the tray?
Have students present their strategies and reasoning for how they counted or added up the 24 cookies. Ask them to convince you and their classmates that their answer is correct by sharing their mathematical model. It is essential to project the student work with a document camera or project a photo of the student work from your computer so that everyone can easily see what the presenting student is referring to. When the other students can easily see the work sample, they remain more engaged and understand more deeply.
Discuss student strategies and elicit the questions and comments of other students during your consolidation. The goal is to help them to build off of their current prior knowledge and understanding. We want students to be socially constructing their understanding in a way that makes sense for them.
Here you are listening to this discourse with an ear for what is important for your students’ emerging understanding of unitizing and understanding 10 more and 10 less than.
Reflect and Consolidation Prompts
After the reveal, check back to your estimations. The purpose here is to reflect on student reasoning, not on celebrating who was closest.
Were there some estimates in the right neighborhood?
What helped those students to get close?
How did they think about it?
Without a lot of information, mathematicians have to make assumptions all of the time. What assumptions made some estimates way too low or way too high?
Now that we have figured out how many cookies were in this batch, what new questions does this raise in your mind? You may choose to explore one of more of these student generated questions on another day or as homework.
Provide students an opportunity to reflect on their learning by offering these consolidation prompts to be completed independently.
Consolidation Prompt #1:
Calvin made a new batch of peanut butter cookies. There were two baking sheets in the batch. There were 8 peanut butter cookies on each baking sheet.
How many boxes could Calvin fill?
How many peanut butter cookies is that?
Show your thinking with equations and a drawing.
Consolidation Prompt #2:
For a party Calvin baked 3 baking sheets of chocolate chip cookies. Each sheet had 12 cookies.
How many cookies did Calvin bake for the party?
Show your thinking with equations and a drawing.
Consolidation Prompt #3:
At Calvin’s bakery, there were 56 sugar cookies on the baking sheet.
Can you think of more than one way for him to organize them into boxes of 10 and extras on the tray? Can you find all the ways?
How many cookies are there altogether?
Show your thinking with equations and a drawing.
Consolidation Prompt #4:
Write a story about Calvin baking a batch of your favorite kind of cookies and filling 3 boxes of cookies and having 2 loose cookies on the display tray.
We suggest collecting this reflection as an additional opportunity to engage in the formative assessment process to inform next steps for individual students as well as how the whole class will proceed.
Resources & Downloads
Printable Lesson Plan PDF
Videos, Images & Media Files
Apple Keynote Presentation
Powerpoint Presentation
Printable Consolidation Prompts
Educator Discussion Area
Login/Join to access the entire Teacher Guide, downloadable slide decks and printable handouts for this lesson and all problem based units.
Explore Our 60+ Problem Based Units
This Make Math Moments Lesson was designed to spark curiosity for a multi-day unit of study with built in purposeful practice, number talks and extensions to elicit and emerge strategies and mathematical models.
Dig into our other units of study and view by concept continuum, grade or topic!



