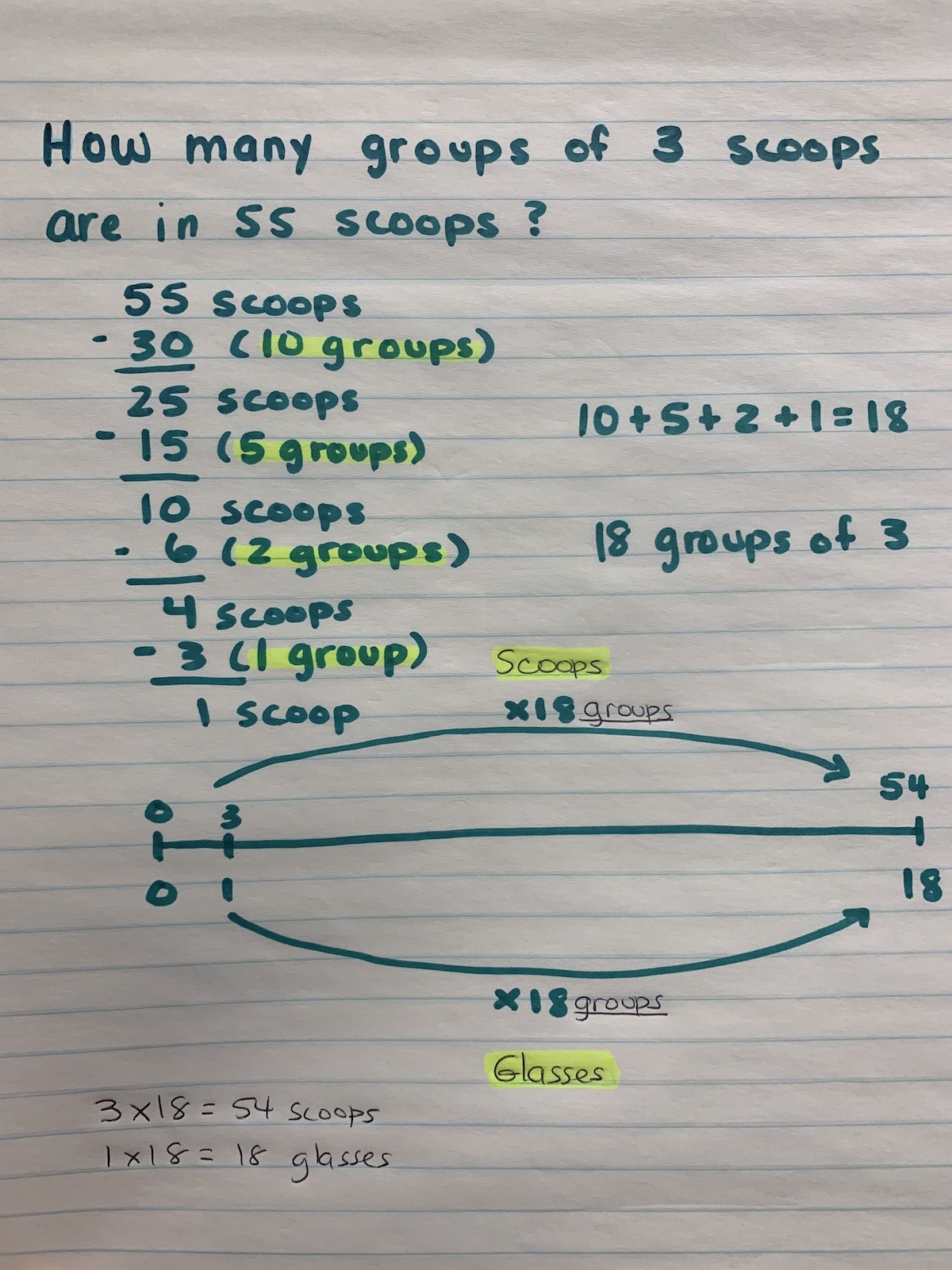HOT CHOCOLATE
MULTIPLICATION & PROPORTIONAL REASONING
Explore proportional relationships through skip counting, repeated addition, multiplication, and more.
Intentionality
Spark Curiosity
Fuel Sensemaking
During Moves
Student Approaches
Next Moves
Consolidation
Reflect and Consolidation Prompts
Extend
Resources & Downloads
Educator Discussion Area
Intentionality & Unit Overview

Length of Unit: 6 Days
Access each lesson from this unit using the navigation links below
Students will explore the idea of scaling in tandem with a ratio as a composed unit.
Intentionality…
In this task, students will have an opportunity to reason through an activity involving the ratio between two quantities; scoops of hot chocolate and glasses of hot chocolate. Through this task, students will have the opportunity to apply models including the double number line and the ratio table. They will also explore big ideas including the following:
- Unitizing;
- Ratio reasoning through scaling in tandem;
- The relationship between repeated addition and multiplication;
- The relationship between multiplication and division, particularly quotative division; and,
- A composed unit is one way of defining the relationship that exists in a ratio.
Spark Curiosity
What Do You Notice? What Do You Wonder?
Show students the video below showing a can of hot chocolate mix being placed on the counter. Ask students to engage in a notice and wonder protocol. ANYTHING and EVERYTHING that comes to mind is fair game.
Write down all of the student noticing and wondering. For example:
Ask students to engage in a notice and wonder protocol. ANYTHING and EVERYTHING that comes to mind is fair game.
Write down all of the student noticing and wondering. For example:
- I notice hot chocolate.
- I notice a glass.
- I wonder if the hot chocolate is already made in the container?
- I wonder if someone is making hot chocolate?
- I wonder if that is YOU in the video.
- And many others…
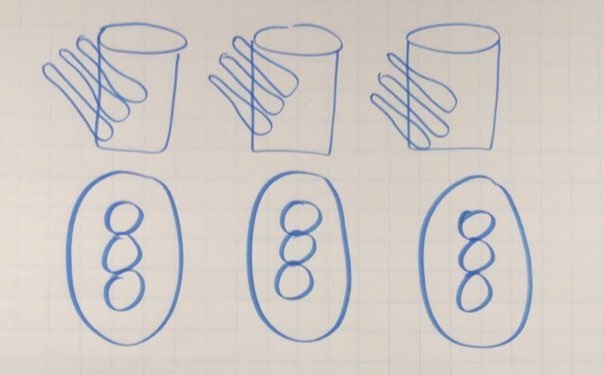
- I saw him place 9 scoops in the glass.
- Why is he putting hot chocolate mix in a glass and not a mug?
- How many scoops in total are in the container?
- And many others…
Fuel Sense-making
Crafting A Productive Struggle: Prompt
Then, pose the following question:
How many scoops will he need to make 8 glasses of hot chocolate?
Follow up that question with:
How might we convince someone that the quantity you come up with is correct without the use of a calculator?
Let them loose to make some estimates based on what they saw.
During Moves
While Students Are Productively Struggling…
Monitor student thinking by circulating around the room and listening to the mathematical discourse. Select and sequence some of the student solution strategies and ask a student from the selected groups to share with the class from:
- most accessible to least accessible solution strategies and representations;
- most common/frequent to least common/frequent strategies and representations; or,
- choose another approach to selecting and sequencing student work.
The tools and representations you might see students using to convince their peers and/or the teacher include:
- Pictures/pictorial representations of glasses and spoons.
- Set model using counters, cubes, or other manipulatives to represent the number of scoops. Possibly drawing circles around the concrete materials to represent each glass.
- Linking connecting cubes, representing 3 scoops and 1 glass at the same time.
- Symbolic representation (i.e.: 8 x 3 = 24 or 3 + 3 + 3 + 3 + 3 + 3 + 3 + 3 = 24).
- Double number line and/or ratio table.
- As well as others…
Have students share their strategies and reasoning for determining the number of scoops of hot chocolate to make 8 glasses.
Ask them to convince you and their peers that their answer is correct by sharing mathematical models.
Discuss their strategies and elicit student thinking during your consolidation to build off of their current prior knowledge and understanding rather than “fixing” or “funnelling” student thinking to a strategy and/or model that does not connect to their strategy and/or approach.
Student Approaches
Student Approach #1: One-to-One Counting
I started by drawing the cups with the spoonfuls, but realized that was going to take me a long time.
So instead, I drew large circles to represent the glasses with 3 smaller circles inside to represent each scoop.
I am going to draw 5 more large circles with 3 smaller circles in each one. Then, I’ll count up all of the small circles to determine the total number of scoops.
Strategy
Accessing multiplication through a one-to-one counting strategy.
Student Approach #2: Skip Counting
I used connecting cubes to represent both the number of scoops and number of glasses.
I used 3 cubes of 1 colour to represent the 3 scoops per 1 glass of hot chocolate.
I then skip counted by 3s to find the total of 24 scoops.
Big Ideas
This student demonstrates an ability to apply the big idea of unitizing by redefining her unit as 3 scoops (instead of a single scoop) and counting by 3 cubes.
Another big idea revealed through this model is ratio reasoning because the student iterates multiple copies of 1 glass and 3 scoops in tandem. Because the student scales both quantities in tandem (i.e.: as one unit), the idea of thinking of a ratio as a composed unit is emerging.
Strategy
Skip counting by units of 3.
Student Approach #3: Scaling, Then Additive
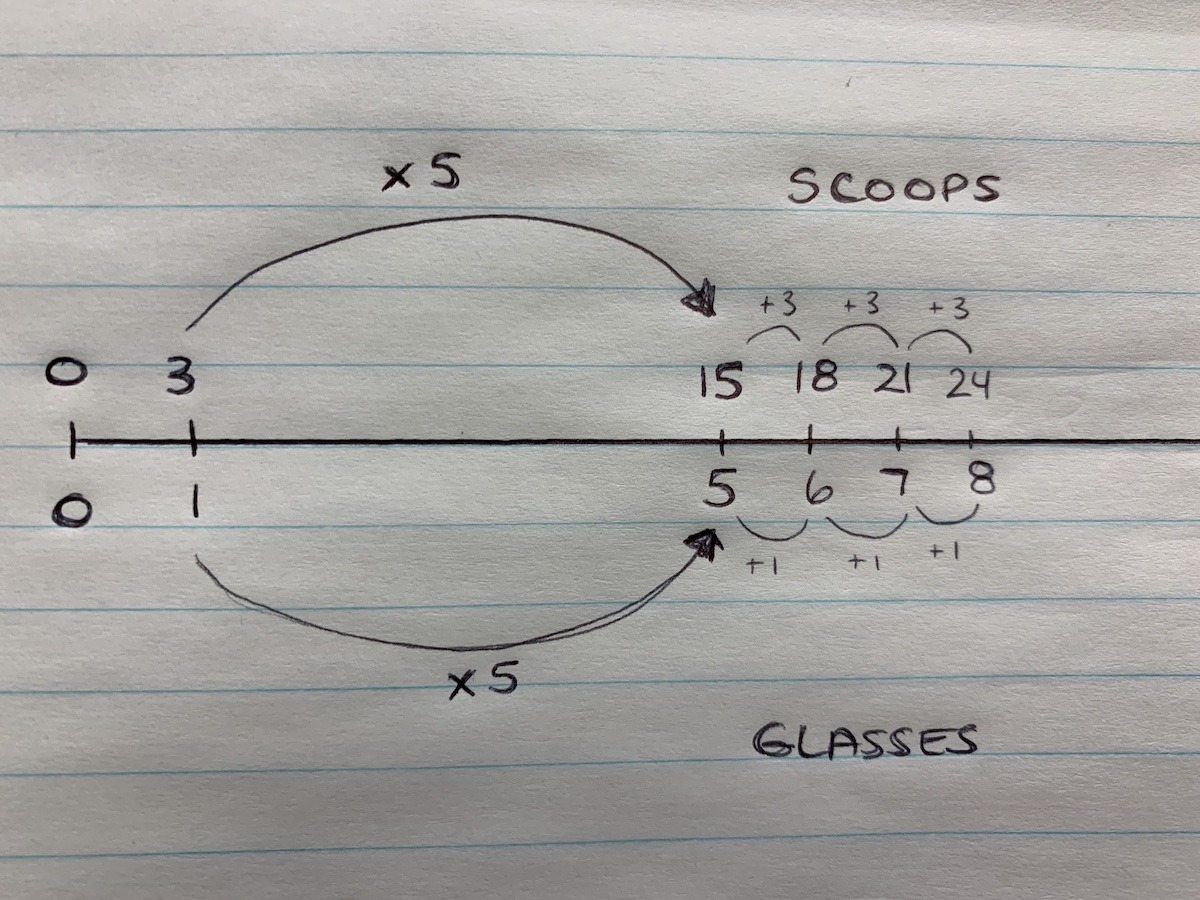
I made a double number line starting at 3 scoops and 1 glass, then multiplied by 5 to 15 scoops and 5 glasses.
Then, I added 3 scoops and 1 glass three more times to get to 24 scoops and 8 glasses.
Big Ideas
This student used their understanding of ratio reasoning by scaling both quantities in tandem (i.e.: as one unit) while thinking of the ratio as a composed unit.
Strategy
This student used known facts by scaling both quantities in tandem by a scale factor of 5, then used repeated addition to add units of 3 scoops and 1 glass until reaching 24 scoops and 8 glasses.
Student Approach #4: Multiplication Using Known Facts
I multiplied the number of glasses and the number of scoops by 8 in my ratio table.
Big Ideas
This student used their understanding of ratio reasoning by scaling both quantities in tandem (i.e.: as one unit) while thinking of the ratio as a composed unit.
Strategy
This student used known facts to multiply both quantities in the ratio by 8.
Facilitator Notes
This strategy demonstrates why setting up and solving a proportion using ratio reasoning (or rate reasoning) is an efficient way to find an unknown quantity within a proportional relationship.
Students should be encouraged to explore ratio and rate reasoning through mathematical models such as the double number line and ratio table before jumping to procedures such as setting up a proportion of equivalent rates.
Next Moves
Reveal
After consolidating learning using student generated solution strategies and by extending their thinking intentionally, we can share what really happened by showing the video revealing how many scoops for 3 glasses, followed by an image showing how many scoops for 8 glasses:
Alternatively or in addition to the video, you can show the still image below.
Answer: 24 scoops of hot chocolate mix.
Revisit the student answers.
Consolidation
Consolidate learning using student generated solution strategies based on what you selected and how you sequenced while monitoring during the Sense Making portion of the lesson.
The purpose of the consolidation is to make connections between strategies and reveal and/or solidify big ideas.
In particular, highlighting how the double number line model helps us to better understand the behaviours of a ratio that is being treated as a composed unit (i.e.: quantities in a ratio being thought of as a single unit).
In this example, students should be able to clearly articulate why both the glasses and number of scoops were multiplied by the same scale factor to reveal an equivalent ratio from the proportional relationship.
You may consider officially namingthis idea as scaling in tandem.
Reflect and Consolidation Prompts
Provide students an opportunity to reflect on their learning by offering this consolidation prompt to be completed independently.
Consolidation Prompt:
One student claims that they could determine the number of scoops in 8 glasses by doubling the number of glasses from 1 glass to 2 glasses, then from 2 glasses to 4 glasses, and finally doubling from 4 glasses to 8 glasses.
What must this student do to the number of scoops in order to see this strategy through?
Share another clever strategy you might use to determine the number of scoops for 10 glasses.
We suggest collecting this reflection as an additional opportunity to engage in the formative assessment process to inform next steps for individual students as well as how the whole class will proceed.
Extend
Crafting A Productive Struggle: Extension Prompt
Share the EXTEND: PROMPT question:
How many glasses of hot chocolate can be made with 55 scoops of mix?
Intentionality…
This task can be used to explore one of the two types of division; in this case, quotative division.
Some of the big ideas that can be deepened from the first portion of this lesson and newly emerged through this task include:
- Ratio reasoning: the idea that a ratio can be thought of as a composed unit and can be scaled in tandem;
- Quotative division can be used to reveal a scale factor (i.e.: how many groups of one quantity are in another of the same unit).
Student Approach #1: Multiplication With Known Facts, Then Repeated Addition
I know that 1 glass has 3 scoops, so 10 glasses must have 30 scoops.
That wasn’t enough scoops, so I kept counting by 1 glass and 3 scoops each time until I got to 54 scoops and 18 glasses.
I knew that more glasses would be too many scoops, so the answer is 18 glasses with 1 scoop left over.
Strategy:
Student used known facts to scale by a factor of 10 to 30 scoops and 10 glasses. Then, the student used repeated addition until arriving at 54 scoops and 18 glasses with 1 scoop remaining.
Student Approach #2: Doubling, Then Partitioning
I already had my ratio table drawn for the first question and knew that there were 24 scoops in 8 glasses.
So, I doubled both the number of scoops and number of glasses to get 48 scoops and 16 glasses.
Since I was close, I knew that I could add 2 glasses and 6 scoops to get me to 54 scoops and 16 glasses.
I had 1 scoop leftover, but my teacher asked me how much of a glass that scoop represented. So I drew this picture over here (points to bar model in bottom right).
Big Ideas:
Units can be composed and decomposed. For example, this student composed a new unit by combining 2 glasses for a single unit of 6 scoops. Also, this student decomposed 1 glass into equal parts by partitioning 1 whole glass into 3 thirds of a glass.
Strategy:
Student used a doubling strategy to scale by a factor of 2. Then, made a new unit of 2 glasses and 6 scoops to add. Finally, the student partitioned one glass into 3 parts to determine the fractional number of glasses for 1 scoop.
Student Approach #3: Flexible Division Using Repeated Subtraction
I knew I had to figure out how many groups of 3 scoops were in 55 scoops, so I kept trying to subtract as many groups of 3 as I could at a time.
First, I subtracted 10 glasses of 3 scoops (or 30 scoops) and had 25 scoops remaining.
I knew 5 groups of 3 glasses is 15 scoops, so that left me with 10 scoops remaining.
Then, I removed 2 more glasses of 3 scoops leaving me with 4 scoops left.
So I can remove 1 more glass of 3 scoops, leaving 1 scoop leftover.
I drew a double number line to prove that it works.
Big Ideas:
Although this student may not realize it, they are emerging the big idea that quotative division can reveal the multiplicative comparison (or scale factor) between two quantities of the same unit.
Strategy:
The student approached quotative division through repeated subtraction. Instead of subtracting 3 scoops at a time, the student used known facts to subtract combined groups of 3 scoops (unitizing) to be more efficient.
Consolidation
Consolidate learning using student generated solution strategies based on what you selected and how you sequenced while monitoring during the Sense Making portion of the lesson.
In particular, highlighting how despite the fact that some students may choose to scale the composed unit of 1 glass to 3 scoops in various methods (i.e.: using repeated addition, scaling in tandem, etc.) all the way to 18 and ⅓ glasses and 55 scoops, the number of glasses can also be revealed by dividing the number of total scoops (55 scoops) by the rate (3 scoops per glass) to reveal a scale factor of 18 and ⅓.
This is an example of quotative division (i.e.: knowing the rate or “quota” and determining the number of iterations or “parts” of that rate that compose the total number of scoops).
Reveal
After using student generated solutions to make connections, you can reveal this image.
ANSWER: 18 ⅓ glasses
Reflect
Provide students an opportunity to reflect on their learning by offering this consolidation prompt to be completed independently.
Consolidation Prompt #1:
Your relative claims that with 16 scoops of hot chocolate mix, we can make 5 and ⅓ glasses of hot chocolate.
Using division and a model to represent your thinking, convince us whether your relatives claim is true or not.
Consolidation Prompt #2:
One student claims that they could determine the number of scoops in 8 glasses by doubling the number of glasses from 1 glass to 2 glasses, then from 2 glasses to 4 glasses, and finally doubling from 4 glasses to 8 glasses.
What must this student do to the number of scoops in order to see this strategy through?
Share another clever strategy you might use to determine the number of scoops for 10 glasses.
We suggest collecting this reflection as an additional opportunity to engage in the formative assessment process to inform next steps for individual students as well as how the whole class will proceed.
Resources & Downloads
Printable Lesson Plan PDF
Videos, Images & Media Files
Apple Keynote Presentation
Powerpoint Presentation
Printable Consolidation Prompts
Educator Discussion Area
Login/Join to access the entire Teacher Guide, downloadable slide decks and printable handouts for this lesson and all problem based units.
Explore Our 60+ Problem Based Units
This Make Math Moments Lesson was designed to spark curiosity for a multi-day unit of study with built in purposeful practice, number talks and extensions to elicit and emerge strategies and mathematical models.
Dig into our other units of study and view by concept continuum, grade or topic!